В 1950-х гг. в России академики Л.И. Мандельштам и Н.Д. Папалекси [1] проводили исследования физических свойств электрического колебательного контура, в котором применялся воздушный конденсатор переменной ёмкости. У конденсатора одна из обкладок была неподвижна, а вторая, с радиальными прорезями, вращалась с постоянной угловой скоростью электродвигателем, частоту вращения которого можно было изменять.
Как показали эксперименты, механическое изменение ёмкости в последовательном контуре без источника питания всегда приводило к тому, что на обкладках конденсатора накапливался избыточный электрический заряд.
На наш взгляд, они обнаружили неизвестную ранее в физике механо-элекрическую систему, в которой происходило циклическое преобразование механической энергии, поступающей извне в электроёмкость, в электрическую энергию колебаний контура.
Представляет интерес выяснить, какие классы периодических электрических колебаний существуют в последовательном колебательном контуре без источника тока, но с гармонической модуляцией реактивного параметра.
Ниже проведено численное моделирование решений обыкновенного линейного дифференциального уравнения второго порядка, описывающего эти процессы. Моделирование показывает, что в зависимости от значения добротности контура уравнение имеет три класса решений: затухающие периодические колебания, параметрический резонанс и решения с токовой неустойчивостью.
Дифференциальное уравнение задачи
Получим дифференциальное уравнение, из которого следуют три класса решений для схемы без источника питания, представленной на рис. 1. Накачка энергии в контур происходит через механическое гармоническое изменение ёмкости.
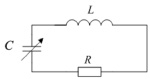
Рис. 1. Включение элементов исследуемой электрической цепи
Если в такой схеме возникают периодические колебания, то в любой момент времени сумма переменных напряжений в контуре равна нулю
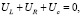(1)
где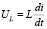 
– напряжение на индуктивности; 
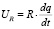– напряжение на активном сопротивлении (закон Ома); 
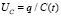– напряжение на емкости. Переменный ток и заряд связаны соотношением 
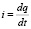. Под активным сопротивлением R контура в (1) понимается его суммарное значение, в которое входит омическое сопротивление реальной индуктивности, омические сопротивления соединений и омическое сопротивление ёмкости, обусловленное воздушным диэлектриком.
Предположим, что закон изменения ёмкости во времени имеет гармонический вид
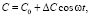(2)
где w – частота её изменения, t – время, DС – амплитуда модуляции ёмкости, С0 – невозмущённое значение ёмкости. Введём безразмерный параметр g приведённой амплитуды модуляции ёмкости относительно её невозмущённого значения
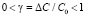. (3)
Выразим все напряжения через заряд и его производные и подставим в уравнение (1):
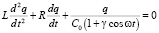. (4)
Разделив обе части (4) на L, получим точное уравнение периодических колебаний заряда в контуре при наличии гармонического изменения одного из реактивных параметров
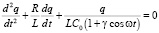. (5)
В уравнении (5) перейдём к безразмерным переменным. Введём функцию приведённого заряда y = q(x)/q0, где q0 – масштаб заряда. Под переменной x будем понимать приведённое время, которое связано с собственной частотой контура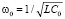 
, настроенного на невозмущённую ёмкость. Переменная x имеет различные представления
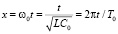, (6)
где T0 – собственный период колебаний контура. Тогда уравнение (5) примет окончательный вид
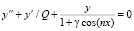. (7)
Заметим, что похожая структура интегро-дифференциального уравнения для негармонического изменения ёмкости была предложена в [1], но численное моделирование его не проводилось.
Решения уравнения (7) зависят от безразмерных параметров: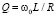 
– добротность колебательного контура, g – параметр приведённой амплитуды модуляции ёмкости; 
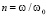– отношение частоты гармонического изменения реактивного параметра к резонансной частоте контура; начальный приведённый стартовый ток электрической цепи 
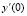и накопленный на ёмкости приведённый начальный заряд y(0).
Структура уравнения (7) не встречается в математических справочниках [2]. Подстановка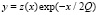 
приводит его к уравнению Хилла относительно функции z(x) (2.30 на с. 374 в [2]): 
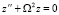(дифференцирование по времени t) c собственной частотой 
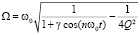, зависящей от параметров 
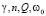и времени t. Каноническое уравнение Хилла для смещения z(x) описывает уникальную колебательную систему, в которой обобщённая «жесткость» пружинного маятника с единичной массой зависит от двух конкурирующих факторов: статической диссипации системы 
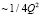и динамической раскачки периодической возвращающей «силой» 
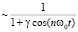. Фактор динамической раскачки колебаний зависит от отношения 
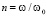и имеет оптимальное значение 
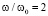(параметрический резонанс). Для такой механической аналогии при γ = 0 (раскачка колебаний отсутствует) и 
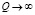(диссипации в системе нет) уравнение переходит в уравнение гармонических колебаний с частотой 
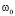. Закон сохранения механической энергии маятника выполняется. При γ = 0 (раскачки нет) и изменении Q в пределах 
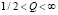система чисто диссипативная и уравнение описывает только затухающие колебания. Закона сохранения механической энергии нет.
В общем случае 0 < γ < 1 периодические колебания в контуре с диссипацией происходят под действием возвращающей «силы раскачки», зависящей от времени и координаты. Энергия контура не сохраняется и может иметь вид убывающих или нарастающих во времени колебаний на переменной частоте, близкой к резонансу. Работа внешней переменной силы непрерывно изменяет энергию контура. Скорость изменения полной энергии в контуре определяют скорости изменения факторов диссипации и раскачки.
Пример похожей периодической раскачки механических колебаний в гравитационном поле: физический маятник в среде с вязким трением, у которого гармонически изменяется длина подвеса. Длительный процесс передачи энергии может перевести финитные по углу колебания маятника в инфинитные. Тогда его угловая скорость будет увеличиваться до бесконечности.
Будем решать уравнение (8) численным моделированием по схеме Рунге – Кутты четвёртого порядка с удвоенной точностью для восьми периодов основного колебания. При моделировании будем считать, что относительная модуляция ёмкости составляет либо 20 % (g = 0,2), либо 80 % (g = 0,8), затравочный заряд на конденсаторе либо равен нулю y(0) = 0 (для переменной заряда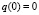 
), либо имеет начальное значение, равное масштабу заряда 
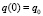. При этом для первого класса начальных условий стартовый ток всегда один и тот же 
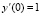(для переменной заряда 
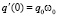). Для второго класса начальных условий стартовый ток будем считать равным нулю 
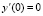, а начальное значение заряда – совпадающим с его масштабом y(0) = 1.
Затухающие колебания в низкодобротном контуре
Как показывает численное моделирование (8), в низкодобротном контуре могут существовать затухающие периодические колебания. На рис. 2 представлены зависимости от времени двух процессов: процесса затухающих периодических колебаний в нижней части графика и процесса зависимости от времени ёмкости в верхней части графика.
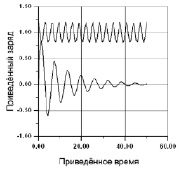
Рис. 2. Затухающие колебания контура при низкой добротности
Для рис. 2 расчёты выполнены для следующих значений параметров: добротность контура – Q = 4; отношение частот n = 2 (параметрический резонанс Мандельштама – Папалекси [1]); процент модуляции емкости – 20 % (g = 0,2); 16 – периодов колебаний раскачки; 8 – периодов затухающих колебаний. Отношение амплитуд для первых двух периодов колебаний равно ~2. Нижний график указывает на наличие затухания при низкой добротности контура (преобладание диссипации над раскачкой колебаний). Похожие решения получаются и для второй комбинации начальных условий.
Параметрический резонанс в контуре со средней добротностью
Как показывает численное моделирование, в контуре со средней добротностью при параметрическом резонансе могут существовать незатухающие периодические биения заряда. На рис. 3 представлены зависимости от времени двух процессов: процесса параметрических биений в нижней части графика и процесса зависимости от времени ёмкости в верхней части графика.
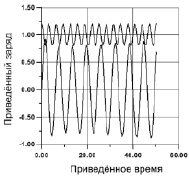
Рис. 3. Режим периодических биений заряда в контуре на параметрическом резонансе
Расчёты для рис. 3 выполнены для следующих значений параметров: добротность контура – Q = 10,53; те же начальные условия. Отношение частот n равно 2 (параметрический резонанс). Процент модуляции емкости – 20 %. 16 периодов колебаний раскачки. 8,5 периодов биений с экстремальными значениями приведённого заряда, заключёнными в диапазоне от –0,8 до +0,8. В системе факторы диссипации и раскачки колебаний компенсируют друг друга. Впервые параметрический резонанс обнаружен в [1].
Токовая неустойчивость в контуре с высокой добротностью
В контуре с высокой добротностью может существовать режим раскачки периодических колебаний заряда, возникающий за счёт проявления токовой неустойчивости колебательного контура. В этом случае фактор раскачки колебаний оказывается больше фактора диссипации.
На рис. 4 представлены зависимости от времени процесса раскачки периодических колебаний заряда и процесса зависимости от времени ёмкости. Расчёты для рис. 4 выполнены при следующих параметрах: добротность – Q = 100. Отношение частот n = 2. Процент модуляции емкости g – 20 %. Выбран первый набор начальных условий. Результат: 16 периодов колебаний раскачки, 8,5 периодов нарастающих колебаний. Для этих значений амплитуда заряда в контуре для второго граничного условия увеличивается в 6 раз. Для значения параметра приведённой амплитуды изменения ёмкости в 80 %, на том же количестве периодов, амплитуда зарядов в контуре возрастает более чем в 10 000 раз (на рис. 4 не показана). Электрическую энергию в контур непрерывно поставляет фактор динамической раскачки колебаний «приведённая амплитуда модуляции ёмкости g».
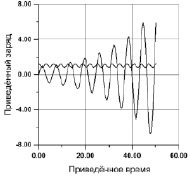
Рис. 4. Нарастающие колебания при токовой неустойчивости
Заключение
Следует отметить, что режим токовой неустойчивости колебательного контура не мог быть обнаружен в опытах Мандельштама – Папалекси [1]. Причина этого заключалась в том, что параллельно переменной ёмкости был установлен пробойник на 5 кВ, который защищал колебательный контур от срыва в токовую неустойчивость и переводил его работу в режим параметрических биений.
Эксперименты по обнаружению режима токовой неустойчивости требуют другого конструктивного решения для переменной воздушной ёмкости. Оно представлено на рис. 5. Возникающий в ней радиальный электрический пробой между П-образными пластинами статора 3 должен направлять основную часть энергии в колебательный контур, а не на нагрев воздуха, окружающего пластины конденсатора с разноимёнными зарядами.
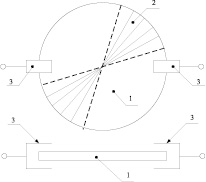
Рис. 5. Переменная ёмкость контура с токовой неустойчивостью: 1 – ротор-диск с набором радиальных проводящих секторов 2; 3 – П-образные пластины статора
Аналогичный конструктив ёмкости используется в швейцарской машине Поля Баумана (Paul Baumann, 1985) «Тестатика», вырабатывающей высоковольтную электрическую энергию [3–5]. То есть в основе работы машины «Тестатика» лежит механо-электрический принцип, открытый в 1950-х гг. Мандельштамом и Папалекси [1].
Отметим, что этот принцип известен миллионы лет жгутиковым бактериям, которые перемещаются в межклеточной жидкости. Опубликованные в январе 2018 г. в Nature работы биологов объяснили принцип их перемещения, названный flagellar motors [6]. Внутри осесимметричного тела бактерии, диаметром порядка 100 нм, располагаются несколько слоёв мембран. Каждая мембрана выполнена в виде пропеллера и содержит в себе проводящие радиальные сектора (как на рис. 5). Различные бактерии имеют от 13 до 17 радиальных секторов в роторе. Можно оценить среднее количество разделённых зарядов для пробойной напряженности электрического поля в жидкости 5 мВ/нм. Для всей мембраны оно составляет порядка 20 электронов. То есть на одном проводящем секторе мембраны размещается от одного до двух электронов. Такое разделение разноимённых зарядов и создает вращение бактерии, приводя её к перемещению в межклеточной жидкости.
Токовая неустойчивость колебательного контура, обнаруженная в заметке, представляет несомненный интерес для создания широкого класса электротехнических устройств, использующих механо-электрический принцип накопления зарядов. В перспективе они составят мощную альтернативу современным устройствам, работающим на законе электромагнитной индукции.
Выражаем благодарность В.А. Джанибекову за плодотворные обсуждения.
Библиографическая ссылка
Сапогин В.Г., Сапогин Л.Г., Сапогин К.В., Атаманченко А.К., Дзюба Д.А. ТОКОВАЯ НЕУСТОЙЧИВОСТЬ КОЛЕБАТЕЛЬНОГО КОНТУРА ПРИ ГАРМОНИЧЕСКОЙ МОДУЛЯЦИИ РЕАКТИВНОГО ПАРАМЕТРА // Международный журнал прикладных и фундаментальных исследований. – 2019. – № 4. – С. 44-48;URL: https://applied-research.ru/ru/article/view?id=12695 (дата обращения: 18.04.2024).