В самых различных отраслях промышленности в качестве рабочих и технологических агентов используют эмульсии несмешивающихся жидкостей. Значительные объемы рабочих жидкостей в виде масляных композиций, эмульсий, аэрозолей используют в технологических процессах машиностроения. В частности, их применяют для охлаждения рабочих поверхностей заготовок и инструмента при обработке металлов, смазки узлов станков и машин. Разработка новых и интенсификация существующих технологических процессов во многом связана с теплообменом при кипении жидкостных эмульсий [1, 2]. Поэтому исследование их гидродинамических и теплофизических характеристик в конкретных промышленных условиях остается одной из актуальных технических и научных задач [3, 4].
Нестационарный теплообмен при кипении жидкостных эмульсий весьма сложен не только для аналитического анализа, но и для экспериментального наблюдения [5–7]. Традиционный параметрический анализ сложных многофакторных процессов в эмульсиях несмешивающихся жидкостей с фазовыми превращениями зачастую носит формальный характер [8, 9]. Он не отражает того, что одни и те же размерные параметры могут одновременно входить в состав нескольких механизмов элементарных физических явлений (МЭФЯ) [10, 11]. Характер влияния переменных полностью предопределяется природой каждого из элементарных явлений, в которых они участвуют. Однако состав МЭФЯ формируется каждый раз частным образом в зависимости от параметров жидкостей и внешних условий. Поэтому каждая переменная может представлять результат совместного взаимосвязанного протекания различных по своей природе процессов, вклад каждого из которых неоднозначен.
Более определенным является выбор совокупности элементарных физических явлений, которые могут входить в состав сложного процесса при заданных внутренних и внешних условиях [12]. МЭФЯ обобщают разнородную теоретическую и эмпирическую информацию и обосновывают структуру критериальных зависимостей, которые обеспечивает сопоставимость моделей с реальными данными экспериментальных измерений.
Цель исследования: обоснование методики формирования моделей сложных, неформализуемых процессов теплообмена в жидкостных эмульсиях с фазовыми превращениями, использовании МЭФЯ в качестве инвариантных модельных элементов, уточнении структуры и состава феноменологических моделей, адекватных реальным технологическим условиям и априорным физическим представлениям.
Материалы и методы исследования
Механизмы элементарных физических явлений отражают существующие физические представления о тепловых процессах внутри перегретых капель жидкости в эмульсии. Известны два режима вскипания (нуклеации) однородной жидкости при температуре 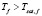 : у твердой поверхности нагрева (режим гетерогенной нуклеации) и в неограниченном объеме перегретой жидкости (режим гомогенной нуклеации). Эти же два вида нуклеации характерны для эмульсии с недогретой дисперсной фазой, когда, при температуре сплошной среды Tc,f, когда Tsat,d > Tc,f > Tsat,с, кипение сплошной среды эмульсии отличается от однородной жидкости наличием пузырьков пара наряду с каплями дисперсной фазы.
: у твердой поверхности нагрева (режим гетерогенной нуклеации) и в неограниченном объеме перегретой жидкости (режим гомогенной нуклеации). Эти же два вида нуклеации характерны для эмульсии с недогретой дисперсной фазой, когда, при температуре сплошной среды Tc,f, когда Tsat,d > Tc,f > Tsat,с, кипение сплошной среды эмульсии отличается от однородной жидкости наличием пузырьков пара наряду с каплями дисперсной фазы.
В эмульсии с недогретой сплошной средой с температурой Tc,f, когда Tc,f < Tsat,c, но с перегретой дисперсной фазой, при Tsat,c > Td,f > Tsat,d нуклеация происходит внутри капель. Прогрев всего объема капель до температуры Tsat,d насыщенных паров сдерживается парообразованием в перегретом шаровом слое у замкнутой межфазной поверхности, которая становится поверхностью нагрева с температурой Tc,f. Причем тепловая энергия, в отличие от кипения сплошной среды эмульсии, аккумулируется перегретым объемом капель.
Кипение в замкнутом объеме, ограниченном подвижной поверхностью
Парообразование в замкнутом объеме капель является принципиально новым видом кипения, который ограничен подвижной поверхностью нагрева. Он происходит в условиях, когда Tsat,c > Td,f > Tsat,d и может продолжаться до тех пор, пока капля полностью испарится и наступит равновесное состояние при температуре Td,v = Tc,f.
В эмульсии образование пузырьков пара с радиусом R происходит в каплях с диаметром d при давлении в сплошной среде Рс. В этих условиях внешнее давление получает приращение на величину двойного капиллярного давления
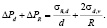 (1)
(1)
В связи с этим в каплях диспергированной жидкости внутри пузырьков пара температура насыщения Tsat,v повышается при изменении давления на величину 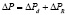 . По Клапейрону – Клаузиусу при фазовом переходе в однородной жидкости изменение давления вдоль кривой насыщения жидкости в жизнеспособном пузырьке пара с радиусом R* связано с изменением температуры следующим образом:
. По Клапейрону – Клаузиусу при фазовом переходе в однородной жидкости изменение давления вдоль кривой насыщения жидкости в жизнеспособном пузырьке пара с радиусом R* связано с изменением температуры следующим образом:
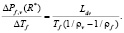 (2)
(2)
Перегрев 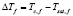 необходим для кипения однородной жидкости.
необходим для кипения однородной жидкости.
Для образования критических пузырьков пара в каплях перегретой жидкости с учетом капиллярного давления ΔPd необходим дополнительный перегрев 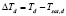 , который повышается с уменьшением размера капель. Полное аналитическое описание кипения в таких условиях в настоящее время не представляется возможным.
, который повышается с уменьшением размера капель. Полное аналитическое описание кипения в таких условиях в настоящее время не представляется возможным.
Качественные физические представления тепловых процессов внутри перегретых капель жидкости в эмульсии
Основное отличие кипения в каплях состоит в том, что фазовые превращения происходят в замкнутом пространстве, ограниченном эластичной, деформируемой поверхностью раздела в объеме сплошной среды. Парообразование не может изменить массы капли в условиях, если исключено ее дробление. Это пространство представляет собой закрытую термодинамическую систему, которая не рассеивает, а только аккумулирует тепловую энергию внешней сплошной среды. Но объем капли значительно увеличивается пропорционально различиям плотностей ее жидкого и парообразного состояния.
При кипении внутри капель проявляются следующие специфические особенности, которые учитываются при дальнейшем рассмотрении:
– тепловая энергия, которая поступает от сплошной среды, аккумулируется внутри объема дисперсной фазы;
– жизнеспособные пузырьки пара с радиусом R* образуются в приграничном слое перегретой жидкости на внутренней (вогнутой) поверхности капель;
– рост критических пузырьков пара R* внутри капель не может завершаться отрывом их от поверхности нагрева и способствовать сильной турбулизации в кипящей жидкости, характерной для кипения у твердой поверхности нагрева;
– изменение объема кипящих капель при переходе диспергированной жидкости в парообразное состояние сопровождается движением межфазной поверхности, которое может интенсифицировать конвективный теплообмен с окружающей сплошной средой;
– замкнутая межфазная поверхность нагрева обуславливает сохранение массы при кипении капель дисперсной фазы, но размеры их при этом могут изменяться.
С учетом этих физических представлений можно выделить структуры режимов кипения капель дисперсной фазы в жидкостных эмульсиях, определяют возможный состав МЭФЯ.
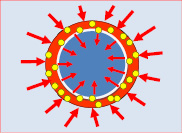
На рис. 1 представлены возможные составы МЭФЯ, соответствующие различным режимам кипения. Они аппроксимируют возможные состояния парожидкостных капель, которые соответствуют нестационарному процессу фазовых превращений, движущей силой которого является плотность теплового потока. Состояние термогидродинамического равновесия, подобного динамическому равновесию в изотермическом объеме эмульсии, наступить не может. Тепловой рост капель может продолжаться, в принципе, до полного перехода их в парообразное состояние. Но он может остановиться на некоторой стадии, если тепловой энергии окажется недостаточно для его продолжения.
|
|
Режим кипения I Притока теплоты достаточно для поддержания следующих элементарных физических явлений: – перегрева поверхности капли, – гетерогенной нуклеации на внутренней стороне сферической поверхности нагрева, – образования жизнеспособных зародышей паровой фазы, – незначительного увеличения объема капли с зародышами паровой фазы. |
|
|
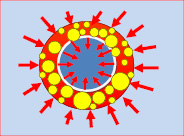
Режим кипения II Притока теплоты достаточно для поддержания следующих элементарных физических явлений процессов: – увеличения толщины внешнего перегретого слоя капли, – умеренного роста пузырьков пара критического размера, – прогрева внутреннего объема жидкого ядра капли. – заметного увеличения объема капли с пузырьками пара. |
|
|
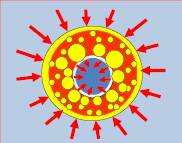
Режим кипения III Притока теплоты достаточно для поддержания следующих элементарных процессов: – формирования парового подслоя у внутренней поверхности капли, – перегрева парового подслоя – перегрева внешней поверхности жидкого ядра, – перехода растущих на ней пузырьков в паровой слой, – прогрева жидкого ядра, – значительного увеличения объема парожидкостной капли. |
Рис. 1. Режимы кипения перегретых капель дисперсной фазы в жидкостных эмульсиях
Результаты исследования и их обсуждение
Структура моделей переноса теплоты в замкнутой термодинамической системе
Тепловая энергия сплошной среды эмульсии с температурой Тс,0 расходуется на перегрев капель диспергированной жидкости, необходимый для парообразования. В дальнейшем рассмотрение ограничено режимом кипения III, представленным на рис. 1. В первом приближении полагается двухслойная схема теплообмена, перегрев будет обеспечиваться только шарового перегретого слоя, толщина которого фиксирована. Центральная часть объема капли сохраняет исходную температуру, поскольку теплота после прогрева подслоя до Tsat,d будет затрачена на превращение его пар.
Распределение теплового потока q от сплошной среды через межфазную поверхность ∑Sd к кипящей внутри нее однородной диспергированной жидкости представлено в таблице следующим образом:
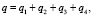 (3)
(3)
где q1 – поток теплоты через перегретый подслой у межфазной поверхности за счет теплопроводности, q2 – затраты теплоты на прогрев объема капли, q3 – затраты на испарение части капли и q4 – теплота перегретого пара.
Тепловой баланс эмульсии при фазовом превращении перегретых капель
|
|
|
+ |
+ |
|
1 |
2 |
3 |
4 |
|
Теплота – источник сплошная среда – поступает в капли через суммарную поверхность |
Затраты теплоты на прогрев в каплях шарового слоя пара толщиной δv |
Подвод теплоты через паровой слой ко всей поверхности |
Испарение массы Δmd,f перегретого слоя на поверхности жидкого ядра всех капель с радиусом Rd,f |
Составляющая q1 у межфазной поверхности нагрева существенно отличается от аналогичной составляющей при кипении жидкости у твердой стенки:
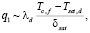 (4)
(4)
где Тc,f , Тsat,d – температуры поверхности капли и её насыщенных паров, λd – коэффициент теплопроводности диспергированной жидкости. Толщина перегретого шарового слоя пара 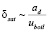 в замкнутом объеме, изменение которой обусловливает движение межфазной поверхности, характеризуемое скоростью кипения uboil, аd – коэффициент температуропроводности диспергированной жидкости.
в замкнутом объеме, изменение которой обусловливает движение межфазной поверхности, характеризуемое скоростью кипения uboil, аd – коэффициент температуропроводности диспергированной жидкости.
Вторая составляющая q2 представляет затраты этой теплоты на прогрев капли до температуры насыщенных паров Тsat,d. Третья составляющая q3 представляет затраты теплоты на испарение жидкости в перегретом подслое. Четвертая составляющая q4 характеризует сохранение теплоты в форме энтальпии паровой фазы.
Упрощенная схема теплового баланса необходима лишь для качественного анализа этого физического явления и обоснования системы безразмерных критериев подобия, представляющих возможные механизмы переноса теплоты. Она достаточно хорошо соответствует теплофизическим данным, представленным на рис. 2, которые получены в результате экспериментальных наблюдений [13].
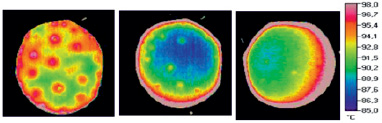
Рис. 2. Термограммы пузырькового кипения капель водного раствора LiBr (Misyura, 2018)
Полагая, что начальная стадия парообразования в капле, связанная с формированием шарового слоя, завершена, продолжение этого процесса требует прогрева образовавшегося пара толщиной δv и переноса теплоты к недогретому жидкому ядру с радиусом RR,f. Для прогрева шарового слоя пара необходимо количество теплоты, затраченное на испарение, 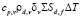 .
.
Испарение поверхностного слоя δsat жидкого ядра капли требует количества теплоты 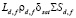 , которое необходимо для прогрева его до температуры насыщенных паров. Толщина этого слоя определяется дополнительными затратами на парообразование:
, которое необходимо для прогрева его до температуры насыщенных паров. Толщина этого слоя определяется дополнительными затратами на парообразование:
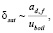 (5)
(5)
аd,f – коэффициент температуропроводности диспергированной жидкости.
Парообразование происходит у межфазной поверхности, что сдерживает дальнейший прогрев внутреннего объема капли до тех пор, пока не испарится определенная часть этого слоя. Одной из характеристик интенсивности этого физического явления может служить скорость кипения uboil:
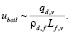 (6)
(6)
Она определяется переносом теплоты теплопроводностью перегретого пара
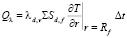 , (7)
, (7)
ограниченного пространством шарового слоя под межфазной поверхностью капли. Поэтому трансформация диспергированной жидкости в пар сопровождается увеличением только ее объема и межфазной площади при сохранении исходной массы. Замкнутость парожидкостной системы обусловливает также непосредственную взаимосвязь МЭФЯ переноса теплоты, которая в открытой системе носит принципиально иной характер [14, 15].
В перегретом слое подвод теплоты Qλ обеспечивает испарение перегретого слоя на поверхности жидкого ядра капли с радиусом Rd,f массой 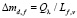 . В замкнутом объеме парожидкостной капли объем пара той же массы
. В замкнутом объеме парожидкостной капли объем пара той же массы 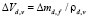 . Связь между толщиной слоя испарившейся диспергированной жидкости
. Связь между толщиной слоя испарившейся диспергированной жидкости 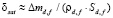 и слоя образовавшегося пара
и слоя образовавшегося пара 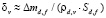 принимает следующий вид:
принимает следующий вид:
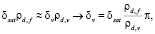 (8)
(8)
где 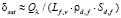 .
.
Пример модельной структуры теплообмена, представленный в таблице, дает общее представление о предполагаемом составе МЭФЯ сложного процесса теплообмена при кипении диспергированной жидкости внутри объема, ограниченном межфазной поверхностью капель. В состав этих явлений, количество которых зависит от режима кипения, может входить большое число физических параметров, что затрудняет формулировку замкнутой аналитической модели. В некоторые составляющие входят одни и те же параметры, что обусловливает взаимодействие элементов структуры. Для описания их необходимы дополнительно замыкающие соотношения, которые обычно носят эмпирический характер. Однако такую структуру можно использовать для обоснования состава безразмерных критериев, которые соответствуют совокупности МЭФЯ переноса теплоты, участвующих в формировании сложного физического процесса теплообмена.
Представление механизмов элементарных явлений переноса теплоты в форме безразмерных критериев
Механизмы переноса теплоты в физической модели теплового баланса при кипении капель дисперсной фазы эмульсии нужно представить в форме безразмерных критериев, которые будут входить в состав модельной зависимости. Они получаются из отношения составляющих 1–4 энергетического баланса таблицы, которые отражают влияние предполагаемых механизмов элементарных процессов переноса теплоты в рамках конкретного режима кипения. Так, отношение составляющих 1 и 3 приводит к следующей форме критерия Нуссельта:
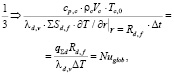 (9)
(9)
где 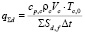 – суммарный тепловой поток от сплошной среды эмульсии к диспергированной жидкости, которая охлаждается из-за испарения жидкого ядра капель. Концентрация дисперсной фазы представлена здесь суммарной площадью поверхности капель с радиусом Rd,f в единице объема сплошной среды
– суммарный тепловой поток от сплошной среды эмульсии к диспергированной жидкости, которая охлаждается из-за испарения жидкого ядра капель. Концентрация дисперсной фазы представлена здесь суммарной площадью поверхности капель с радиусом Rd,f в единице объема сплошной среды 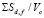 . В качестве продолжительности Δt нужно использовать аналогичную характеристику физического явления, которым определяется интенсивность испарения.
. В качестве продолжительности Δt нужно использовать аналогичную характеристику физического явления, которым определяется интенсивность испарения.
Отношение составляющих 1 и 3 приводит к «тепловой» форме критерия Рейнольдса:
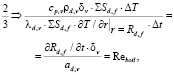 (10)
(10)
где 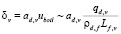 ,
, 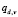 – затраты теплоты, необходимой для испарения жидкости в шаровой слой в капле дисперсной фазы, определены средней массовой скоростью отвода паровой фазы
– затраты теплоты, необходимой для испарения жидкости в шаровой слой в капле дисперсной фазы, определены средней массовой скоростью отвода паровой фазы 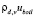 от ее поверхности. Скорость роста капель
от ее поверхности. Скорость роста капель 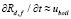 соответствует скорости движения межфазной поверхности.
соответствует скорости движения межфазной поверхности.
Критерий Ja формируется из соотношений составляющих теплового баланса 2 и 4:
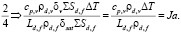 (11)
(11)
Полученные критерии представляют совокупность механизмов элементарных явлений, формирующих рассматриваемый режим кипения III. Вначале его представляют наиболее простым регрессионным соотношением, связывающим два самых существенных критерия, связанных с преобладанием механизмов теплообмена без заметного влияния процесса парообразования:
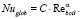 (12)
(12)
Если их окажется недостаточно, то разброс экспериментальных данных относительно модельной кривой окажется значительным. В этом случае корреляционное соотношение необходимо расширить еще одним элементарным явлением. Критерий Ja отражает затраты теплоты на обеспечение нуклеации на внутренней стороне сферической поверхности нагрева и образования жизнеспособных зародышей паровой фазы
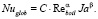 (13)
(13)
Характер и форма предполагаемой нелинейной критериальной взаимосвязи оцениваются на основе данных экспериментального исследования процесса теплообмена в реальных условиях. Правильность модельного представления сложного физического явления обосновывается статистической значимостью выбранного регрессионного соотношения, в данном случае (12)–(13). Адекватность экспериментальным данным такой взаимосвязи является подтверждением соответствия структуры модели реальному составу элементарных физических явлений. При этом результаты методов обычного формального корреляционно-регрессионного анализа приобретают наглядное физическое содержание, а результаты экспериментальных исследований получают адекватную интерпретацию.
Заключение
В настоящее время тепловые процессы в жидкостных эмульсиях с фазовыми переходами изучены недостаточно глубоко, что затрудняет проектирование и эксплуатацию промышленного оборудования. Необходимо более детальное представление особенностей кипения, связанное с неоднозначным поведением фаз эмульсии в парожидкостном состоянии. Разнообразным по составу элементарных физических явлений режимам кипения в неоднородной среде эмульсии соответствуют характеристики теплообмена, связанные с влиянием большого числа факторов. Структурное представление поведения кипящих эмульсий способствует правильному выбору частных моделей сложных физических процессов, которые невозможно полностью описать общими теоретическими уравнениями.
Модель структуры сложного процесса теплообмена предлагает выбор состава элементарных физических явлений, которые постулируются на основании априорной теоретической и эмпирической информации. Каждому гипотетическому составу элементарных явлений ставится в соответствие предполагаемый состав безразмерных критериев в регрессионной модели. Их физическое содержание обеспечивает предметную интерпретацию экспериментальных данных, адекватную характеру реального физического процесса тепло- и массообмена. С другой стороны, оценки констант эмпирической регрессионной зависимости, их адекватность и статистическая значимость параметров регрессии служат обоснованием приемлемости принятых модельных представлений.
Библиографическая ссылка
Розенцвайг А.К., Страшинский Ч.С. СТРУКТУРНЫЙ ПОДХОД К МОДЕЛИРОВАНИЮ СЛОЖНЫХ ПРОЦЕССОВ ТЕПЛООБМЕНА ПРИ КИПЕНИИ ЖИДКОСТНЫХ ЭМУЛЬСИЙ // Международный журнал прикладных и фундаментальных исследований. 2019. № 4. С. 60-66;URL: https://applied-research.ru/ru/article/view?id=12698 (дата обращения: 13.03.2026).
DOI: https://doi.org/10.17513/mjpfi.12698


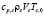 =
=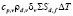 +
+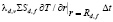
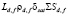
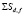
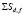 жидкого ядра капель
жидкого ядра капель