Автором термина «вейвлет» (wavelet) являются Гроссманн (Grossmann) и Морле (Morlet). Они в середине 1980-х гг. при анализе свойств сейсмических и акустических сигналов ввели этот термин [1]. Их работа послужила толчком исследования вейвлетов рядом ученых, таких как Добеши, Мейер, Малл, Фарж, Чуи и др. Термин «вейвлет» звучит как маленькая или короткая волна. Малость относится к условию, что эта функция имеет конечную длину (компактный носитель). Волна относится к условию, что функция колебательная (осциллирующая). В некоторых русскоязычных литературах термин «вейвлет» переведен как «всплеск». Далее мы используем этот термин. К всплеску можно применить две операции: сдвиг и масштабирование. Под сдвигом понимается перемещение области его локализации во времени; а под масштабированием растяжение или сжатие, т.е. перемещение области его локализации по частоте. Использование операций сдвиг и масштабирование, с учетом свойства локальности всплеска в частотно-временной области, позволяет нам анализировать данные на различных масштабах и точно определять положение их характерных особенностей во времени [2, 3]. В работе [4] исследованы реализации сплайн-всплескового разложения первого порядка. А в [5] интерполяционные всплески применены в краевых задачах Дирихле в круге для однородного уравнения с оператором Лапласа.
В [6] было доказано, что полуортогональные кубические мультивсплески на суперкомпактном носителе, равном носителю базисного сплайна, можно построить относительно скалярного произведения с производными. В [3] для случая сплайнов третьей степени получен алгоритм всплеск-преобразования в виде решения трехдиагональной системы линейных уравнений со строгим диагональным преобладанием. Представлены результаты численных экспериментов по вычислению производных дискретно заданной функции. Применение эрмитовых мультивсплесков седьмой степени для решения дифференциальных уравнений четвертого порядка рассмотрено в [7].
Цель исследования: применить Эрмитовы кубические сплайн-всплески к численному решению обыкновенных дифференциальных уравнений и показать преимущества предлагаемого метода.
Результаты исследования и их обсуждение
Введем следующие обозначения:
H1(0,1) – пространство непрерывных функций на интервале (0,1), т.е. 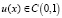 таких, что
таких, что 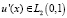 ;
;
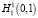 – замыкание множества
– замыкание множества 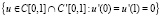 в H1(0,1);
в H1(0,1);
П3 – множество кубических многочленов;
Vn – пространство кубических сплайнов, удовлетворяющих следующим условиям, n > 0:
а) 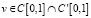 ;
;
б) 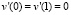 ;
;
в) 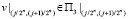 ,
,
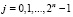 j = 0,…,2n –1;
j = 0,…,2n –1;
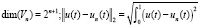 ,
,
C(An) – число обусловленности матрицы An.
Ранее построенные всплески, например вейвлеты Добеши, Мейер, Малл, Фарж, Чуи и др., не имеют аналитического представления и расположены на достаточно широком носителе. Эти свойства можно считать недостатками всплесков. Аналитическое представление всплесков с суперкомпактным носителем удачно подходит к применению всплесков для численного анализа. В работах [6] предложен новый подход к построению базисных всплесков с суперкомпактным носителем на пространстве эрмитовых кубических сплайнов, т.е. всплески ортогональны со скалярным произведением производных 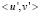 . Всплески ортогональные со скалярным произведением производных
. Всплески ортогональные со скалярным произведением производных 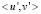 лучше подходят для применения мультивсплесков к численному решению дифференциальных уравнений второго порядка. В работах [8, 9] эти всплески применены для решения интегро-дифференциальных уравнений второго порядка.
лучше подходят для применения мультивсплесков к численному решению дифференциальных уравнений второго порядка. В работах [8, 9] эти всплески применены для решения интегро-дифференциальных уравнений второго порядка.
Пусть f1 и f2 кубические сплайны вида [8, 9]:
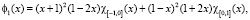
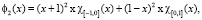
где 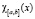 – характеристическая функция,
– характеристическая функция, 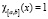 , при
, при 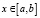 и
и 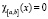 , при
, при 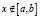 .
.
Множество 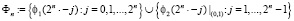 , является базисом для пространства Vn. Элементы множества Фn обозначим через
, является базисом для пространства Vn. Элементы множества Фn обозначим через 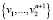 .
.
Множество всплесков обозначим через Ψn:
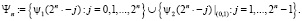
Пространство, натянутое на множество всплесков, обозначим через Wn. Нетрудно заметить, что размерность этого пространства 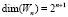 .
.
Всплески Ψ1, Ψ2 конкретизируются ниже.
В работе [6] доказано следующее равенство:
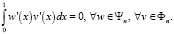 (1)
(1)
Пересечение пространств сплайнов Vn и всплесков Wn не пустое, т.е. 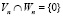 . Как отмечено выше, размерности этих пространств
. Как отмечено выше, размерности этих пространств 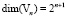 ,
, 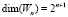 и если учитывать, что cумма
и если учитывать, что cумма 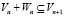 то
то
dim(Vn + Wn) = dim(Vn) + dim(Wn) = 2n + 1 + 2n + 1 = 2n + 2 = dim(Vn + 1).
Отсюда получаем, что Vn + 1 = Vn⊕Wn, т.е. V n + 1 = Vn⊕Wn, Vn = Vn–1⊕Wn–1, ..., V3 = V2⊕W2, V2 = V1⊕W1. Таким образом, получаем разложение пространства 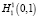 :
:
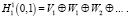
Как отмечено выше, F1 = {v1, v2, v3, v4}; а элементы множества вейвлетов Yn обозначим через Yn = {w2 n + 1,…, w2 n + 2}, n∈N.
Теперь приступим к построению базиса Рисса.
Введем обозначение, пусть gk: = vk/||v'k||2 при k = 1,2,3,4 и gk: = wk/||w'k||2 при k > 4. Тогда ||g'k||2 = 1 при n∈N. Последовательность (g'k)k∈N является последовательностью Рисса в L2(0,1) [8, 9].
Очевидно, что эрмитовы кубические сплайны f1 и f2 удовлетворяют условиям
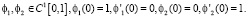
Поэтому эрмитова интерполяция для непрерывно дифференцируемой функции в оси 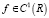 имеет следующий вид:
имеет следующий вид:
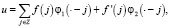
где 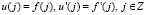 .
.
Пусть пространство S представляет собой инвариантное пространство сдвигов, порожденное сплайнами f1 и f2. В таком случае, функция g принадлежит пространству S тогда и только тогда, когда существуют две последовательности b1, b2 на множестве целых чисел Z, для которых выполняется равенство [8, 9]:
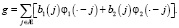
Пусть S1 = {g(2•): g∈S}, тогда S⊂S1. Мы ищем пространство всплесков W, для которого выполняется условие S1 = S⊕W, т.е. «дополняет» пространство S до S1. Мы ищем два всплеска ψ1, ψ2, сдвиги которых порождают пространство всплесков W. Учитывая (1), также требуем выполнение равенств
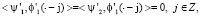
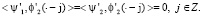 (2)
(2)
Для этой цели нам необходимо вычислить скалярное произведение производных сдвигов кубических эрмитовых сплайнов f1 и f2. Заметим, что
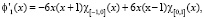
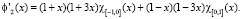
Предположим, что искомые всплески имеют вид
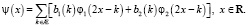
Вычисляя скалярное произведение с производными, получим
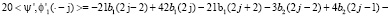
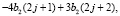
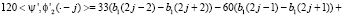
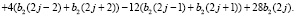
Чтобы найти неизвестные коэффициенты, введем преобразование Лапласа последовательностей b1, b2 на множестве целых чисел. Здесь положительная или отрицательная степень z означает сдвиг на один шаг по шаблону узлов эрмитового сплайна вправо или влево. Тогда
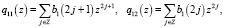
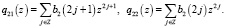
Составляем функциональное уравнение. Решение функционального уравнения
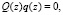
где z∈C\{0}, j∈Z, 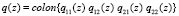 ,
,
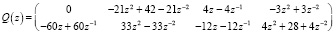 ,
,
будет означать, что скалярное произведение с производными равняется нулю, т.е.
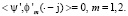
Решая функциональное уравнение, находим два линейно независимых решения:
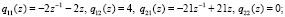
и
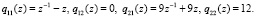
Эти два решения порождают искомые всплески y1, y2, их также называют материнскими всплесками:
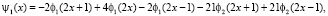
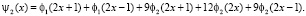
Носителями построенных всплесков ψ1, ψ2 является отрезок от –1 до 1, они удовлетворяют условию (2), и их сдвиги генерируют пространство всплесков W, так что S1 является прямой суммой S и W. Кроме того, y1 – симметричен, а y2 – антисимметричен.
Теперь мы построим всплеск-базис в пространстве 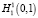 из этих сплайн-всплесков. Пусть выполняется равенство (1) и
из этих сплайн-всплесков. Пусть выполняется равенство (1) и 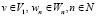 , тогда имеем, что для любого натурального n выполняется соотношение
, тогда имеем, что для любого натурального n выполняется соотношение
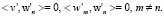
Отсюда, получаем равенство
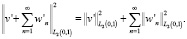
Пусть, при 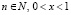 :
:
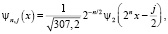 при
при 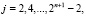
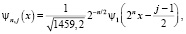 при
при 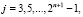
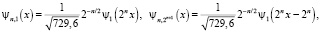
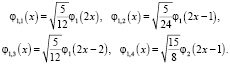
Тогда имеем
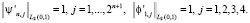
Ясно, что пространство V1 разлагается на 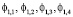 . Отсюда следует, что
. Отсюда следует, что 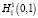 разлагается на
разлагается на 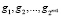 , здесь
, здесь 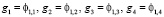 ,
, 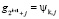 , k = 1, 2,..., n–1, j = 1,…,2n.
, k = 1, 2,..., n–1, j = 1,…,2n.
Нетрудно доказать, что 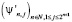 является базисом Рисса в L2(0,1), или можно посмотреть [6].
является базисом Рисса в L2(0,1), или можно посмотреть [6].
Применение. В этом разделе мы используем построенные всплески для решения дифференциальных уравнений второго порядка вида
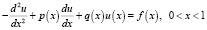 , (3)
, (3)
с граничным условием Неймана
u'(0) = u'(1) = 0, (4)
где 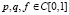 . Коэффициенты уравнения (4) удовлетворяют условиям: 0 ≤ p(x) ≤ c3, 0 ≤ q(x) ≤ c4, x∈[0,1].
. Коэффициенты уравнения (4) удовлетворяют условиям: 0 ≤ p(x) ≤ c3, 0 ≤ q(x) ≤ c4, x∈[0,1].
Если q(x)≡0, то для разрешимости задачи (3)–(4) требуем выполнение условия
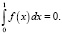
Введем билинейную форму a(u, v):
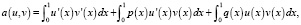
где 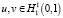 .
.
Учитывая билинейную форму, задачу (3)–(4) можно записать в виде
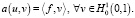
Отсюда получаем задачу Галеркина:
Найти 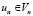 , для которых выполняется равенство
, для которых выполняется равенство
a(un, v) = <f, v> ∀v∈Vn. (5)
Задача (5) имеет единственное решение [10]. Мы будем использовать выше построенное множество всплесков G = {g1,…,g2n + 1} как базис для пространства Vn. Тогда задача (5) дискретизируется следующим образом:
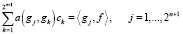 .
.
Введем обозначение 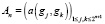 .
.
Экспериментальная часть. Ниже привели применение построенных базисных всплесков Gn к конкретным дифференциальным уравнениям.
Вычисления проведены в системе MathCad 15.
Пример 1. –u'' + u = 2t3–3t2–12t + 6, u'(0) = u'(1) = 0.
Точное решение u(t) = 2t3–3t2,
численное решение u16(t) = –5,821×10–6 g1(t)–1,095g2(t)–1,549g3(t)–0,548g4(t)–
–1,736×10-7 g5(t)–2,021×10–11 g6(t) + 1,742×10–7 g7(t) + 6,122×10–7 g8(t) +
+ 2,205×10–6 g9(t) + 3,702×10–7g10(t) + 1,044×10–6 g11(t) + 9,274×10–7g12(t) +
+ 5,646×10–7g13(t)–1,312×10–6 g14(t) + 3,148×10–6 g15(t) + 4,187×10–7g16(t);
||u(t)–u4(t)||2 = 3,933×10–6, ||u(t)–u8(t)||2 = 3,933×10–6, ||u(t)–u16(t)||2 = 3,933×10–6,
С(A4) = 19,69; С(A8) = 19,69, С(A16) = 19,69.
Пример 2. –u'' + etu = p2cos(pt) + etcos(pt), u'(0) = u'(1) = 0.
Точное решение u(t) = cos(pt),
численное решение u8(t) = 1,556g1(t)–2,771×10-6 g2(t)–1,556g3(t)–1,179g4(t)–
–0,026g5(t) + 5,798×10–7g6(t) + 0,026g7(t) + 0,029g8(t);
||u(t)–u4(t)||2 = 2,389×10–3, ||u(t)–u8(t)||2 = 2,092×10–4, ||u(t)–u16(t)||2 = 1,468×10–5,
С(A4) = 1,723; С(A8) = 2,342, С(A16) = 3,201.
Пример 3. –u'' + u' + u = t4 + 2t3–17t2 + 14t–2, u'(0) = u'(1) = 0.
Точное решение u(t) = t2(1–t)2,
численное решение: u8(t) = 3,502×10-3 g1(t) + 0,142g2(t) + 3,331×10-3 g3(t)–1,503×10-5 g4(t)–
–0,019g5(t)–0,026g6(t)–0,019g7(t) + 5,576×10-5 g8(t);
||u(t)–u4(t)||2 = 1,37×10–3, ||u(t)–u8(t)||2 = 1,528×10–4, С(A4) = 20,9; С(A8) = 21,21.
Следует отметить, что численные результаты показывают, что точность улучшается с повышением n. И значение n не влияет на число обусловленности матрицы An.
Работа выполнена при поддержке МОиН КР.
Библиографическая ссылка
Кудуев А.Ж., Турсунов Э.А., Абдыкалык Ж.А., Турсунов Д.А. ПРИМЕНЕНИЕ МУЛЬТВЕЙВЛЕТОВ К ЧИСЛЕННОМУ РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА // Международный журнал прикладных и фундаментальных исследований. 2019. № 6. С. 153-158;URL: https://applied-research.ru/ru/article/view?id=12785 (дата обращения: 27.12.2025).
DOI: https://doi.org/10.17513/mjpfi.12785

