Идея квантового моделирования возникла в начале 1980-х гг. в результате реализации фундаментальной сложности эмуляции сложной квантовой системы с использованием классических компьютеров. Со временем эта идея превратилась в основу квантовых вычислений. Подобно квантовым компьютерам, квантовые симуляторы основаны на сетях квантовых битов (кубитов), но, в отличие от полноценных квантовых компьютеров, квантовые симуляторы не используют операции с дискретными затворами и коды исправления ошибок. Квантовые симуляторы с настраиваемыми параметрами предназначены для эмуляции только определенных типов гамильтонианов.
Тем не менее можно показать, что очень общий гамильтониан можно моделировать, по-видимому, ограниченным классом спиновых цепей с взаимодействиями XX и YY. В скором будущем такие тренажеры будут способствовать разработке новых квантовых систем и изучению явлений и режимов, недоступных в прошлом. Кроме того, квантовые симуляторы дают возможность экспериментального изучения квантового отжига в контексте адиабатических квантовых вычислений.
Наше исследование основано на перестраиваемых одномерных массивax Джозефсона с контролируемыми взаимодействиями, которые имитируют квантовые одномерные модели. Интегрируемая модель одномерной спиновой цепи Изинга в поперечном магнитном поле служит парадигмой в контексте неравновесной термодинамики и квантово-критических явлений. Как модели Изинга в поперечном поле, так и модели XY, относящиеся к широкому кругу физических систем, сыграли решающую роль в понимании квантовых фазовых переходов. За последние пятьдесят лет эти модели породили огромную теоретическую активность. В последнее время эти модели сыграли решающую роль в разработке методов квантового отжига и адиабатических квантовых алгоритмов. Адиабатические квантовые вычисления представляют собой один из подходов к построению квантовых вычислений, основанный на адиабатической теореме, близкий к квантовому отжигу. Идея метода заключается в рассмотрении гамильтониана сложной задачи, как гамильтониан некоторой более простой задачи и некоторая добавка, которая в процессе эволюции квантовой системы приводит к гамильтониану исходной задачи. Интерес представляет основное состояние системы. Адиабатическая теорема гарантирует, что при достаточно медленной эволюции система будет оставаться в основном состоянии. Было доказано, что адиабатические квантовые вычисления эквивалентны «стандартным» или квантовым вычислениям модели ворот. Однако адиабатические вычисления достаточно перспективны для задач оптимизации, целью которых является минимизация (или максимизация) функции, каким-то образом связанной с этой проблемой, то есть поиск экземпляра, который минимизирует (или максимизирует) эту функцию [1].
В прошлом экспериментальное исследование квантовой спиновой динамики в 1D было в значительной степени ограничено микроскопическими спинами в системах с конденсированным веществом. Было продемонстрировано, что такие квазиодномерные спиновые материалы, как LiH0F4 и C0Nb2O6, могут непрерывно перестраиваться через квантовый фазовый переход (КФП). Хотя эти работы открыли новые перспективы в исследованиях модели Изинга в поперечном поле, экспериментальная реализация одномерных моделей квантовых спинов в хорошо управляемых и перестраиваемых системах остается сложной задачей.
В качестве экспериментального инструмента квазиодномерные спиновые системы в твердых телах ограничены в нескольких отношениях:
1) межцепные взаимодействия не являются пренебрежимо слабыми, и, следовательно, эти системы неизбежно являются квазиодномерными;
2) обменные взаимодействия между спинами ближайшего соседа не могут быть изменены;
3) обменные взаимодействия одинаковы для всех пар спинов, что не позволяет исследовать влияние беспорядка и межфазных границ без добавления значительного количества примесей;
4) доступный экспериментальный инструмент для этих систем – рассеяние нейтронов – взаимодействует только с узким классом возбуждений.
Гибкость в проектировании искусственных спиновых систем, свободных от этих ограничений, способствует преодолению разрыва между теоретическим исследованием идеальных спиновых цепей и экспериментальным исследованием объёмных магнитных образцов. В частности, эта гибкость позволяет решать важную проблему влияния беспорядка на статику и динамику спиновых моделей поперечного поля. Недавно модель Изинга в поперечном поле была реализована в цепочке искусственных и полностью управляемых спинов – восьми кубитов потока с перестраиваемыми спин-спиновыми связями. Мы придерживаемся аналогичного подхода, используя специально разработанные одномерные лестницы Джозефсона [2].
Мы предлагаем новую платформу для исследования квантовых фазовых переходов в одном измерении. В этой работе мы собираемся описать работу системы, состоящей из специально разработанной цепочки асимметричных СКВИДов. Разрабатываем теоретическое описание низкоэнергетической части спектра. В частности, мы показываем, что система обладает квантовым фазовым переходом типа Изинга. В микроволновых экспериментах с этой системой мы исследовали фазовые границы между упорядоченной и неупорядоченной фазами и критическое поведение низкоэнергетических мод системы вблизи перехода.
Лестницы Джозефсона
Лестницы Джозефсона, предназначенные для исследования одномерных (1D) КФП, представляют собой 1D цепочку связанных асимметричных сквидов (рис. 1). Элементарная ячейка лестниц похожа на ячейку Джозефсона, разработанную как супериндукторы (элементы с СВЧ-сопротивлением, значительно превышающим квант сопротивления h/e2). Каждая элементарная ячейка содержит один меньший переход с энергией Джозефсона EJS в одном плече и три больших перехода Джозефсона с энергией Джозефсона EJL в другом плече. Соседние ячейки соединены между собой через одно большее соединение.
Лестницы характеризуются соотношением энергий Джозефсона больших и меньших переходов, r ≡ Eл./EJS. Для r, больших критического значения r0, энергия лестницы Джозефсона, как функция фазы φ поперек лестницы, имеет только один минимум r > r0 при φ = 0 независимо от величины внешнего магнитного поля, перпендикулярного плоскости лестницы. Значение r0 зависит от длины лестницы и от силы квантовых флуктуаций (в квазиклассическом случае r0 = 5 для бесконечно длинной лестницы). Режим, где лестница может быть охарактеризована Джозефсоном как индуктивность, описываемая выражением
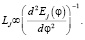
Если r > r0, зависимость двойных минимумов EJ(φ) реализуется в диапазоне магнитного потока 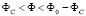 , где ФC является критическим
, где ФC является критическим 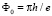 , это квант потока (рис. 1, в).
, это квант потока (рис. 1, в).
На рис. 1 панель (а) показывает, что единичные ячейки лестницы включают в себя все меньшие и большие Джозефсоновские переходы с энергиями Джозефсона EJS и EJL соответственно. Все ячейки имеют одинаковый магнитный поток; разность фаз по лестнице составляет φ2 – φ1 = φ. На панели (б) продемонстрирована конструкция лестницы. Нижние электроды туннельных переходов Джозефсона показаны синим цветом, верхние электроды – красным. Панель (в): энергия Джозефсона EJ(φ) лестницы с соотношением 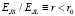 рассчитывается для трех значений потока: Φ = 0 (пунктирная кривая), Φ = ΦC (сплошная кривая) и
рассчитывается для трех значений потока: Φ = 0 (пунктирная кривая), Φ = ΦC (сплошная кривая) и 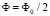 (пунктирная кривая). Энергия является периодической по фазе с периодом 2π, здесь показана только одна ветвь. На панели (г) показана фазовая диаграмма лестниц на r – плоскости. Для
(пунктирная кривая). Энергия является периодической по фазе с периодом 2π, здесь показана только одна ветвь. На панели (г) показана фазовая диаграмма лестниц на r – плоскости. Для 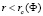 фаза нарушенной симметрии образуется при
фаза нарушенной симметрии образуется при 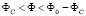 в результате фазового перехода типа Изинга. Граница этой области упорядоченного состояния показана в виде сплошной черной кривой. Расширение флуктуационного режима имеет порядок δr ≈ 0,1 для реалистичных массивов. Разрушение метрики происходит при критическом значении потока ΦC(r), и энергия минимума EJ(φ) превращается в функцию двойного минимума. Индуктивность Джозефсона расходится с приближением ΦC(r) (отсюда и термин супериндуктивность); квантовые флуктуации фазы устраняют расхождение.
в результате фазового перехода типа Изинга. Граница этой области упорядоченного состояния показана в виде сплошной черной кривой. Расширение флуктуационного режима имеет порядок δr ≈ 0,1 для реалистичных массивов. Разрушение метрики происходит при критическом значении потока ΦC(r), и энергия минимума EJ(φ) превращается в функцию двойного минимума. Индуктивность Джозефсона расходится с приближением ΦC(r) (отсюда и термин супериндуктивность); квантовые флуктуации фазы устраняют расхождение.
В режиме двойных минимумов направление токов в элементарных ячейках лестницы, индуцированных внешним магнитным полем, можно рассматривать как два состояния псевдоспинов 1/2. По мере увеличения потенциального барьера между этими состояниями, флуктуации квантовой фазы уменьшаются и возникает состояние глобальной нарушенной симметрии. Появление потенциала двойной ямы в одной ячейке не означает глобального фазового перехода во всей системе. Крупномасштабные квантовые флуктуации разрушают глобальный параметр порядка, если барьер между двумя минимумами слишком мал.
Параметр глобального порядка формируется при 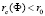 в результате фазового перехода типа Изинга (
в результате фазового перехода типа Изинга (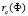 соответствует сплошной черной кривой на рис. 1, г). Расширение флуктуационного режима имеет порядок δr ≈ 0,1 для реалистичных массивов. Нужно отметить, что магнитное поле, которое ведет лестницу через квантовый фазовый переход, соответствует неравенству
соответствует сплошной черной кривой на рис. 1, г). Расширение флуктуационного режима имеет порядок δr ≈ 0,1 для реалистичных массивов. Нужно отметить, что магнитное поле, которое ведет лестницу через квантовый фазовый переход, соответствует неравенству 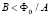 , где А представляет собой площадь элементарной ячейки, очень слабо [3].
, где А представляет собой площадь элементарной ячейки, очень слабо [3].
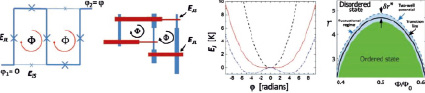
а) б) в) г)
Рис. 1. Элементарные ячейки, потенциальная энергия и фазовая диаграмма Джозефсоновской лестницы
Подчеркнем, что Джозефсоновские лестницы с 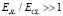 имеют экспоненциально малую вероятность процессов проскальзывания фазы, в которых фаза поперек лестницы изменяется на ∼2π. Это означает, что заряды статического смещения на отдельных островках не влияют на квантовые состояния лестницы. Влиянием этих зарядов и процессов проскальзывания фазы можно пренебречь. Оценку скорости проскальзывания фазы можно найти в [4].
имеют экспоненциально малую вероятность процессов проскальзывания фазы, в которых фаза поперек лестницы изменяется на ∼2π. Это означает, что заряды статического смещения на отдельных островках не влияют на квантовые состояния лестницы. Влиянием этих зарядов и процессов проскальзывания фазы можно пренебречь. Оценку скорости проскальзывания фазы можно найти в [4].
Физика низких энергий лестниц, близких к КФП, может быть отображена на модели φ4, которая имеет отношение к широкому кругу физических явлений, от ограничения кварков до ферромагнетизма. Вблизи критической точки эта модель эквивалентна интегрируемой модели одномерной спиновой цепочки Изинга [5] в поперечном магнитном поле.
Гибкость конструкции массива и настраиваемость параметров отдельных Джозефсоновских переходов предлагают несколько уникальных возможностей для исследования одномерных квантовых фазовых переходов. Например, эта новая платформа облегчает изучение влияния неинтегрируемости и беспорядка на КФП и появления эргодического поведения в почти интегрируемых квантовых системах.
Экспериментальные данные. Микроволновые измерения были разработаны для изучения спектра низкоэнергетических мод Джозефсоновских лестниц вблизи 1D КФП и «времени жизни» этих мод.
Экспериментальная установка для этих спектральных измерений и измерений во временной области была описана в [6]. В этих экспериментах Джозефсоновская лестница соединялась с резонатором считывания с сосредоточенными элементами через кинетическую индуктивность LC узкой сверхпроводящей пленки. Лестницы, схемы считывания и линия передачи микроволн (MW) на чипе были изготовлены с использованием многоуглового электронно-лучевого осаждения Al-плёнок через отрывную маску [7].
Размеры Джозефсоновских контактов в плоскости варьировались между 0,1×0,1 µм2 и 0,3×0,3 µм2, площадь элементарной ячейки составляла 15 µм2. Глобальное магнитное поле, которое определяет потоки во всех сверхпроводящих контурах, было создано сверхпроводящим соленоидом.
При дисперсионных двухтональных измерениях лестничных спектров, резонанс считывающего резонатора контролировался на частоте зонда f1, а лестница возбуждалась частотой второго тона («накачка») fS. Микроволны передавались по микрополосковой линии, соединенной с Джозефсоновской лестницей и LC-резонатором. Усиленный сигнал смешивался смесителем М1 с сигналом гетеродина на частоте f2. Сигнал промежуточной частоты при 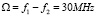 оцифровывали с помощью карты оцифровки 1Гс/с. Сигнал был умножен в цифровом виде на
оцифровывали с помощью карты оцифровки 1Гс/с. Сигнал был умножен в цифровом виде на 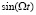 и
и 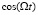 , усреднен по целому числу периодов, а его амплитуда A и фаза были извлечены. Опорная фаза (которая случайным образом изменяется, когда f1 и f2 изменяются в измерениях) была найдена с использованием аналогичной обработки малошумящего сигнала, предоставляемого микшером М2 и оцифрованного вторым каналом АЦП. Возбуждение мод приводило к изменению импеданса лестницы [8]; это изменение было зарегистрировано как сдвиг резонанса считывающего резонатора, зондированного при f1. Низкоэнергетические моды измерялись как функция потока в элементарных ячейках лестницы в диапазоне частот микроволновой установки 0,5–20 ГГц.
, усреднен по целому числу периодов, а его амплитуда A и фаза были извлечены. Опорная фаза (которая случайным образом изменяется, когда f1 и f2 изменяются в измерениях) была найдена с использованием аналогичной обработки малошумящего сигнала, предоставляемого микшером М2 и оцифрованного вторым каналом АЦП. Возбуждение мод приводило к изменению импеданса лестницы [8]; это изменение было зарегистрировано как сдвиг резонанса считывающего резонатора, зондированного при f1. Низкоэнергетические моды измерялись как функция потока в элементарных ячейках лестницы в диапазоне частот микроволновой установки 0,5–20 ГГц.
В экспериментах во временной области наблюдаются колебания Раби для «кубита», образованного лестницей и шунтирующей емкостью СК. Режимы лестничных колебаний возбуждалась коротким импульсом 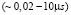 МВт на второй – тоновой частоте fS, и население возбужденного уровня было записано в конце каждого импульса; данные были усреднены по многим повторным измерениям. Время Раби для режима с минимальной энергией превысило 2μs для массивов с 92 элементарными ячейками. Это наблюдение демонстрирует, что многопереходные массивы можно рассматривать как квантовые (не ограниченные декогерентностью) системы в относительно длительном масштабе времени. Эти измерения обсудим в следующей работе, а далее сосредоточимся на спектроскопических данных.
МВт на второй – тоновой частоте fS, и население возбужденного уровня было записано в конце каждого импульса; данные были усреднены по многим повторным измерениям. Время Раби для режима с минимальной энергией превысило 2μs для массивов с 92 элементарными ячейками. Это наблюдение демонстрирует, что многопереходные массивы можно рассматривать как квантовые (не ограниченные декогерентностью) системы в относительно длительном масштабе времени. Эти измерения обсудим в следующей работе, а далее сосредоточимся на спектроскопических данных.
Результаты измерений резонансных частот для нескольких низкоэнергетических мод лестницы с r < r0 приведены на рис. 2. Номинальные параметры переходов в этой цепи были
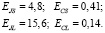
Энергии перехода, приведенные выше, были рассчитаны с использованием данных для области перехода, измеренного сопротивления испытательных переходов и соотношения Амбегаокара – Баратова. Это вычисление дает надежные значения для EJL и ECL, но значительно переоценивает значение энергии Джозефсона для меньших переходов.
Для этих параметров мы оцениваем g ≈ 0,1. Емкость заземления в этом эксперименте была 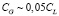 , поэтому характерная длина, обусловленная кулоновскими взаимодействиями, составляет k–1 ≈ 5×l (где l – длина элементарной ячейки). Для этих параметров можно наблюдать релятивистский спектр низкоэнергетических мод
, поэтому характерная длина, обусловленная кулоновскими взаимодействиями, составляет k–1 ≈ 5×l (где l – длина элементарной ячейки). Для этих параметров можно наблюдать релятивистский спектр низкоэнергетических мод 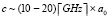 , где a0 ~ 3×l. Это привело бы к разнице частот между низшими модами
, где a0 ~ 3×l. Это привело бы к разнице частот между низшими модами 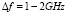 , что хорошо согласуется с наблюдениями. Сдвиг частоты (определяемый как разность между минимальной частотой моды и её частотой при Фc(0)) из-за кулоновских взаимодействий составляет приблизительно ~0,3Δf, что совместимо с малым значением k ≈ 0,2×l-1 [9].
, что хорошо согласуется с наблюдениями. Сдвиг частоты (определяемый как разность между минимальной частотой моды и её частотой при Фc(0)) из-за кулоновских взаимодействий составляет приблизительно ~0,3Δf, что совместимо с малым значением k ≈ 0,2×l-1 [9].
На панели (а) представлены данные для 24-элементной лестницы с соотношением энергий r = 3,2. Резонансные моды являются периодическими по потоку с периодом Φ0. Две критические точки расположены симметрично относительно Φ = Φ0/2. В критических точках зависимость минимального значения EJ(φ) превращается в функцию двойных минимумов; это соответствует КФП между парамагнитной и ферромагнитной фазами. Существует разница в ширине резонансов в парамагнитной и ферромагнитной фазах (показана в виде столбцов ошибок для двух точек данных).
На панели (б) показаны данные для лестницы из 92 ячеек с соотношением r = 3,2. Резонансные частоты нескольких низкоэнергетических мод показаны вблизи критической точки. С приближением к этой критической точке на Φ ≈ 0,45Φ0 наблюдается выраженное смягчение низкоэнергетических мод лестницы. Резонансы в ферромагнитной фазе достаточно широки, поэтому точность определения критических точек невелика. Положения минимумов могут быть надежно извлечены из оставшихся точек путем подбора полиномиальной кривой. Стрелки указывают на критические точки ФС(K), которые были смещены для разных режимов из-за дальнодействующих взаимодействий между элементарными ячейками массива. В пределе бесконечно длинной цепи ожидается, что критическая точка будет находиться в точке Ф = 0,46Ф0.
Частоты резонанса периодически зависят от потока. Наблюдается смягчение моды при приближении к квантовым критическим точкам, симметрично расположенным относительно потока Ф0/2. Это ключевая особенность модели Изинга в поперечном поле. Согласно этой модели, фазы с обеих сторон квантовой критической точки (квантовый парамагнетик и ферромагнетик, в терминологии спина Изинга) характеризуются различными типами возбуждений.
В парамагнитной фазе соответствующие возбуждения представляют собой колебания отдельных спинов [2]. Эти возбуждения становятся беззеркальными именно в критической точке. Напротив, возбуждения в упорядоченной (ферромагнитной) фазе являются доменными стенками (или описываются как изломы) между различными основными состояниями («вакуума»). Даже если любой сверхпроводник является бозонной системой, ожидается, что возбуждения с самыми низкими энергиями в лестницах будут иметь фермионную природу; возбуждения с более высокой энергией представляют собой составные частицы, изготовленные из этих фермионов (аналогично появлению кварков и мезонов). Появление нетривиальных возбуждений вблизи квантового фазового перехода и их свойства являются одной из главных тем будущих исследований.
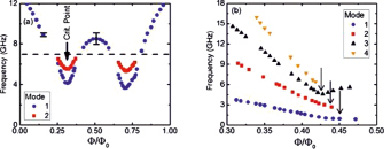
Рис. 2. Двухтональная спектроскопия низкоэнергетических внутренних мод лестниц с r ≤ r0 как функция магнитного потока в элементарных ячейках
а) б)
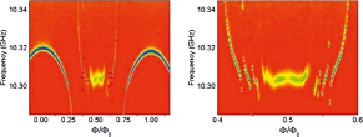
Рис. 3. Однотональные измерения для длинной (92-элементная) цепочки [панель (б) – это раздувание данных в диапазоне [0,4 < Φ/Φ0 < 0,6]
Постепенное смещение минимумов различных мод, показанных на рис. 2, б, обусловлено ненулевой ёмкостью заземления элементарных ячеек, что приводит к слабым, но не пренебрежимо малым дальнодействующим взаимодействиям между псевдоспинами. Ненулевой CG является не «ошибкой», а «особенностью»: изменение емкости заземления отдельных ячеек позволяет изготавливать устройства, характеризующиеся различными типами связи между единичными ячейками, что делает возможной эмуляцию разных квантов такие модели, как модели Изинга и XY в поперечных магнитных полях.
Точность отслеживания низкоэнергетических мод в «ферромагнитной» фазе значительно ниже, чем в «парамагнитной» фазе (рис. 2, б). На рис. 3 показано, что в однотональных измерениях с длинной цепью из 92 элементарных ячеек резонанс считывания значительно расширяется между критическими точками. По этой причине при двухтоновых измерениях нельзя точно определить положения низкоэнергетических мод для этой цепи в ферромагнитной фазе. Этот резонанс «размазывания» относится к сильному магнитному шуму в системе.
В упорядоченной (ферромагнитной) фазе влияние шума заряда на переходы между низкоэнергетическими состояниями слабее, тогда как влияние шума потока значительно сильнее, чем в неупорядоченной (парамагнитной) фазе. Отметим, что затухание пропорционально квадрату матричных элементов, так что распад из-за потока шума усиливается с коэффициентом ~106 в упорядоченной фазе, в то время как затухание из-за шума заряда снижается с коэффициентом ~103. Влияние шума заряда дополнительно подавляется небольшим фактором, который переводит матричный элемент операторов Изинга в матричный элемент физического заряда (эффект противоположен шуму потока). Сравнивая уравнения, связывающие безразмерные матричные операторы с физическим шумом, мы видим, что скорость затухания, вызванная шумом заряда, дополнительно уменьшается в фактор, 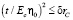 , в то время как скорость затухания шума потока повышается на коэффициент
, в то время как скорость затухания шума потока повышается на коэффициент 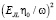 , где ω – частота моды. Это делает влияние шума потока на упорядоченной стороне перехода очень большим, в то время как влияние шума заряда остается умеренным.
, где ω – частота моды. Это делает влияние шума потока на упорядоченной стороне перехода очень большим, в то время как влияние шума заряда остается умеренным.
Избегаемые пересечения между низкоэнергетическими модами и режимом резонатора считывания четко наблюдаются в парамагнитной фазе (Φ/Φ0 < 0,45, Φ/Φ0 > 0,55), где резонанс считывания является резким (ширина резонанса Δf < 1 МГц). В ферромагнитной фазе (0,45 < Φ/Φ0 < 0,55), резонанс размыт (Δf ≈ 4 МГц) из-за переходов между низкоэнергетическими модами, вызванными шумом потока. Между ячейками Джозефсоновских массивов («спинов») можно настраивать (изменяя) энергии Джозефсона больших и меньших контактов. Эта настройка остается проблемой для других твердотельных систем [10].
Заключение
Контролируемые по замыслу взаимодействия между псевдоспинами, реализованными в виде двух состояний элементарных ячеек периодических Джозефсоновских лестниц, позволили изучить межфазные границы между упорядоченной и неупорядоченной фазами и критическое поведение, близкое к этому переходу. В частности, изучение микроволновых свойств позволило охарактеризовать низкоэнергетический спектр этой системы.
Близко к квантовому фазовому переходу, низкоэнергетические степени этой системы описываются моделью φ4 [10], которая отображает переход между упорядоченной и неупорядоченной фазами, принадлежащий классу универсальности Изинга. В модели Изинга низкоэнергетические возбуждения являются Майорановскими квазичастицами, поэтому наблюдение низкоэнергетических мод длинных лестниц можно рассматривать как прямой зонд Майорановских возбуждений в этой системе. Отметим, что, в отличие от спиновых цепочек, где с помощью методов рассеяния могут быть получены и изучены только пары Майорановских частиц, Джозефсоновские лестницы позволят нам изучить полный спектр низких энергий, в частности фермионные возбуждения.
Привлекательная аналогия обеспечивается физикой частиц, в которой фермионные возбуждения являются кварками, а пара из них соответствует пионам. По этой аналогии спектр, показанный на рис. 2, соответствует кваркам, а спектр, изученный в спиновых цепочках, пионам.
Разработанная экспериментальная платформа может помочь решить различные фундаментальные проблемы. Во-первых, в этой одномерной системе можно беспорядочно вводить беспорядок, что позволяет изучать появление промежуточных стеклообразных неэргодических фаз. Во-вторых, платформа допускает инженерные взаимодействия между псевдоспинами, которые нарушают точную интегрируемость эффективной модели Изинга, которая описывает систему в больших масштабах.
Библиографическая ссылка
Бабаян М.Г., Смирнов И.А., Черкесова Л.В., Поркшеян В.М. НОВЫЕ АППАРАТНЫЕ ПЛАТФОРМЫ ДЛЯ ИССЛЕДОВАНИЯ КВАНТОВЫХ ФАЗОВЫХ ПЕРЕХОДОВ // Международный журнал прикладных и фундаментальных исследований. 2019. № 7. С. 93-99;URL: https://applied-research.ru/ru/article/view?id=12806 (дата обращения: 07.03.2026).

