В работе [1] был предложен подход к исследованию схожести веб-сайтов с использованием Колмогоровской сложности и нормализованного расстояния сжатия. Там же был сформулирован ряд вопросов, которые требуется рассмотреть, прежде чем автоматизировать проведение больших исследований, один из которых, – можно ли выбрать наилучший архиватор и какими свойствами он должен обладать.
Основная цель данной статьи заключается в разработке методов, подходов и критериев определения наилучшего архиватора из заданного набора наиболее популярных и доступных архиваторов.
Для девяти архиваторов проведена серия экспериментов по проверке свойств так называемой «нормальности» и были оставлены четыре с наилучшими показателями выполнения этих свойств. Для этих четырех архиваторов было показано экспериментально выполнение аксиом расстояния для нормализованного расстояния сжатия.
Все этапы экспериментов были автоматизированы с помощью разработанных вспомогательных программ. С использованием программы RAR, вошедшей в четверку «нормальных», была проведена иерархическая кластеризация тестового множества сайтов компаний – разработчиков веб-сайтов, имеющая хорошую содержательную интерпретацию.
Основные понятия и инструменты
Способом описания называется произвольное вычислимое частичное отображение D из множества двоичных слов Ξ в себя [2]. Если D(y) = x, говорят, что y является описанием x при способе описания D. Для каждого способа описания D сложность относительно этого способа описания равна длине кратчайшего описания l(y): KSD(x) = min{l(y)|D(y) = x}.
Чтобы определить Колмогоровскую сложность, необходимо ввести понятие оптимального способа описания. Закономерно определить, что способ описания D1 не хуже способа описания D2, если KSD1(x) ≤ KSD2(x) + с при некотором c и для всех x.
Теорема Соломонова – Колмогорова говорит, что существует такой способ описания D, что для любого другого способа описания D' найдется такая константа c, что KSD(x) ≤ KSD’(x) + с для любого слова x [2]. Будем называть оптимальным такой способ описания, который обладает приведенным в теореме свойством. Колмогоровской сложностью слова x будем называть KSD(x), где D – оптимальный способ описания.
Теперь зафиксируем некоторый (не обязательно оптимальный) способ описания, и сложность слова x относительно этого способа описания обозначим K(x). Пусть y – еще одно двоичное слово. Обозначим K(x|y) минимальное количество битов, необходимых для восстановления x из y. Для любой пары строк x и y можно определить нормализованное расстояние сжатия (normalized compression distance, NCD) как в [3]:
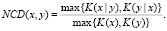 (1)
(1)
Простыми словами, если два объекта достаточно похожи, то мы можем более кратко описать один из них, учитывая информацию о другом.
Вводя расстояние NCD на множестве двоичных слов Ξ, мы тем самым определяем метрическое пространство (Ξ, NCD), если расстояние удовлетворяет трем аксиомам:
– NCD(x, y) = 0 тогда и только тогда, когда x = y (аксиома тождества),
– NCD(x, y) = NCD(y, x) (аксиома симметрии),
– NCD(x, y) ≤ NCD(x, z) + NCD(z, y) (аксиома или неравенство треугольника).
В [3] показано, что NCD, заданная формулой (1), удовлетворяет указанным аксиомам.
Колмогоровская сложность является невычислимой по Тьюрингу [2]. Поэтому на практике в качестве отображения D используются программы-архиваторы [4]. Свойства NCD, очевидно, зависят от особенностей используемого архиватора.
В соответствии с [5] определим понятие «нормального архиватора». Авторы в [5] используют термин «compressor», который мы переводим как «архиватор» (archiver), тем более что в [5] компрессор определяется как кодировщик без потерь, что более свойственно архиваторам, а не компрессорам [6]. Итак, архиватор C является нормальным, если он удовлетворяет следующим свойствам:
1) идемпотентность: C(xx) = C(x),
2) монотонность: C(xy) ≥ C(x),
3) симметричность: C(xy) = C(yx),
4) дистрибутивность: C(xy) + C(z) ≤ C(xz) + C(yz),
с точностью до аддитивного члена O(log(n)), где n – максимальная двоичная длина элемента из Ξ, включенного в рассматриваемые (не)равенства.
Теперь в формуле (1) заменим K() на C(), получая формулу
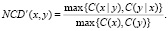 (2)
(2)
Это следует понимать в том смысле, что если два файла близки в соответствии с «теоретическим» расстоянием NCD, определяемым через Колмогоровскую сложность, то они также близки в смысле нормального архиватора. Очевидно, что для любых x и y имеем 0 ≤ NCD’ ≤ 1 + ε, представляющее, насколько различны эти два файла. Меньшие числа представляют более похожие файлы. Значение ε в верхней границе связано с деталями методов сжатия, что мы и увидим далее. В [5] доказана теорема, утверждающая, что если при вычислении NCD был использован нормальный архиватор, то такое NCD удовлетворяет аксиомам расстояния. Значит, чтобы максимально точно аппроксимировать NCD, вначале необходимо проверить существующие реальные архиваторы на «нормальность» и выбрать те из них, которые удовлетворяют его свойствам.
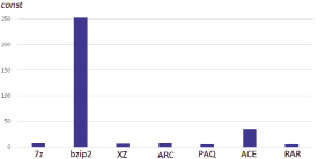
Рис. 1. Результаты проверки идемпотентности для семи архиваторов
Проверка свойств нормального архиватора
Были рассмотрены программы-архиваторы bzip2, gzip, XZ, 7z, ACE, ARC, PAQ, RAR и ZIP, выбор которых объясняется их популярностью и доступностью. Не углубляясь в детали работы архиваторов из-за недостатка места, скажем, что они могут быть разбиты на два семейства, – потоковые и блочные, – алгоритмы работы которых существенно различны [6].
В качестве объектов для экспериментов были выбраны первые страницы 30 различных сайтов в формате html. Среди них есть сайты вузов, факультетов СПбГУ, научных, коммуникационных и торговых площадок, а также сайты коммерческих компаний: www.amursu.ru, jf.spbu.ru, arxiv.org, www.amazon.com, amdm.ru, www.instagram.com, ok.ru и др.
Все этапы экспериментов были автоматизированы с помощью разработанных вспомогательных программ для скачивания первых страниц сайтов в формате html, создания конкатенаций файлов, сжатия файлов различными архиваторами и вычисления нормализованного расстояния сжатия.
В разделе 1 сказано: свойство идемпотентности для нормального архиватора должно выполняться с требуемой точностью, а именно C(xx)-C(x) = O(log)n)). Если это свойство выполняется, то разность между длиной сжатой версии файла и длиной сжатой версии конкатенации этого файла с самим собой должна быть ограничена сверху функцией const*log(n), где const – константа, а n – размер файла: C(xx)-C(x) ≤ const*O(log)n)). Поэтому для проверки идемпотентности и сравнения результатов будем рассматривать эту разность для каждого объекта и будем делить её на log(n):
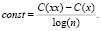
Тогда чем больше эта константа, тем хуже выполняется проверяемое свойство. На рис. 1 представлена диаграмма средних значений const, вычисленных по описанному выше способу, по которой можно судить о выполняемости идемпотентности различными архиваторами; zip и gzip отсутствуют на диаграмме (значения const > 1500).
Любой архиватор должен обладать свойством монотонности, по крайней мере c требуемой точностью. Это свойство очевидно для потоковых архиваторов и лишь немного менее очевидно для блочных архиваторов, поэтому отдельную проверку проводить нецелесообразно.
Для проверки симметричности будем по аналогии с предыдущей проверкой вычислять константу, определяющую точность выполнения свойства как отношение разности между длинами симметричных конкатенаций файлов к логарифму от длины одного из этих файлов.
Известен теоретический факт, что потоковые компрессоры не являются абсолютно симметричными, что с особенностями сжатия: исходный файл может иметь закономерности, к которым адаптируется архиватор; однако после пересечения границы между файлами внутри конкатенации он должен «отучиться» от этих закономерностей и приспособиться к закономерностям второго файла [5–7]. Это определяет в свойстве симметрии неточность, которая асимптотически уменьшается с длиной файла. Для архиваторов, основанных на блочном кодировании, симметричность выполняется более строго, поскольку они анализируют каждый входной блок, учитывая все особенности внутри него для получения сжатой версии. Сказанное подтверждается нашими экспериментами. На рис. 2 показаны средние константы по всем конкатенациям файлов для рассматриваемых архиваторов.
Из диаграммы видно, что худшей симметричностью обладают потоковые архиваторы gzip и zip. Наилучший (практически нулевой) результат у блочного архиватора bzip2, что подтверждает теоретический факт, описанный выше.
Свойство дистрибутивности архиватора не сразу интуитивно понятно. Рассмотрим сначала случай, при котором все три файла, участвующие в неравенстве, различны. В этом случае эксперименты показали, что все рассматриваемые архиваторы удовлетворяют неравенству дистрибутивности при всех возможных комбинациях файлов, на которых мы проверяем данное свойство. Теперь предположим, что какие-либо два из трех файлов в неравенстве одинаковы. При этом возможны три варианта:
1) x = y – в этом случае неравенство получается следующим: C(xx) + C(z) ≤ C(xz) + C(xz) и неравенство справедливо, если компрессор C удовлетворяет свойствам идемпотентности и монотонности;
2) y = z – в этом случае получившееся неравенство справедливо при условии идемпотентности компрессора C: C(xy) + C(y) ≤ C(xy) + C(yy);
3) x = z – при этом получившееся неравенство аналогично предыдущему при условии симметричности компрессора C: C(xy) + C(x) ≤ C(yx) + C(xx).
Сведем результаты экспериментов в табл. 1 с условными обозначениями: « + » обозначает хорошее выполнения свойства архиватором, « + /–» удовлетворительное, а «–» – невыполнение свойства. Свойствами нормального архиватора обладают четыре архиватора: 7z, XZ, PAQ и RAR.
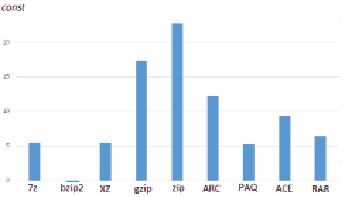
Рис. 2. Результаты проверки симметричности
Выполнение свойств нормального архиватора
|
7z |
Bzip2 |
XZ |
Gzip |
Zip |
ARC |
PAQ |
ACE |
RAR |
|
|
Идемпотентность |
+ |
– |
+ |
– |
– |
+ |
+ |
+ /– |
+ |
|
Монотонность |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Симметричность |
+ |
+ |
+ |
+ /– |
+ /– |
– |
+ |
+ /– |
+ |
|
Дистрибутивность |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
Проверка аксиом расстояния для NCD
Аксиомы расстояния были проверены для NCD, вычисляемого по формуле (2) с использованием четырех «нормальных» архиваторов. Для всех четырех случаев все три аксиомы выполняются с требуемой точностью. Покажем это на примере второй аксиомы расстояния, суть которой заключается в том, что расстояние от объекта x до объекта y должно быть равно расстоянию в обратном направлении. Для проверки этой аксиомы рассматривалась разность между этими расстояниями для каждой пары объектов из выборки, использованной в разделе 2, и вычислялось по модулю среднее отклонение по каждому архиватору. На рис. 3 представлена диаграмма, отображающая результаты экспериментов, из которой видно, что все рассматриваемые архиваторы удовлетворяют второй аксиоме расстояния с приблизительно равной точностью.
В практическом плане можно говорить о правильности результатов экспериментов для нормальных архиваторов 7z, XZ, PAQ и RAR, поскольку уже упомянутая теорема из [5] утверждает, что если при вычислении NCD был использован нормальный архиватор, то такое NCD удовлетворяет аксиомам расстояния.
Пример кластеризации сайтов с помощью NCD
Здесь приводится пример кластеризации сайтов на основе матрицы расстояний, построенной для NCD c использованием нормального архиватора RAR. Взято 15 сайтов четырех популярных компаний по созданию сайтов в Рунете (преимущественно интернет-магазины и корпоративные сайты). Проверялось предположение о том, что у каждой компании по созданию сайтов есть свой стиль, и тогда это будет видно по результатам кластеризации. На рис. 4 приводится дендрограмма результатов кластеризации.
На рисунке указаны порядковые номера сайтов из выборки, их доменные имена и компании-разработчики. Заметно, что все сайты разделились на четыре кластера, причем сайты, разработанные одной компанией, преимущественно содержатся в одном кластере. Исключения подтверждают правило – сайт под номером 11 компании «Медиасфера» по своей структуре действительно больше похож на сайты компании ARTW, в чем можно убедиться визуально, посмотрев сайты.
Результаты кластеризации позволяют сделать вывод, что у каждой компании, разрабатывающей сайты, есть некоторый свой стиль построения сайта. Возможно, в каждой компании используются свои шаблоны, на основе которых в последующем разрабатывается сайт.
Заключение
В статье подробно исследован вопрос о том, какими свойствами должен обладать архиватор (как практический аналог Колмогоровской сложности) и каким образом выбрать наилучший из множества архиваторов. Сформулированы четыре свойства такого нормального архиватора и три аксиомы NCD, вычисляемого с помощью такого архиватора.
Проведена серия экспериментов, позволивших из девяти популярных и доступных архиваторов выбрать четыре, обладающих требуемыми свойствами нормальности. Показано, что аксиомы расстояния выполняются для NCD, вычисляемого этими четырьмя архиваторами.
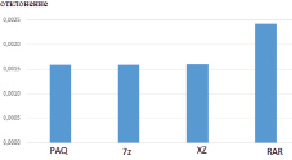
Рис. 3. Результаты проверки аксиомы симметрии
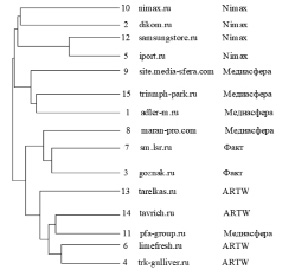
Рис. 4. Дендрограмма кластеризации по методу ближайшего соседа
С использованием одного из нормальных архиваторов, а именно RAR, показана возможность кластеризации выборочного множества сайтов, имеющая хорошую содержательную интерпретацию.
Библиографическая ссылка
Печников А.А., Прусский Д.А. ПРОГРАММЫ-АРХИВАТОРЫ ДЛЯ ВЫЧИСЛЕНИЯ КОЛМОГОРОВСКОЙ СЛОЖНОСТИ // Международный журнал прикладных и фундаментальных исследований. 2019. № 7. С. 118-123;URL: https://applied-research.ru/ru/article/view?id=12810 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/mjpfi.12810

