Специфика лазерного облучения тонких пленок состоит прежде всего в том, что мишень представляет собой двух-, трехкомпонентную систему, состоящую из материалов с различными оптическими свойствами. Подводимая энергия в зависимости от длины волны поглощается в различных слоях в соответствии с их оптическими свойствами и перераспределяется между пленками и подложкой согласно теплофизическим свойствам материалов и длительностью облучения. Эти особенности определяют различие в режимах нагрева пленок при взаимодействии импульсов лазерного излучения различной длительности.
В информационных технологиях известно, что пленки аморфных молекулярных полупроводников [1] и пленки полимерных композиций с наночастицами [2] в последнее время становятся оптимальным фототермопластическим (ФТП) материалом для прикладной голографической интерферометрии, а также в молекулярной электронике [3]. Эти пленки при поглощении света используемого лазерного излучения, обладая низкой электропроводностью и высокой фотопроводимостью, легко деформируются выше температуры размягчения [4].
Способы записи информации на таких пленках имеют две особенности: создание электрического поля, соответствующего распределению интенсивности света при экспонировании в регистрирующем слое, и тепловое проявление, при котором под действием кратковременного теплового импульса температура регистрирующего слоя повышается до температуры размягчения, и электростатические силы деформируют его поверхность в соответствии с распределением электростатического поля на ней, образуя голограмму, которая вновь стирается нагревом регистрирующего слоя на несколько градусов выше температуры размягчения.
Этап проявления скрытого электростатического изображения путем нагрева реверсивного носителя является наиболее специфичным. Эффективность его зависит от реологических и диэлектрических свойств регистрирующей среды. Существует несколько способов нагрева органических фотополимеров:
а) теплом, выделяемым при пропускании постоянного и переменного тока через элементы матрицы сопротивлений разной конфигурации, нанесенные на стеклянную подложку;
б) теплом, идущим от внешнего источника тепла;
в) теплом, выделяемым при пропускании токов высокой частоты через металлизированный подслой на стекле;
г) теплом, выделяемым при взаимодействии инфракрасного лазерного излучения с реверсивным носителем.
Как известно, для организации локальной, плотной и оперативной записи информации большое преимущество перед другими способами имеет проявление записи голограмм через нагрев регистрирующего слоя ИК лазерным излучением. Однако существующие носители имеют структуру ФТП пленка + металлический слой + подложка. Лазерный нагрев пленки в такой структуре рассмотрен в работе [5]. Если здесь металлический слой необходим для организации токового нагрева, то при лазерном нагреве надобность нанесения этого слоя отпадает. Тогда фототермопластический носитель (ФТПН) становится двухслойной структурой ФТП пленка+подложка. Такая структура экономически дешевле, технологически проста и увеличивает плотность записи до 30 процентов за счет площади удаленных токопроводящих слоев, а также исчезают технологические узлы, управляющие режимами включения и выключения тока, осуществляющего нагрев пленки. Но это обстоятельство требует пересмотра условий лазерного нагрева ФТП пленки. Качество записи голограмм на ФТПН определяется оптимальным преобразованием скрытого электростатического изображения в механический рельеф, который образуется в результате нагревания ФТП слоя до температуры размягчения Тр. Незначительное отклонение температуры проявления от оптимального значения Тр влечет за собой резкое падение дифракционной эффективности. Например отклонение температуры на 2 °С приводит к падению дифракционной эффективности голограмм на 50 % [6].
Это обстоятельство выдвигает особые требования к регулированию мощности лазерного источника – она должна быть определена для оптимального нагрева с заданной температурой размягчения Тр ФТП слоя. Следовательно, главная задача регистрации информации на ФТПН при проявлении излучением инфракрасных лазеров сводится к определению зависимости температуры поверхности ФТПН от параметров нагревающего лазера, а также от оптических и теплофизических параметров ФТПН. Кроме того, необходимо исследовать особенности развития тепловых полей ФТПН в зоне нагрева при различных формах и длительностях импульса нагрева.
Нагрев тонкой пленки, нанесенной на диэлектрическую подложку, рассматривался рядом авторов [7–9]. Основные физические процессы, протекающие при воздействии лазерного излучения на такую структуру, рассматриваются в работе [7], где обращается внимание как на материал пленки, так и на его оптические свойства.
Исследован нагрев тонких пленок в одномерном случае лазерным излучением в видимом и ИК диапазоне с плотностями потока I < 106 вт/см2, при которых пленки термически разрушаются. В [8] решается одномерная и двумерная задача нагрева металлической тонкой пленки, нанесенной на диэлектрическую подложку. Температура нагрева пленки и подложки находятся путем решения системы уравнений теплопроводности при помощи преобразований Лапласа. В [9] задача определения температуры нагрева решается методом разложения в ряды по малому параметру. Однако во всех этих работах рассмотрен случай, когда нагреваемая пленка непрозрачна, а подложка прозрачна для облучаемых волн. В то же время, как показано в [10], большинство ФТП пленок в ИК области излучения являются практически прозрачными и их нагрев для проявления записи информации становится возможным только через нагрев поглощающей излучение подложки. Поэтому результаты [8–9] для этого случая становится непригодными и в настоящей работе рассматривается вариант, когда нагрев ФТП пленки осуществляется через поглощающие излучения подложки.
Цель работы: анализ процесса нагрева ФТП пленки через подложку при нагреве излучением лазера.
Нагрев пленки
Пусть регистрирующий информацию ФТП слой нанесен равномерно на диэлектрический носитель и находится в идеальном тепловом контакте с подложкой. Их теплофизические и оптические параметры не зависят от температуры и от интенсивности облучения.
Тонкая ФТП пленка предполагается прозрачной для данной длины волны облучения, и к концу импульса излучения пленка прогревается довольно равномерно за счет теплопроводности, т.е.
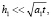 (1)
(1)
где a1 – коэффициент теплопроводности материала пленки, t – длительность импульса излучения. За это время подложка прогреется на глубине 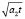 , которая намного меньше, чем ее толщина, т.е. имеет место
, которая намного меньше, чем ее толщина, т.е. имеет место 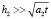 , (a2 – температуропроводность подложки). Это обстоятельство дает основание рассматривать подложку как полубесконечное тело.
, (a2 – температуропроводность подложки). Это обстоятельство дает основание рассматривать подложку как полубесконечное тело.
Предположим, что в такой системе на поверхности ФТП пленки записывается голограмма с радиусом rH, которую надо нагревать излучением до температуры размягчения, при котором образуется деформированная поверхность согласно записанной на голограмме информации и происходит процесс ее фиксации. С этой целью вся площадь голограммы облучается со стороны пленки аксиально симметричным потоком излучения, интенсивность которого w(r) зависит только от радиуса r. Процесс превращения световой энергии в тепловую описывается функциями тепловыделения в пленке
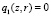 ,
,
так как она прозрачна, а в подложке
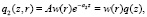 (2)
(2)
где 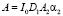 , D1 – коэффициент пропускания пленки, A2 – поглощательная способность, α2 – коэффициент поглощения подложки; функция w(r) описывает радиальное распределение интенсивности, явный вид рассматривается ниже; ослабление светового потока по оси z описывается законом Бугера – Ламберта. I0 – интенсивность излучения в точке z = r = 0.
, D1 – коэффициент пропускания пленки, A2 – поглощательная способность, α2 – коэффициент поглощения подложки; функция w(r) описывает радиальное распределение интенсивности, явный вид рассматривается ниже; ослабление светового потока по оси z описывается законом Бугера – Ламберта. I0 – интенсивность излучения в точке z = r = 0.
При этих условиях искомая температура размягчения T1 ФТП пленки находится из решения двухмерной системы уравнений теплопроводности следующего вида:
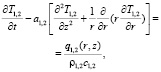 (3)
(3)
где ρ – плотность, с – теплоемкость, индексы 1, 2 относятся к параметрам пленки и подложки соответственно; 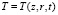 .
.
Задача решается при следующих граничных и начальных условиях:
z = 0 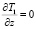 ,
,
z = h T1 = T2, 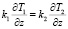 ,
,
z = ∞ r = ∞ T1 = T2 = 0,
t = 0 T1 = T2 = 0.
Применим к (3) интегральное преобразование Ханкеля нулевого порядка по координате r и преобразование Лапласа по времени t. Для трансформанта температуры 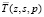 (s и p-параметры интегральных преобразований соответственно Ханкеля и Лапласа) получим систему уравнений
(s и p-параметры интегральных преобразований соответственно Ханкеля и Лапласа) получим систему уравнений
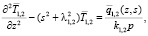 (4)
(4)
где
 ,
,
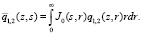 (5)
(5)
Решая систему (4), для изображений температуры ФТП пленки 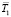 находим
находим
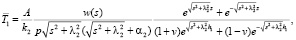 (6)
(6)
где
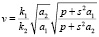 и
и 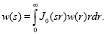 (7)
(7)
Если учитывать, что ширина луча имеет размер голограммы и она много больше, чем толщина пленки (т.е. 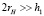 ), то для размера голограммы выполняется неравенство
), то для размера голограммы выполняется неравенство
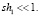 (8)
(8)
Используя условие (8) в совокупности с условием (1), получим вместо (6) следующее выражение для 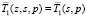 :
:
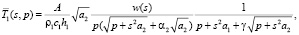 (9)
(9)
где 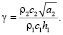
Оригинал выражения (9) можно найти, разлагая изображение на простые дроби после использования теоремы смещения. Используя таблицу оригиналов, выполняя ряд операций и вычисляя интегралы, получим оригинал по параметру р в следующем виде:
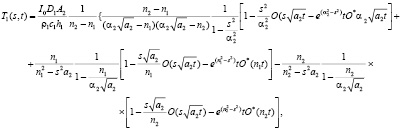 (10)
(10)
где
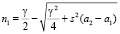 ;
; 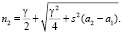 (11)
(11)
Окончательное решение задачи находится с помощью обратного преобразования Ханкеля
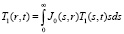 , (12)
, (12)
что вычисляется численным методом.
Однако при малых временах (p → ∞) облучения можно получить аналитические выражения для температуры пленки. Это связано с применением условия (8). При малых толщинах пленки и когда радиус голограммы 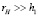 , в знаменателе выражения (9) можно пренебречь слагаемым s2ai (i = 1,2) по сравнению с величиной p, которое имеет большие значения при малых t. Тогда вместо (9) имеем
, в знаменателе выражения (9) можно пренебречь слагаемым s2ai (i = 1,2) по сравнению с величиной p, которое имеет большие значения при малых t. Тогда вместо (9) имеем
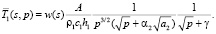 (13)
(13)
Переходя к оригиналам по параметрам p, используя таблицы [10], и по s с помощью обратного преобразования Ханкеля находим
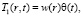 (14)
(14)
где
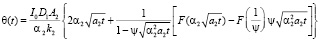 , (15)
, (15)
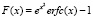
описывает температуру пленки, зависящую только от времени облучения.
Параметр 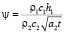 – показывает темп нагрева пленки.
– показывает темп нагрева пленки.
Следует отметить, что выражение (15) является решением одномерной задачи, которое получается из (2), если при выполнении условия (8) пренебречь радиальным изменением температуры и функцию распределения интенсивности считать равномерным по всей поверхности голограммы.
Как правило, для тонких пленок параметр 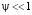 (например, для ФТП пленок на стеклянной подложке имеет место ρ1 < ρ2 c1 < c2 для времен, определенных выражением
(например, для ФТП пленок на стеклянной подложке имеет место ρ1 < ρ2 c1 < c2 для времен, определенных выражением 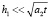 ). Тогда приведя выражение (15) к более простому и удобному для практического применения виду, для (14) имеем
). Тогда приведя выражение (15) к более простому и удобному для практического применения виду, для (14) имеем
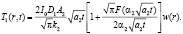 (16)
(16)
Из (14) и (16) следует, что при малых временах учет радиального распределения интенсивности облучения приводит к тому, что характер радиального распределения температуры на поверхности голограммы прямо зависит от поведения функции w(r). В большинстве случаев радиальное распределение интенсивности источников лазера описывается функцией Гаусса [11]
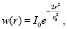 (17)
(17)
где r0 – полуширина пучка на плоскости голограммы, и она связана с полной выходной мощностью лазера Р0 выражением 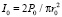 , где
, где 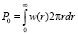 .
.
Как видно из (17), при r = r0 интенсивность пучка в е2 раз меньше, чем в центре. Это означает, что температура в центре голограммы в е2 раз больше, чем температура на краю голограммы. Это обстоятельство крайне отрицательно влияет на качество проявления записи оптической информации, так как дифракционная эффективность на поверхности голограммы будет разной. Поэтому одной из главных задач использования лазеров для нагрева с целью проявления голограммы является получение равномерного освещения поверхности голограммы. Существуют разные способы, например метод записи информации в стадии остывания пленки, когда на поверхности температура относительно выравнивается [12–13].
Но наиболее эффективным является использование фильтров с таким пропусканием, чтобы интенсивность прошедшего излучения в любой точке сечения пучка была такой же, как и на краю [14–15]. Для этого пропускание фильтра по интенсивности должно иметь вид
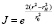 при r ≤ rH и
при r ≤ rH и 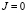 при r > rH.
при r > rH.
Тогда полную мощность для равномерного освещения всей поверхности голограммы получаем из произведения
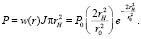
Дифференцируя по rH, находим максимальную полезную для равномерного нагрева мощность, которая равна 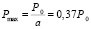 .
.
Отсюда следует, что при изменении гауссового пучка на равномерно освещающий пучок выравнивающим фильтром общая мощность источника падает в «е» раз, что следует учитывать в расчетах.
Рассмотрим частные случаи выражения (16). Во многих случаях весьма часто в качестве подложки используются стеклянные или керамические материалы, т.е. диэлектрики с коэффициентом поглощения a2~1–102см-1. Для таких материалов выполняется условие 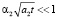 вплоть до времен t~10-3c, когда
вплоть до времен t~10-3c, когда 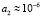 м2/с. При этих условиях выражение (16) можно привести к виду
м2/с. При этих условиях выражение (16) можно привести к виду
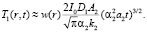 (18)
(18)
Знание температурного поля материала при воздействии лазерного излучения позволяет определить необходимые критические плотности потока излучения, падающего за данный промежуток времени t на поверхность ФТП материала для достижения заданной расчетной температуры Тр. Например, используя (18), можно получить соотношения для расчета интенсивности, требуемой для получения на поверхности ФТП материала температуры размягчения Тр
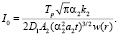 (19)
(19)
Наоборот, при постоянной интенсивности источника излучения можно найти необходимый интервал времени для достижения на поверхности материала температуры размягчения Тр:
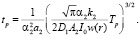 (20)
(20)
Необходимый для достижения на поверхности материала заданной температуры Тр, временной интервал определяется теплопроводностью и коэффициентом поглощения материала, а также зависит от площади облучаемой поверхности и уменьшается с ростом плотности потока и поглощающей способности материала.
Для быстрого нагрева ФТП пленки необходимо ее наносить на поверхность металла, где коэффициент поглощения имеет порядок a2~105–106 см-1. тогда из (16) при 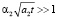 имеем
имеем
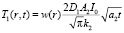 , (21)
, (21)
т.е. в прикладных работах при подборе подложки следует учитывать, что из сравнений (16) и (21) температура ФТП пленки на металлических подложках изменяется по закону t1/2, в то время как на диэлектрических подложках как t3/2. Это означает, что нагрев на металлических подложках осуществляется гораздо быстрее, чем нагрев ФТП пленки на диэлектрических подложках.
Выводы
Приведенные выше расчеты показывают, что при малых временах излучения с гауссовым распределением интенсивности поверхность голограммы нагревается неравномерно, что объясняет причину быстрого изнашивания центральной части голограммы при реверсивной записи информации. Найденные выражения позволяют находить оптимальные условия проявления записи голограммы в рассматриваемых случаях.
Анализ показал, что неравномерный нагрев наиболее эффективно можно устранить, используя фильтры с таким пропусканием, чтобы интенсивность прошедшего излучения в любой точке сечения пучка была такой же, как и на краю.
Рассмотрены различные предельные случаи и найдены выражения для определения пороговой мощности и времени нагрева для достижения температуры размягчения.
Знание температурного поля материала при воздействии лазерного излучения позволяет определить необходимые критические плотности потока излучения, падающего за данный промежуток времени t на поверхность ФТП материала для достижения заданной расчетной температуры.
Библиографическая ссылка
Джаманкызов Н.К., Акимжанова Ч.С., Исманов Ю.Х. О НАГРЕВЕ ФОТОТЕРМОПЛАСТИЧЕСКОЙ ПЛЕНКИ ЧЕРЕЗ ПОГЛОЩАЮЩУЮ ПОДЛОЖКУ ЛАЗЕРНЫМ ПУЧКОМ С ГАУССОВЫМ ПРОФИЛЕМ // Международный журнал прикладных и фундаментальных исследований. 2019. № 7. С. 130-135;URL: https://applied-research.ru/ru/article/view?id=12812 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/mjpfi.12812

