В настоящее время активно развивается направление создания многоразовых космических ракет-носителей [1–3]. Возвращаемая и повторно используемая первая ступень позволяет удешевить доставку полезной нагрузки на космическую орбиту. Мягким приземлением называется такое приземление, когда касание поверхности Земли происходит с нулевой или с некоторой небольшой скоростью, при которой сохранится конструкция и работоспособность спускаемой ступени. Вопросам оптимизации управления посадкой космических аппаратов посвящены многие работы.
В работе [4] был проведен численный эксперимент по получению оптимальной траектории на последнем вертикальном участке приземления с использованием принципа максимума Понтрягина. Численный метод, использованный при этом – метод пристрелки, работоспособность которого для задач оптимального управления с переключением показана в [5] и [6]. В данной работе проводится анализ влияния отклонения некоторых параметров от расчетных значений (вызванных случайными факторами) на возможность осуществления мягкой посадки.
Проблемам решения задачи мягкой посадки посвящены работы как зарубежных авторов [7, 8], так и российских ученых [9–11].
Постановка задачи и математическое моделирование процесса посадки
Система уравнений движения возвращаемой ступени ракеты в вертикальной плоскости:
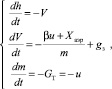
где h – расстояние от космического аппарата до поверхности (м), V – скорость космического аппарата (м/сек), m – масса космического аппарата (кг), GT – расход топлива (кг/сек), gЗ – ускорение свободного падения на Земле (м/с2), βu = P – тяга двигателя (Н), β – удельный импульс двигателя (м/с), Xаэр = СxρhV2S/2 – аэродинамическое сопротивление (Н), ρh – плотность воздуха, зависящая от высоты, Cx – коэффициент аэродинамического сопротивления, S – площадь миделя спускаемой ступени.
Интегрирование проводится методом Рунге – Кутты 4-го порядка с шагом по времени 0,01 с. Из результатов расчета работы [4] взяты данные по начальным значениям высоты, скорости и массы ступени в момент включения двигателя, а также все значения величин, участвующих в расчете.
За случайные величины, распределенные по нормальному закону распределения, принимаем следующие параметры: скорость в момент включения двигателя, масса и высота в момент включения двигателя, удельный импульс, расход двигателя, а также плотность воздуха и коэффициент аэродинамического сопротивления. Количество испытаний в методе Монте-Карло N = 1000. Интегрирование ведется до момента достижения высоты или скорости нулевого значения с заданной точностью ε = 0,001 (м или, соответственно, для скорости м/с). В случае достижения нулевой скорости ранее, чем нулевой высоты, моделируем отключение двигателя и свободное падение ступени с полученной высоты.
Величина скорости при достижении уровня земли будет представлять случайную величину, для которой рассчитываются:
– математическое ожидание
,
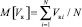– дисперсия
,
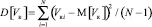– среднеквадратическое отклонение
,
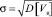– коэффициент асимметрии
,
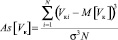– коэффициент островершинности
.
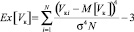Отклонения случайных величин в каждом испытании формируются при помощи датчика случайных чисел. В силу того, что программирование велось на языке ФОРТРАН, стандартное нормальное распределение было получено из равномерного распределения на интервале от 0 до 1 (встроенная подпрограмма Random) следующим образом: полученные датчиком случайных чисел две равномерно распределенные случайные величины Xi равн, Yi равн соответствуют двумерному равномерному распределению с плотностью распределения равным 1. После пересчета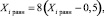 
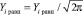, производится выбор: если 
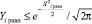, то Xi станд = Xi равн, иначе значение Xi равн отбрасывается. Полученный таким образом массив случайных чисел Xi станд соответствует нормальному стандартному распределению N.
Дальнейший пересчет значений случайных величин проводился по формуле: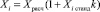 
, где Xi – рассматриваемый в качестве случайной величины параметр, Xi станд – величина, полученная датчиком случайных чисел для стандартного нормального распределения, Xрасч – расчетное значение параметра, k – коэффициент, задающий максимальное отклонение случайной величины от расчетного значения, соответствует 3σ.
Результаты расчетов
Для расчетов приземления спускаемого аппарата были взяты исходные данные, приблизительно соответствующие характеристикам ракеты Falcon 9, а также из результатов работы [4].
Значения переменных, соответствующие моменту включения двигателя: H(0) = 448,0558 м;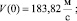 
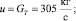m(0) = 20 т; 
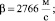Сx = 0,8.
В качестве зависимости плотности воздуха от высоты в стандартных условиях была принята следующая аппроксимация, дающая удовлетворительную точность до высоты в 20 км:
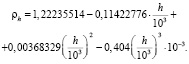
Вначале было проанализировано влияние на скорость приземления всех выбранных случайных величин по отдельности. Принималось отклонение от расчетных для каждой случайной величины в пределах ±1 %, что соответствовало нормальному распределению в пределах ±3σ. Параметры статистического распределения скорости приземления приведены в табл. 1. Приведены значения математического ожидания, среднеквадратичного отклонения, коэффициента асимметрии и коэффициента островершинности.
Влияние совместного отклонения всех рассматриваемых случайных величин на распределение конечной скорости представлено в табл. 2 и рис. 1, рис. 2.
При этом принимались следующие возможные отклонения по параметрам: β(±5 %), σh(±2 %), H(0) (±2 %), V(0) (±0,1 %), Сх (±2 %), m(0) (±1 %), u(±0,5 %). Предполагаем, что включение двигателя осуществляем по достижению расчетной скорости, тогда разброс по начальной скорости минимален, соответствует точности измерений.
На рис. 1 представлен полигон распределения скорости приземления, построенный по средним значениям интервалов распределения (число которых выбиралось равным 20), соответствует статистической плотности вероятности.
Таблица 1
Влияние на скорость приземления некоторых параметров
|
Случайные величины |
M[Vk] |
σ[Vk] |
As |
Ex |
|
Импульс двигателя, β |
6,356695 |
3,258635 |
0,82478 |
0,590076 |
|
Плотность воздуха, ρh |
2,938269 |
0,546773 |
–0,56457 |
0,553074 |
|
Высота включения двигателя, H(0) |
6,057671 |
3,003891 |
0,784137 |
0,667651 |
|
Скорость включения двигателя, V(0) |
7,728864 |
4,086735 |
0,966195 |
1,05187 |
|
Сх |
2,956057 |
0,582367 |
–0,79403 |
1,448599 |
|
Масса, m(0) |
6,623025 |
3,439914 |
0,849341 |
0,852846 |
|
Расход топлива, u |
6,51975 |
3,446187 |
0,748269 |
0,330196 |
Таблица 2
Параметры распределения скорости приземления при совместном отклонении рассматриваемых случайных величин
|
Параметры распределения скорости приземления |
M[Vk] = 6,51975 |
σ [Vk] = 3,446187 |
As = 0,748269 |
Ex = 0,330196 |
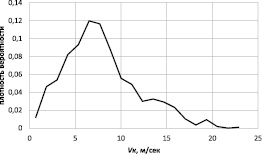
Рис. 1. Плотность распределения случайной величины Vk
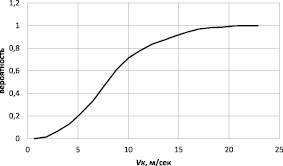
Рис. 2. Функция распределения случайной величины Vk
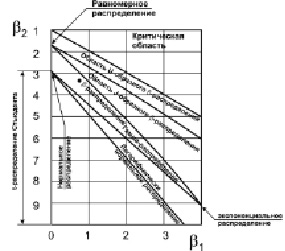
Рис. 3. Кривые Пирсона с указанным точкой полученным распределением случайной величины Vк . Здесь β1 = As, β2 = Ex + 3
На рис. 2 представлена статистическая функция распределения случайной величины Vк при совместном возможном случайном отклонении рассмотренных параметров от расчетных значений (принятых или полученных в процессе расчета в [4]). Следует отметить, что в авиации мягкой посадкой принято считать касание поверхности земли с вертикальной скоростью меньшей 2 м/с. Для первой ступени ракеты Falcon 9 ограничение по скорости приземления в открытых источниках указано 6 м/с.
На рис. 3 в поле кривых Пирсона приведена точка, соответствующая характеристикам полученного распределения.
Заключение
Анализ результатов расчета показывает, что вероятность мягкой посадки без использования обратной связи в управлении тягой двигателя (даже при малых случайных отклонениях рассмотренных параметров) чрезвычайно мала. Так, вероятность того, что при малых отклонениях рассматриваемых случайных величин от расчетных значений скорость приземления будет меньше 2 м/с, равна 2 %, вероятность того, что скорость приземления будет меньше 5 м/с, равна 20 %.
При выбранной программе управления тягой двигателя (включение при достижении расчетного значения скорости приземления и выключение при достижении скорости или высоты нулевого значения без возможности дросселирования двигателя) скорость приземления, как случайная величина, имеет несимметричное распределение, достаточно сильно отличающееся от нормального.
Необходима разработка управления тягой двигателя с обратной связью при выбранном законе оптимального управления на последнем вертикальном участке приземления.
Библиографическая ссылка
Мозжорина Т.Ю., Осипов В.В. ВЕРОЯТНОСТНЫЙ АНАЛИЗ ВОЗМОЖНОСТИ МЯГКОГО ПРИЗЕМЛЕНИЯ НА ПОСЛЕДНЕМ ВЕРТИКАЛЬНОМ УЧАСТКЕ РАБОТЫ ДВИГАТЕЛЯ // Международный журнал прикладных и фундаментальных исследований. 2019. № 7. С. 136-140;URL: https://applied-research.ru/ru/article/view?id=12813 (дата обращения: 03.04.2025).
DOI: https://doi.org/10.17513/mjpfi.12813