С ходом развития корпоративных информационных систем [1] осуществляется активное внедрение систем документооборота в работу государственных и частных проектных и кадастровых организаций, в частности бюро технической инвентаризации (БТИ).
Введение таких систем позволяет упростить оперирование проектной документацией различного рода недвижимости, подлежащей государственной регистрации и наличию технического паспорта. Это касается как автоматизации задания параметров и сооружений при их регистрации, так и дальнейшего администрирования работы с такими проектами, сводящегося к адаптивной разработке технических паспортов на новые сооружения, так и выполнения поиска документов при соответствующих кадастровых запросах.
Проведение местных измерений кадастровой инвентаризации связано с оперированием значительного числа параметров объекта недвижимости, часть из которых может быть определена с учетом обработки некоторого подмножества остальных, как, например, географические координаты участков или объемные характеристики помещений [2]. Проработка шаблона для внесения определяющих объекта характеристик, с учетом исключения смежных параметров, нахождение которых было бы возможно при дальнейшем анализе данных и использовании соответствующих математических вычислений, позволило бы сократить общий объем местных работ инженеров по измерению и фиксации. Последнее означает, помимо достижения общей эргономики труда, также и минимизацию возможных ошибок внесения параметров, за счет сокращения оперируемых специалистом данных.
Проблематика данной задачи представляет поиск и математическое обоснование шаблонов фиксации исходных данных [3, 4], постобработка которых представила бы полный документ по объекту, исключающий необходимость в проведении дополнительных измерительных работ. Решение сводится к уместному исключению описательных параметров документа за счет рассмотрения возможностей перерасчета характеристик и их взаимного отношения. Результирующие шаблоны будут иметь исключительно частный характер содержания под конкретный объект недвижимости. Допускается формализация определения наследования характеристик шаблонов между объектами, что представит отдельное направление исследование настоящей задачи.
Материалы и методы исследования
С точки зрения математики рассматриваемая проблема представляет собой комбинаторную задачу оптимизации наборов векторов параметров объекта. С другой стороны, определяющим фактором будет снижение общей «сложности» работ местной фиксации шаблона, выраженной в сумме соответствующих эмпирических параметров по каждому из параметров измерения, заданных заранее. Такая функция «сложности» означает вариацию размерностью задачи, однако меньшее количество параметров не может гарантировать оптимальность оперирования с первичным документом, поэтому в настоящем под критерием оптимального поиска будем понимать не количество параметров, а функцию, отражающую физические затраты по их общей фиксации [5].
Обозначим задачу математически, дополнив описанное выше соответствующими отношениями связи. Так, пусть:
P = {pi} вектор параметров измерения шаблона, 1 ≤ i ≤ N и N их общее количество;
C(P, N) – функция затрат на работы по измерению и внесению параметров {P, N} в шаблон. Как и было указано ранее, представляет заранее определенный набор эмпирических величин сi для каждого pi:
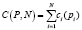
Inf = Inf(P, N) – функция информативности шаблона, представляющая зависимость от его параметров P и их общего количества N. Частными характеристиками такой функции будут Iш, Pш и Nш – показатели для полного документа кадастрового объекта. Также представляет сумму собственных значений infi по каждому из входящих в нее параметров pi:
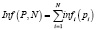 .
.
M = (mi,j) – матрица размерностью [Nш×Nш] отношений параметров {p}, отражающая возможность представления или ее отсутствия (m i,j = –∞) между парными наборами i-й и j-й характеристик объекта недвижимости.
Логика поставленной проблемы подразумевает решение оптимизационной задачи, относительно {P, N}, сводящуюся к минимизации трудовых затрат на измерение и фиксацию таких характеристик:
C(P, N) > min.
Другими словами, необходимо найти такие параметры кадастрового шаблона {P, N}, критерий трудовых затрат на измерение и фиксацию которых на этапе выездных работ был бы минимальным с условием соблюдения порога общей информативности документа Iш.
Ранее была определена необходимость наличия строго соответствия постобработки D(P, N) над шаблоном {P, N} с конечным и полным документом {Pш, Nш}. Составляющая функции постобработки, отчет di, включает и оперирование с исходной матрицей M в зависимости от включенного параметра шаблона pi и смежных с ним наборов характеристик:
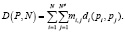
Восстановленные оператором D характеристики обозначим как набор {Pв, Nв}.
Справедливо следующее неравенство-ограничение в поиске {P, N} при решении целевой задачи минимизации: Inf{Pв, Nв} ≥ Inf{Pш, Nш} и {Pш, Nш}∈{Pв, Nв}, при переходе D(P, N) → {Pв, Nв}. Соответствия P∈Pш и D(P, N) ≠ –∞ в таком случае подразумеваются априори.
Формулировка целевой проблемы означает поиск решений комбинаторными методами оптимизации и вариацию размерностью задачи с учетом удовлетворения обозначенного ограничения. Говоря о практической реализации решения, строго аналитические подходы исключены теорией комбинаторики, что подразумевает использование численного моделирования [6].
Поиск методов решения будем осуществлять среди методов решения задач выбора объектов, согласно их общему целевому назначению. Дадим краткие характеристики существующих методов:
– метод полного перебора. Как было сказано ранее, использование этого метода не является эффективным с точки зрения затрат ресурсов вычислений, однако использование его в данной работе примет характер эталонного;
– метод использования сетей Холпфилда или других схожих нейронных сетей. Является менее эффективным в условии нетривиальности входных данных и матрицы критериев;
– жадные алгоритмы. В настоящей работе будут использоваться для формирования промежуточных вычислений оценок;
– метод ветвей и границ. Является наиболее точным и эффективным в условиях рассматриваемой проблематики, так как:
a) не привязан к конкретному виду матрицы отношений;
б) является умеренным перебором, что говорит о его скорости и точности.
Приведем краткое описание такого алгоритма, реализованного программно в модуле нахождения решений задачи оптимизации.
Суть метода состоит в последовательном разделении множества всех возможных решений. Как правило, анализируют такое множество на матрице отношения по включению всех строк и столбцов. В нашем случае, такая матрица есть отношение пар параметров шаблона.
Алгоритм оперирует верхними и нижними оценками, одна из которых определяется «жадным» способом [7]. Далее, верхняя граница и все связанное с ней подмножество отсекается из перебора решений при условии, что она не больше нижней границы, определенной на этапе расчета ранее. Рассмотренные операции на матрице называются ее приведением по столбцам. Глубина приведения отражает меру сокращения множества возможных решений.
В условиях решения задачи максимизации исключение неперспективных строк матриц будет означать замену их на –∞.
Анализ матрицы и дальнейшее сокращение начинают с ее приведения к матрице «тяжелых нулей», что означает элементы, полученные вычитанием из параметров матрицы локальных максимумов, определенных «жадной» выборкой.
В математическом представлении, пусть:
G – множество всех возможных параметров объекта недвижимости;
j(G) – локальная сумма постоянных приведения на исходной матрице М;
M1 – приведенная матрица, полученная вычитанием локальных максимумов и содержащей «тяжелые нули».
Таким образом, множество j(G) составило первый условный шаг работы такого алгоритма.
В матрице M1 устанавливается самый легкий нуль (имеет место максимизация). Пусть его координаты (i, j).
G делим на две условные части:
– множество решений M10, содержащее (i, j) и все решения «сверху» по ребрам графа решений;
– остальное множество M11, в том числе не содержащее такое решение.
Проведем анализ локальных решений M10 и M11 на удовлетворение границам расчета.
При движении найденной информативности шаблона в сторону максимума такое значение набора принимается как часть общего решения и включается в дальнейший анализ приведенной матрицы M2, образованной от указанных изменений. Это решение играет роль верхней границы.
С другой стороны, будет и неперспективное решение, отсекающее все ветви порождающего собой графа.
Нижнюю границу снова сформирует результат «жадного поиска» на матрице M2.
Алгоритм работает до тех пор, пока не будет рассмотрено каждое решение, что делает его точным.
Экономия вычислений за счет исключения ветвей графа G делает такой алгоритм эффективным: неперспективные ветви не рассматриваются и не рассчитываются.
К тому же алгоритм прост в своей программной реализации и универсален к любому виду матриц отношений M.
Результаты исследования и их обсуждение
Как было указано ранее, настоящая задача является комбинаторной, что априори подразумевает существование точного решения оптимизации. Такое решение может быть достигнуто использованием метода полного перебора, однако ввиду довольно низкой скорости его работы и фактически быстрого роста сложности задачи при увеличении размерности, сравнительный анализ результатов придется проводить на сравнительно малых размерностях матрицы отношений целевой задачи.
В ходе математического моделирования, размерность задачи бралась вариациями до 10 параметров описания шаблона. Отметим, что на каждой вариации численное решение методом ветвей и границ точно совпало с полным перебором, что с условием точности метода ветвей и границ характеризует правильность реализации собственного метода и алгоритмов оценки границ.
С другой стороны, очевидна результативность метода ветвей и границ в скорости поиска решения, что наглядно демонстрируется на приведенном графике на рис. 1.
Отметим, что значительное отставание метода полного перебора проявилось уже на размерности матрицы отношений, равной 9, что делает реальным использование такого метода только в оценке точности реализации искомого.
С точки зрения практической реализации найденной методики в вопросе синтеза шаблонов кадастровой информации, пример результата функционирования системы приведен на рис. 2. Обозначенный рисунок демонстрирует адаптивный подход в реализации решения задачи синтеза шаблона паспорта объекта, т.е. на основе данных из БД были выбраны соответствующие объекты и их характеристики, а решение задачи оптимизации характеристик позволило свести к минимуму обозначенные параметры измерений и координат местности.
На основе обозначенных координат на этапе последующего анализа документа будет восстановлен полный кадастровый паспорт объекта. Однако стоит отметить необходимость экспертной оценки полученного документа оператором системы, что говорит о необходимости детальной проработки пользовательского интерфейса системы.
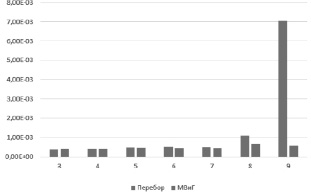
Рис. 1. Сравнительный анализ зависимостей времени поиска решений (мс) методом полного перебора и ветвей и границ от общей размерности задачи
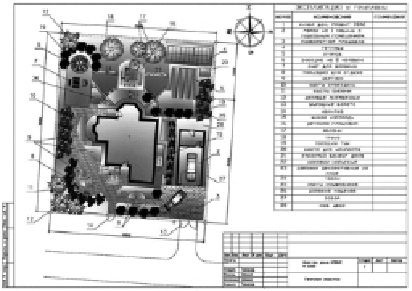
Рис. 2. Пример восстановленного шаблона по знаниям о кадастровом объекте из базы БТИ и оптимизации состава всего набора характеризующих параметров
Выводы
На основе полученных результатов следует сделать вывод об уместности и относительно высокой эффективности использования обозначенного решения в составе алгоритмического обеспечения информационной системы кадастровой инвентаризации и учета.
Библиографическая ссылка
Ишевская В.В., Коробова И.Л., Майстренко Н.В., Евдокимов А.А. ОПТИМИЗАЦИЯ ШАБЛОНОВ ДЛЯ ДАННЫХ ИЗМЕРЕНИЙ В ИНФОРМАЦИОННОЙ СИСТЕМЕ КАДАСТРОВОЙ ИНВЕНТАРИЗАЦИИ И УЧЕТА // Международный журнал прикладных и фундаментальных исследований. 2019. № 8. С. 119-123;URL: https://applied-research.ru/ru/article/view?id=12837 (дата обращения: 08.03.2026).

