Внешний вид любого объекта задают такие его характеристики, как его отражающие и рассеивающие свойства. Вид этих характеристик можно задать с помощью распределения коэффициентов отражения света, падающего на поверхность тела, по интенсивности G(x, y, z) и амплитуде g(x, y, z). Функциональная зависимость для амплитуды имеет вид
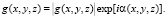(1)
Модуль амплитудной составляющей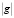 
и ее фазовая составляющая α задают фазовое изменение света, который падает после отражения от произвольной точки (x, y, z) рассматриваемого объекта. Функциональная связь между значениями G и g задается соотношением
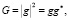(2)
где «*» представляет собой комплексно сопряженные величины.
Для распределения амплитуд и фаз светового поля вдоль поверхности исследуемого объекта можно записать следующее выражение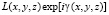 
. Распределение светового поля в этом случае для некоторой рассматриваемой поверхности задается в виде интегрального соотношения Кирхгофа
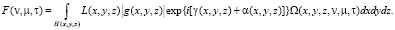
Если выполняется условие
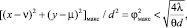(3)
здесь φмакс – наибольшая величина угла, значение его задается в радианах, под которым виден объект с расстояния d, θ – некоторый коэффициент, задающий наибольшую фазовую ошибку, величина которой равна π/θ, то интегральное соотношение Кирхгофа можно преобразовать в интеграл Френеля [1–2]:
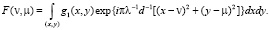(4)
Соотношение (4) можно использовать для синтеза голограмм, которые так и называют – синтезированные голограммы Френеля.
Целью данной работы является рассмотрение процесса синтеза голограмм Френеля.
Дискретное представление голограммы Френеля
Рассмотрим дискретное представление голограммы Френеля:
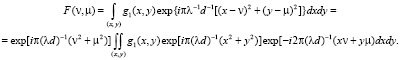(5)
Для ограниченного объекта (–Xмакс, Xмакс; –Yмакс, Yмакс), знание точек отсчета функции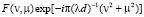 
позволяет полностью ее восстановить методом интерполяции:
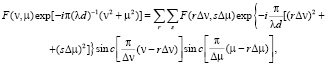(6)
где
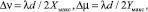
Δξ = λd/2Xмакс, Δη = λd/2Yмакс. (7)
То есть функция F(ν, μ) полностью определена заданными точками отсчета [3–4]:
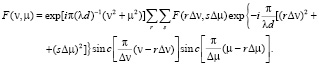(8)
Подбор фазы может быть может быть осуществлен, например, путем освещения голограммы
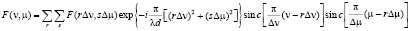(9)
волновым фронтом сферического вида с соответствующим радиусом кривизны
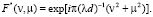(10)
Посмотрим теперь, как найти отсчеты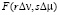 
. Из (5) получаем
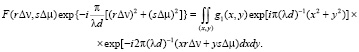(11)
Объект можно описать зависимостью коэффициента отражения по интенсивности от координат точек поверхности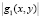 
. Точки дискретизации функции 
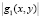позволяют, так как функция достаточно гладкая, полностью ее восстановить методами интерполяции с помощью некоторой функции β(x, y) [5–7]:
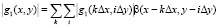, (12)
здесь Δx, Δy – шаги дискретизации вдоль координат x и y .
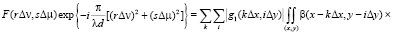
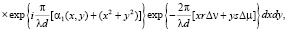(13)
здесь α1(x, y) – функция, пропорциональная фазовой составляющей отражающего коэффициента рассматриваемого объекта.
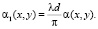(14)
Добавим взаимно уничтожающие друг друга фазовые множители в дискретизированном виде, как под знак суммы, так и под знак интеграла в (13)
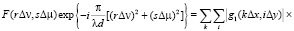
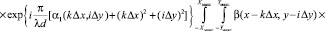
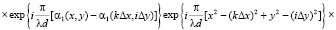
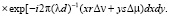(15)
Введем дополнительные условия:
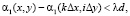
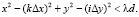(16)
Указанные дополнительные условия показывают, что погрешность в описании профиля объекта и отклонение формы волнового фронта от сферической формы были пренебрежительно малы, и потому можно было записать [8–10]
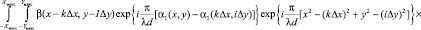
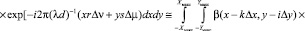
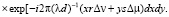(17)
Интегральное соотношение в правой части (17) можно преобразовать следующим образом:
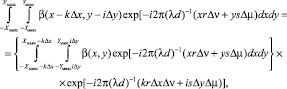(18)
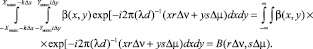(19)
Сделав подстановку (18) и (19) в (15), получаем
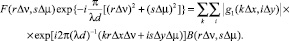(20)
Процесс суммирования по k и i в (20) осуществляется в пределах [–Xмакс/Δx, Xмакс/Δx] и [–Yмакс/Δy, Yмакс/Δy] соответственно.
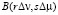можно определить как маскирующую функцию, так как вне пределов некоторого интервала по ν и μ она обращается в нуль. В случае интерполяции объекта в соответствии с теоремой отсчетов
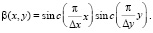(21)
Откуда
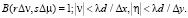(22)
Из (22) можно видеть, что наибольшие значения r и s, для которых вычисляется сумма, задаются соотношениями [11–13]
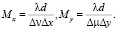(23)
Cогласно (7)
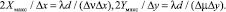(24)
Таким образом, имеем
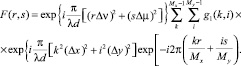(25)
С целью устранения в (25) размерных величин, введем следующие обозначения:
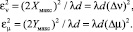(26)
Окончательно получаем
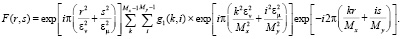(27)
Соотношение (27) описывает дискретное преобразование Фурье. Вычисление такого преобразования требует помимо наличия матрицы g1(k, i), которая определяет распределение амплитуды света вблизи объекта, еще знание величин εν и εμ, которые задаются условиями (26) и характеризуют относительные размеры объекта, наблюдаемого из произвольной точки плоскости регистрации голограммы [14–15].
Как видно из сказанного, расчет синтезированной голограммы Френеля сводится к определению матрицы {F(r, s)} по матрице отсчетов объекта g1(k, i) и аналогового интерполирования полученных точек дискретизации в соответствии с (8)–(10).
Выводы
Трехмерная голография в самом общем случае описывается интегралом Кирхгофа. Расчет такого интеграла аналитически, даже в случае простейших объектов, задача достаточно сложная и чаще всего неразрешимая. Попытки решения интеграла численными методами приводят к алгоритмам, которые требуют огромного объема машинных ресурсов. Поэтому для расчета световых полей в так называемой средней зоне (зона Френеля) трехмерный интеграл Кирхгофа сводят к двумерному интегралу Френеля. В рассмотренной работе предлагается оптимальный метод такого перехода, позволяющий свести к минимуму возникающие при этом погрешности. Кроме того предложена схема дискретизации амплитудных и фазовых составляющих световой волны, что позволяет эффективно осуществлять дискретизацию интеграла Френеля. Также показано, что дискретное преобразование Френеля можно свести к дискретному преобразованию Фурье, что позволяет использовать алгоритмы быстрого преобразования Фурье при расчетах синтезированных голограмм Френеля.
Библиографическая ссылка
Жумалиев К.М., Исманов Ю.Х., Алымкулов С.А. РАСЧЕТ СИНТЕЗИРОВАННОЙ ГОЛОГРАММЫ ФРЕНЕЛЯ // Международный журнал прикладных и фундаментальных исследований. – 2019. – № 8. – С. 130-134;URL: https://applied-research.ru/ru/article/view?id=12839 (дата обращения: 19.04.2024).