Искусственный газлифт (ИГЛ) широко используется для добычи нефти из месторождений, в которых естественный приток из пласта является низким. Эта технология подходит для случаев, когда стоимость газа низкая или имеется газ высокого давления. Принцип ИГЛ основан на растворении подаваемого газа в нефти и снижении гидростатического давления, что увеличивает перепад давления между пластом и нижней частью скважины, в результате чего увеличивется приток нефти из пласта. Недостатком технологии ИГЛ является возможность режима неустойчивого потока нефти в лифтовой (внутренней) трубе, проявляющегося в возникновении колебаний расхода, известного как прерывистый поток. Эти режимы трудно предсказать, поскольку динамика системы достаточно сложна. Разработке динамических моделей ИГЛ посвящен ряд публикаций.
Модель в виде дифференциальных уравнений в частных производных (ДУЧП) можно построить, рассматривая падение давления, вызываемое изменением высоты, трением и ускорением. Модель ИГЛ третьего порядка с сосредоточенными параметрами, учитывающая законы распределения давления по всей длине скважины в затрубном пространстве и лифтовой трубе, была предложена [1]. Кроме того, модель с сосредоточенными параметрами высокого порядка и решение, основанное на ДУЧП, были предложены [2] и [3] соответственно.
Цель исследования: разработка системы моделирования газлифта реального времени. В работе представлен алгоритм полиэтиленовых пакетов в качестве решения для модели ИГЛ, описываемой дифференциальными уравнениями в частных производных (ДУЧП) вместе с с уравнениями состояния нефти и газа. Описано примение этого подхода в системах моделирования газлифта реального времени, используемого в составе аппаратных средств в контуре системы управления ИГЛ, который может быть использован для определения неустойчивых режимов и настройки контроллеров промышленной системы управления.
Динамика искусственного газлифта
В системе искусственного газлифта компрессоры нагнетают газ высокого давления через газовый клапан в затрубное пространство. Оттуда газ поступает через обратный клапан в лифтовую трубу. Закачиваемый газ снижает гидростатическое давление и таким образом увеличивает перепад между давлением пласта и давлением в нижней части скважины. Добываемые флюиды (смесь нефти, газа и, как правило, воды) подаются на сепаратор. В нём флюиды разделяются на нефть, воду и газ. Выделенный на сепараторе газ подается обратно на компрессор, и цикл повторяется снова. Обычно в ИГЛ используется попутный газ из самой скважины, что гарантирует отсутствие нежелательных химических реакций.
Модель, описываемая ДУЧП, учитывает падение давления, вызываемое трением и гравитацией. Возможны эффективные численные решения, построенные на этой модели [2]. Эта модель может обеспечить более точные результаты по сравнению с упрощенной моделью третьего порядка и предоставляет возможность более эффективного численного решения, чем модели, базирующиеся на таких пакетах, как Comsol Multiphysics© и Ansys© [4].
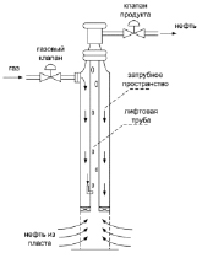
Рис. 1. Схема искусственного газлифта
В лифтовой трубе движение нефтегазовой смеси описывается следующим уравнением:
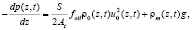 (1)
(1)
где p – давление в лифтовой трубе,
z – вертикальная координата,
u0 – приведенная скорость,
r – плотность нефтегазовой смеси,
g – ускорение свободного падения,
At – площадь сечения лифтной трубы,
f – коэффициент трения,
S – коэффициент, учитывающий размерность.
Формула (1) должна быть дополнена уравнениями состояния для нефти и газа, описывающими их физические свойства. Эти зависимости приведены ниже. Алгоритм, или компьютерная модель, названная алгоритмом полиэтиленовых пакетов, был предложен в работе [2]. Алгоритм полиэтиленовых пакетов реализуется путем синхронной дискретизации дифференциальных уравнений, описывающих динамику газлифта, одновременно по времени и пространственной координате.
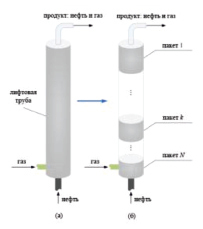
Рис. 2. Схема алгоритма полиэтиленовых пакетов для системы газлифта (для трубопровода): (а) реальный трубопровод, (б) виртуальное разбиение на пакеты
Принцип этого алгоритма состоит в рассмотрении последовательности виртуальных цилиндрических полиэтиленовых пакетов, заключающих в себе нефтегазовую смесь в лифтовой трубе, в соответствии со следующим:
– Флюиды (смесь нефти и газа) рассматриваются как виртуально заключенные в полиэтиленовые пакеты.
– Объём каждого полиэтиленового пакета является переменным и зависит от давления.
– Флюиды равномерно распределены в каждом пакете, но давление в пакете является функцией вертикальной координаты.
– Флюиды не перетекают из одного пакета в другой.
– Пакет формируется в месте подачи газа в лифтовую трубу за счет смешивания нефти и газа в течение заданного интервала времени.
– При достижении пакетом верха лифтовой трубы он опорожняется.
– Давление в верхней части k-го пакета равно давлению в нижней части (k + 1)-го пакета.
Давление и плотность распределения в каждом пакете определяются следующими зависимостями:
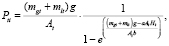 (2)
(2)
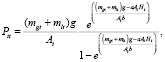 (3)
(3)
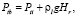 (4)
(4)
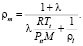 (5)
(5)
В алгоритме полиэтиленовых пакетов, предложенном в работе [2], использовались уравнения идеального газа для описания свойств нефтегазовой смеси, что соответствует физической модели, согласно которой газ содержится в нефти в виде пузырьков. Однако это справедливо только для давления ниже давления точки начала образования пузырьков (кипения).
Использование более точных уравнений состояния нефти и газа значительно повышает точность модели и правильность прогнозирования режимов устойчивого и неустойчивого потока.
Уравнения состояния нефти и газа
Для описания состояния нефтегазовой смеси важно, находится ли рассматриваемое давление ниже или выше так называемого давления точки кипения. Нефтяные скважины эксплуатируются длительное время, и в большинстве случаев давление в лифтовой трубе снижается и достигает значения, меньшего давления точки кипения. При этом начинают формироваться газовые пробки, что приводит к прерывистому потоку [5]. Когда давление в лифтовой трубе меньше давления точки кипения, жидкая фракция нефтегазовой смеси находится в насыщении. Однако если давление в лифтовой трубе начинает расти и становится выше, чем давление точки кипения, то газ содержится в нефти в растворенной форме, что называется режимом недонасыщения. Для точного описания поведения нефтегазовой смеси необходимо определить диапазоны давления, когда реализуется режим насыщения и когда реализуется режим недонасыщения. Одним из наиболее известных и широко используемых уравнений состояния в нефтяной и газовой промышленности является корреляция Васкеса – Беггса [6]. Эта корреляционная зависимость содержит соотношения для определения газового фактора смеси, коэффициента объёмного расширения нефти и сжимаемости нефти. Эта корреляция базируется на более чем 600 лабораторных исследованиях пластовых флюидов, собранных в различных месторождениях. Корреляции делятся на две группы в зависимости от относительного удельного веса нефти: те, что меньше 300 °API, и другие, превышающие 300 °API. Согласно корреляционным зависимостям Васкес – Беггса [6], давление точки кипения равно
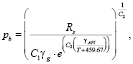 (6)
(6)
где 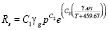 – газовый фактор смеси, стандартный фут3/баррель в стандартных условиях,
– газовый фактор смеси, стандартный фут3/баррель в стандартных условиях,
RS = RSB – растворенный газовый фактор смеси, стандартный фут3/баррель в стандартных условиях (scf/STB) для давления в зоне насыщения,
T – температура, °F,
γg – удельный вес газа (для воздуха γg = 1),
γAPI – плотность нефти, °API,
p – давление, psia.
Сжимаемость нефти определяется отношением степени изменения объема сырой нефти на единицу изменения давления, при постоянной температуре. Как правило, изотермическая сжимаемость может быть описана в виде дифференциального уравнения, на основе следующей формулы:
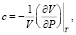 (7)
(7)
где V – обьём флюида,
P – давление флюида,
T – температура флюида.
T обозначает тот факт, что изменение в объеме жидкости происходит только из-за изменения давления при постоянной температуре (изотермическое состояние). Таким образом, для определения иρ) используются уравнения, зависящие от того, находится ли давление в зоне насыщения или недонасыщения. Эти параметры являются функциями давления точки кипения (pB). Для зоны насыщения (ρ ≤ ρB), изотермическая сжимаемость сырой нефти определяется следующим образом:
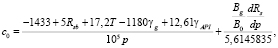
где B0 – объёмный коэффициент для нефти (FVF), определяемый как
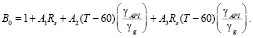
Корреляционные зависимости для газа даны как уравнения состояния реального газа:
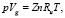 (8)
(8)
где p – абсолютное давление, psia,
Vg – объём газа, м3,
Z – коэффициент сжимаемости газа (коэффициент сжимаемости), безразмерный,
n – число киломолей,
Ru – универсальная газовая постоянная, 18.3145 Дж/Моль•К,
T – абсолютная температура, K.
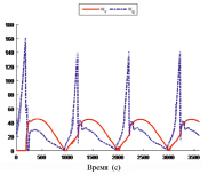
Рис. 3. Массовый расход жидкости в кг/с
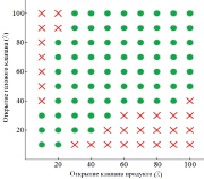
Рис. 4. Диаграмма устойчивости
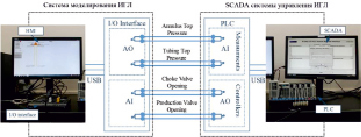
Рис. 5. Система моделирования ИГЛ, подключенная к системе управления, выполненной на ПЛК
Приведенные выше корреляционные зависимости используются в настоящем исследовании в сочетании с алгоритмом полиэтиленовых пакетов. На самом деле, для каждого полиэтиленового пакета используются корреляционные зависимости нефти и газа для описания состояния флюидов. Многочисленные решения уравнений (1)–(8) с использованием алгоритма полиэтиленовых пакетов для различных условий работы показывают, что режимы устойчивого и неустойчивого потока могут быть ясно и точно определены. Пример неустойчивого (прерывистого) потока приведен на рис. 3. Диаграмма, показывающая устойчивые и неустойчивые режимы для различных положений газового клапана и выходного клапана, приводится на рис. 4. Результаты, основанные на алгоритме полиэтиленовых пакетов, совпадают с результатами, полученными с помощью программного обеспечения Dynalift©, в основу которого положены эмпирические данные.
Система моделирования искусственного газлифта
Ввиду высокой эффективности алгоритма полиэтиленовых пакетов стало возможным разработать систему моделирования газлифта реального времени, предназначенную для использования в составе аппаратных средств в контуре системы управления ИГЛ. Система моделирования газлифта может быть использована для тестирования и настройки алгоритмов управления, реализованных на программируемых логических контролерах (ПЛК) или в распределенной системе управления (РСУ). Система моделирования является программно-аппаратным продуктом, который выполнен на высокопроизводительном компьютере (Intel® Xeon®, с 16 GB RAM) и имеет стандартный интерфейс с РСУ или ПЛК (4–20 mA, 0–10 V, HART или сетевой интерфейс). Система моделирования, подсоединенная к системе управления на основе ПЛК, показана на рис. 5. Программное обеспечение, которое помимо модели и алгоритма решения включает в себя интерфейс «Человек – машина» (ИЧМ), написана на языке C#. Выполнение алгоритма синхронизировано с реальным временем, чтобы сделать систему моделирования совместимой с системами управления, реализованными на ПЛК или РСУ. Однако процесс, который она имитирует, достаточно медленный, и при тактовой частоте реализации алгоритма полиэтиленовых пакетов величиной в одну секунду возможно увеличение скорости расчета с применением данного алгоритма до 10 раз по сравнению со скоростью протекания реального процесса. Это позволяет производить тестирование и настройку системы управления гораздо быстрее. Вместе с тем при использовании ускоренного режима настройка контроллеров ПЛК/РСУ происходит при масштабировании постоянных времени. Таким образом, после осуществления настройки эти постоянные времени должны быть увеличены в число раз, соответствующее используемому коэффициенту ускорения моделирования.
Заключение
В статье представлено исследование, включающее разработку математической модели ИГЛ, основанной на эффективных вычислительных методах динамики жидкости и газа, уравнениях состояния нефти и газа и реализации этой модели в программно-аппаратном продукте – системе моделирования АГЛ реального времени. Использование разработанного продукта для идентификации устойчивых и неустойчивых режимов эксплуатации АГЛ, а также настройки контроллеров, выполненных в ПЛК/РСУ, показало его удобство и практическое значение.
Авторы выражают признательность за финансовую поддержку, оказанную проектом PIRC 14506 Петролеум института, Абу-Даби, ОАЭ.
Библиографическая ссылка
Бойко И.М., Аль-Дурра А., Абушавиш И., Матраджи И. МОДЕЛЬ ИСКУССТВЕННОГО ГАЗЛИФТА И ЕЕ РЕАЛИЗАЦИЯ В СИСТЕМЕ МОДЕЛИРОВАНИЯ РЕАЛЬНОГО ВРЕМЕНИ // Международный журнал прикладных и фундаментальных исследований. 2019. № 10-1. С. 154-158;URL: https://applied-research.ru/ru/article/view?id=12884 (дата обращения: 15.12.2025).

