В 1693 г. Э. Галлей, проведя анализ наблюдений лунных затмений, проведенных в отдаленном прошлом и в современную ему эпоху, установил, что средняя скорость орбитального движения Луны постепенно возрастает. Ускорение Луны по расчетам Галлея составило около 10" за столетие. На основании этих данных Галлей сделал вывод о том, что наш спутник постепенно приближается к Земле [1].
Попытки объяснить вековое ускорение Луны через гравитационное влияние со стороны других тел Солнечной системы предпринимались П. Лапласом (1783 г.) и Д. Адамсом (1853 г.). Однако они не привели к успеху. В 1865 г. Ш. Делоне высказал предположение, что причиной аномального движения Луны может являться приливное трение в системе «Земля – Луна». Но в то время не все согласились с такой точкой зрения. В 1885 г. русский астроном Н.П. Долгоруков в своей магистерской диссертации высказал сомнение по поводу того, что приливы могут оказывать хоть сколько-нибудь заметное влияние [1].
В настоящее время приливы продолжают считаться основной причиной наблюдаемого векового ускорения Луны. При этом, согласно приливной теории [2], основная часть эффекта должна приходиться на долю лунных приливов в мелководных морях, а приливами в твердой Земле можно пренебречь. Пренебрегают также и солнечными приливами, так как они существенно меньше лунных приливов по амплитуде и самостоятельно не наблюдаются [2].
Механизм взаимодействия Луны и Земли в приливной теории выглядит следующим образом. Приливная волна, вызванная гравитационным полем Луны, движется навстречу вращению Земли. В мелководных морях эта волна вызывает приливные течения, которые теряют свою энергию за счет трения о дно бассейна. Поскольку сила трения направлена против вращения Земли, скорость ее вращения постепенно уменьшается и земному наблюдателю кажется, что Луна ускоряет свое движение по орбите. При этом Луна, получая дополнительный момент количества движения за счет силы притяжения приливного горба, смещенного относительно линии Земля-Луна, должна постепенно удаляться со скоростью около 3–4 см в год. За счет этого орбитальная скорость Луны должна уменьшаться, а ее положение на орбите будет отставать на 4" за столетие. Однако эффект, вносимый замедляющейся Землей, намного больше, поэтому наблюдателю должно казаться, что Луна движется по орбите с возрастающей скоростью. Таковы основные положения приливной теории, выдвигаемые в связи с наблюдаемым вековым ускорением Луны [1, 2].
Практически, наблюдая с Земли за движением Луны, можно определить лишь суммарную угловую невязку σ в положении Луны, обусловленную как непостоянством скорости вращения Земли, так и непостоянством средней орбитальной скорости Луны.
Величина σ, первую оценку которой сделал Галлей, была уточнена современными астрономами. В 1972 г. астрономы К. Эстервинтер и К. Коэн, используя наблюдения 1912–1968 гг. прохождений через меридиан Луны, Солнца и планет, вычислили, что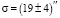 
за столетие. В 1970 г. Р. Ньютон, анализируя древние наблюдения затмений Солнца, получил аналогичный результат σ = 19". По данным Л. Моррисона, полученным в 1973 г. в результате обработки наблюдений долготы Луны за 1955–1972 гг., 
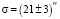. Используя 7000 наблюдений покрытий звезд Луной, Т. Ван Фладерн определил, что 
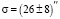. В результате проведения световой локации Луны, с использованием уголковых отражателей, установленных экспедициями «Аполлон-11», «Аполлон-15» и «Луноход-2», было получено σ = 24" [1]. Нужно отметить, что при измерениях σ, выполненных на исторически коротком отрезке времени (порядка 100 лет и менее), возрастает погрешность, обусловленная хаотическими колебаниями скорости вращения Земли [3].
Таким образом, наиболее точные вычисления приводят к значению σ ≈ 20" за столетие. На первый взгляд, величина σ кажется очень маленькой, однако за большое историческое время ей соответствует значительное расхождение в наблюдении солнечных затмений. Оно составляет около 4 часов за 2000 лет. Это позволяет вычислить величину σ при анализе астрономических наблюдений, относящихся к отдаленному прошлому. Наиболее удаленные исторически затмения были описаны Плутархом (–1889 г. и –1931 г.), Гиппархом (–2088 г.) и Архилохом (–2607 г.) [2].
Для объяснения наблюдаемой величины σ с помощью приливной теории, необходимо, чтобы мощность потерь энергии в приливах для всей Земли составляла около 2,7•1019 эрг/сек. Мощность потерь энергии в каждом конкретном случае зависит от скорости приливных течений, глубины моря, а также от состояния дна. Реально все эти факторы трудно оценить, поэтому существуют лишь грубые оценки диссипации энергии в морях. Самые большие потери энергии исследователи отводили Беринговому морю. Например, по оценке Джеффриса мощность потерь энергии здесь составляет 0,75•1019 эрг/сек, а по оценке Хейсканена 0,48•1019 эрг/сек. Однако измерения скорости приливных течений, проведенные в Беринговом море в 1958 г. на первой атомной подводной лодке «Наутилус», показали, что скорости течений здесь завышались в 2–2,5 раз. Приливные течения носят турбулентный характер, поэтому мощность потерь энергии пропорциональна кубу скорости течений. Это означает, что мощность потерь энергии в Беринговом море завышалась приблизительно в 10 раз [2, с. 279]. Сходная ситуация возможна и в других морях.
Если же попытаться объяснить измеренную величину σ за счет приливов в твердой Земле, то для этого необходимо, чтобы угол между линией Земля – Луна и линией, проходящей через диаметрально противоположные приливные горбы, составлял 5 °. Но специальные измерения показали, что этот угол составляет лишь 1 ° [2, с. 287–288].
Изложенное выше дает повод для сомнений в том, что приливы являются основной причиной наблюдаемого замедления вращения Земли. Попытки объяснить наблюдаемое угловое расхождение σ как следствие только приливного трения отчасти были связаны с тем, что не было видно другой физической причины, которая могла бы вызывать потери энергии в системе «Земля – Луна». Однако такая причина существует. В данной статье будет показано, что имеющиеся астрономические наблюдения позволяют построить последовательную неприливную теорию, дающую точное описание наблюдаемого замедления вращения Земли и векового ускорения Луны.
Цель исследования: построение теории, дающей описание наблюдаемого замедления вращения Земли и объясняющей основную причину потерь энергии в системе «Земля – Луна». Предлагаемая теория также предназначена для интерпретации полученных геологами результатов при изучении древних кораллов. Этими исследованиями установлено, что несколько сотен миллионов лет назад число суток в году было существенно больше, чем в настоящее время. Одно из следствий теории позволяет вычислить расстояние от Земли до Солнца в прошлом и выявить причину очень холодного климата на планете в нижнем протерозое и, вероятно, в более раннее геологическое время.
Материалы и методы исследования
Для достижения поставленной цели исследования возникла необходимость обращения к результатам научных работ в смежных с геологией и геофизикой дисциплинах – в астрономии и физике. В качестве исходных данных при построении теории из области астрономии был использован известный эмпирический закон Хаббла. Применение идеи корпускулярно-волнового дуализма из квантовой механики привело к новой интерпретации этого закона. В результате было получено уравнение, описывающее малые потери энергии при вращении и поступательном движении тел, в частности Земли.
Результаты исследования и их обсуждение
В 1929 г. Э. Хаббл, анализируя результаты наблюдений излучения галактик, установил эмпирический закон космологического красного смещения:
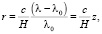(1)
где λ0 – длина волны некоторой спектральной линии в точке испускания фотона, λ – длина волны той же спектральной линии в точке приема излучения, r – расстояние до источника излучения (галактики),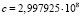 
м/с скорость света, H – постоянная Хаббла [4].
В работе Сэндиджа и Таммана, опубликованной в 1975 г., даются измеренные значения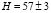 
км/(сек•Мпк) и Н = 55 км/(с•Мпк) для далеких галактик типа Sc. По данным Эйдмана (1969 г.) Н = 51 км/(с•Мпк), а по определениям Вокулера (1970 г.) Н = 50 км/(с•Мпк) [5]. Метод, основанный на наблюдении цефеид был применен при определениях постоянной Н с использованием наблюдений на Космическом телескопе им. Э. Хаббла. Группа ученых под руководством А. Сэндиджа (Институт Карнеги) в 1999 г. получила значение Н = 58 км/(с•Мпк) ±10 % %. Обработка данных наземных измерений красного смещения большого числа галактик и наблюдений сверхновых Ia приводят к постоянной Хаббла 
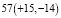км/(с•Мпк) [6]. Одно из самых надежных значений постоянной Хаббла дают наблюдения расширяющихся оболочек сверхновых: Н = 55 км/(с•Мпк) [7, с. 212]. Учитывая эту совокупность данных, в данной статье будет использовано значение Н = 55 км/(с•Мпк) ≈ 1,8•10–18 с–1.
При скоростях движения источника света вдоль луча зрения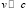 
справедлива формула для известного эффекта Доплера: cz = v. В результате из эмпирического закона (1) можно сделать вывод, что галактики удаляются от наблюдателя со скоростью
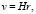(2)
а пространство между галактиками расширяется. Приведенные выше соотношения (1) и (2) лежат в основе космологической теории, предполагающей расширение пространства [4]. Попытаемся на их основе построить теорию, объясняющую наблюдаемые динамические эффекты в системе «Земля – Луна».
Соотношение (2) можно интерпретировать так, что любой линейный элемент пространства увеличивает свою длину со скоростью
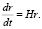(3)
В обычном евклидовом пространстве таким линейным «элементом» может быть, например, длина дебройлевской волны частицы. Согласно экспериментально подтвержденной гипотезе Луи де Бройля, любая частица материи характеризуется длиной волны [8]:
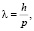(4)
где p – импульс частицы, h – постоянная Планка.
Идея корпускулярно-волнового дуализма материи была высказана Луи де Бройлем в 1924 г. Она явилась обобщением известного тогда только для фотонов соотношения (4) также и на частицы с массой покоя. Это позволило предсказать волновые свойства у электрона, которые были экспериментально обнаружены уже в 1927 г. (К. Дэвиссон и Л. Джермер). Несколько позднее наблюдалась дифракция атомов и молекул (О. Штерн и И. Эстерман), таким образом, было доказано, что соотношение (4) справедливо для любых частиц материи.
Принимая, что в выражении (3) r = λ, получаем уравнение
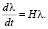(5)
Из соотношений (4) и (5) приходим к уравнению для скорости изменения импульса произвольной частицы, что тождественно действию на нее некоторой силы [9, 10]:
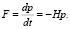(6)
Эта сила направлена вдоль траектории частицы противоположно направлению вектора скорости, что вызывает потери ее энергии.
Таким образом, корпускулярно-волновой дуализм приводит к тому, что при расширении пространства импульсы всех частиц уменьшаются и, напротив, если физический вакуум устроен так, что, взаимодействуя с частицами, уменьшает их импульс, то это будет создавать иллюзию расширения пространства. В соответствии с этим возможны два подхода при объяснении эмпирической закономерности (1). При первом подходе можно считать, что физический вакуум расширяется, а при другом можно исходить из того, что он обладает диссипативными свойствами, определяемыми уравнением (6). В последнем случае постоянная Хаббла приобретает статус универсальной мировой константы. Ниже на примере Солнечной системы мы покажем, что импульсы всех тел, движение которых хорошо изучено, действительно изменяются в соответствии с уравнением (6).
Уравнение (6) фактически означает, что на любую движущуюся частицу или тело с массой m, например планету, действует тормозящая сила [9, 10]:
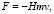(7)
где v – скорость частицы. Рассчитаем вековое ускорение Луны, используя силу (7), действующую на Луну как на точечную массу, а также на любой малый элемент массы вращающейся Земли. Для простоты расчеты будем проводить для круговых орбит. Из-за малого наклонения орбиты Луны к плоскости экватора Земли 5,09 ° будем исходить из приближения, что плоскость орбиты Луны совпадает с плоскостью экватора Земли. Из условия равновесия на круговой орбите орбитальная скорость планеты или спутника
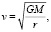(8)
где M – масса центрального тела, r – радиус орбиты,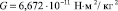 
– гравитационная постоянная. Запишем известное выражение для полной орбитальной энергии спутника с массой m:
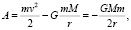(9)
отсюда
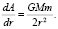(10)
Из выражений (7) и (8) найдем мощность потерь энергии спутником:
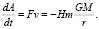(11)
Далее, используя соотношения (10) и (11), получим скорость уменьшения радиуса орбиты:
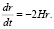(12)
После интегрирования уравнения (12) приходим к формуле, описывающей уменьшение радиуса орбиты во времени:
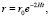(13)
где r0 соответствует величине r в момент начала наблюдения (t = 0). Воспользовавшись третьим законом Кеплера, получаем закон изменения периода обращения
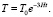(14)
Отсюда следует постепенное возрастание угловой скорости радиус-вектора планеты
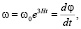(15)
После интегрирования уравнения (15) находим угол, который опишет радиус-вектор за время t:
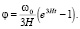(16)
В ньютоновской теории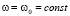 
, соответственно 
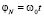. После нахождения угловой невязки 
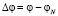и разложения экспоненты в степенной ряд получаем
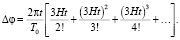(17)
Пренебрегая членами, в которых H имеет показатель степени >1, находим, что радиус-вектор любого спутникового тела за время t будет «убегать» вперед по орбите по отношению к предсказаниям, сделанным на основе теории Ньютона на угол [9, 10]:
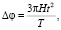(18)
где T – период обращения спутника.
Из уравнения (6) также можно получить закон изменения периода вращения планеты вокруг оси. Для точки, находящейся на расстоянии x0 от оси вращения планеты, линейная скорость вращения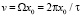 
, где Ω – угловая скорость вращения, τ – период вращения. Поэтому из соотношения (6) следует уравнение для скорости увеличения периода вращения тела
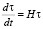(19)
и формула, описывающая возрастание периода вращения со временем:
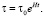(20)
Соответственно, должна уменьшаться угловая скорость вращения тела:
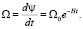(21)
После интегрирования этого уравнения находим угол, который «накручивает» планета за время t:
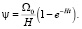(22)
Согласно же предсказанию ньютоновской теории, этот угол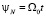 
, соответственно, отставание угла поворота планеты 
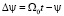. После подстановки в это выражение соотношения (22) и разложения экспоненты в ряд находим:
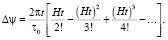(23)
Пренебрегая малыми членами ряда, окончательно получаем [10]:
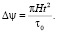(24)
Для Земли период вращения τ0 = 23,9345 часов, и за 100 лет угол, согласно формуле (24), составит 135". При этом отставание по времени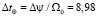 
с, где 
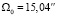с-1 – угловая скорость вращения Земли, а кажущееся вековое ускорение Луны 
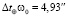, где 
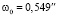с-1 – угловая скорость орбитального движения Луны. Согласно формуле (18), истинное вековое ускорение Луны Δφ = 14,8". В итоге суммарное наблюдаемое с Земли вековое ускорение Луны 
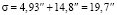[10]. Вычисленная на основе уравнения (6) величина σ хорошо согласуется с приведенными выше данными наблюдений, согласно которым σ ≈ 20" за 100 лет. Полученный результат говорит о том, что существование силы, определяемой выражением (7), полностью объясняет наблюдаемое вековое ускорение Луны, а приливные потери энергии в системе «Земля – Луна», вероятно пренебрежимо малы по сравнению с потерями, появляющимися за счет действия этой силы.
Данные палеонтологии дают нам возможность для независимой проверки соотношений (14) и (20). Установлено, что кораллы каждые сутки наращивают в своей известковой оболочке тонкий известковый слой, толщина которого зависит от длины светового дня. Это позволяет в совокупности суточных слоев выделить годовые слои. Таким образом, кораллы фиксируют число оборотов Земли относительно Солнца за период обращения Земли. При изучении под микроскопом шлифов современных кораллов в годовых слоях обнаруживают 365 суточных поясков. В результате исследований древних кораллов, проведенных Уэллсом, Панеллой и Мак-Клинтоком, охватывающих несколько последних сотен миллионов лет, установлено, что в геологическом прошлом число суток в году было существенно больше и постепенно уменьшалось с приближением к современной эпохе (табл. 1) [2, с. 238].
Отличительной особенностью предлагаемой теории является то, что в ней, согласно (14), период обращения Земли вокруг Солнца меняется с течением времени (уменьшается, приблизительно на 0,54 с за 100 лет). Если в выражении (14) поменять знак времени, то его можно использовать для вычисления T в прошлом:
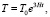(25)
где в случае Земли Т0 = 365,25 суток – период обращения в современную эпоху. Аналогично из формулы (20) период вращения Земли в прошлом:
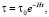(26)
где τ0 = 23,9345 часов – продолжительность суток в настоящее время. Кораллы в строении своей известковой оболочки «запоминают», сколько оборотов вокруг оси совершала Земля относительно Солнца за период обращения по орбите в эпоху роста коралла. Из астрономии известно, как вычисляется период вращения Земли относительно Солнца (солнечные сутки):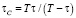 
, где τ и Т соответственно период вращения, и период обращения Земли в рассматриваемую эпоху. Поэтому число солнечных суток N, содержащихся в периоде обращения Земли:
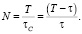(27)
Используя выражения (25), (26) и (27), окончательно получаем
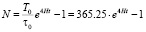сут, (28)
где t – время в прошлое [10].
Результаты вычисления N на основе формулы (28) представлены в последнем столбце табл. 1. Мы видим, что наблюдается хорошее согласие теории с данными палеонтологии. Практически точное совпадение происходит при t = 380 млн лет. Некоторый разброс экспериментальных данных может быть объяснен погрешностью подсчета суточных поясков у кораллов. Таким образом, исследования палеонтологов хорошо подтверждают реальное присутствие силы, определяемой соотношением (7).
Согласно уравнению (12), Луна должна приближаться к Земле со скоростью 4,4 см в год. В то время как теория приливов предсказывает по измеренной величине σ удаление Луны со скоростью 3–4 см в год. По этой же теории Земля должна увеличивать период вращения в темпе (1,5–2) мс/столетие [2]. Однако из уравнения (19) следует, что замедление вращения Земли относительно звезд составляет лишь 0,5 мс за 100 лет. Помимо наблюдений движения Луны, независимые определения темпа замедления вращения Земли были получены на основе измерений склонений (начиная с 1760 г.) и прямых восхождений (с 1835 г.) Солнца, прямых восхождений Венеры (с 1835 г.) и наблюдений прохождений Меркурия по солнечному диску (с 1677 г.). Перечисленные выше наблюдения также дают более низкое значение dτ/dt ≈ 1 мс/столетие [2, с. 237], близкое к тому, что предсказывает уравнение (19). Как уже отмечалось, нужно также учитывать, что при астрономических наблюдениях на сравнительно небольших интервалах времени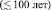 
может оказать некоторое влияние хаотическая составляющая неравномерности вращения Земли [3].
Таблица 1
Число суток в году в геологическом прошлом по данным палеонтологии и согласно теоретическим расчетам
|
Время в прошлое, млн лет |
Число суток в году (N) |
|
|
Данные палеонтологии |
Результаты расчетов по формуле (28) |
|
|
0 |
365 |
365,25 |
|
72 |
370,3 |
371,3 |
|
270 |
384,1 |
388,4 |
|
298 |
387,5 |
390,9 |
|
380 |
398,8 |
398,3 |
|
440 |
407,1 |
403,8 |
Сила, определяемая формулой (7), должна сказываться и на движении планет. За счет ее действия возникает угловая невязка в положении радиус-вектора планеты, которая описывается выражением (18). В результате обработки высокоточных радиолокационных измерений расстояний до планет, проведенных в период с 1960 г. по 1980 г. Институтом радиотехники и электроники АН СССР совместно с рядом других организаций, был выявлен так называемый эффект «запаздывания». Он заключается в том, что при построении теории движения планет на основе ньютоновской теории вычисленное положение планеты на орбите запаздывает по отношению к ее реальному положению [11, с. 31]. Это означает, что планеты движутся по орбите с положительным ускорением – быстрее, чем это следует из ньютоновской теории. Нужно отметить, что согласно Общей теории относительности (ОТО) из-за замедления хода времени в гравитационном поле Солнца, согласно соотношению (33), планеты с точки зрения удаленного наблюдателя должны двигаться медленнее, чем это предсказывает ньютоновская теория. Это может быть учтено путем введения атомного координатного времени, зависящего от гравитационного потенциала Солнца. Обнаруженный эффект «запаздывания» выходит за рамки ОТО. Авторы, открывшие это явление, назвали его новым частным релятивистским эффектом [12]. Путем численного моделирования ими была получена кривая, отражающая изменение измеренного эффекта в зависимости от радиуса орбиты планеты [13].
На рис. 1 представлена теоретическая кривая, полученная для планет Солнечной системы на основе формулы (18). Величина Δφ дана в угловых секундах за столетие (t = 100 лет) при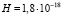 
с-1. Здесь же представлены экспериментальные данные (кружки) для Меркурия (r0 = 0,387 а.е.), Венеры (r0 = 0,723 а.е.), Марса (r0 = 1,524 а.е.) и Юпитера (r0 = 5,203 а.е.), полученные в результате радиолокационных измерений [11, 12].
Из формулы (18) следует, что за 100 лет для Венеры (T0 = 0,61521 лет) Δφ = 1,80", а для Земли (T0 = 1,00004 лет) Δφ = 1,10", т.е. радиус-вектор Венеры опережает радиус-вектор Земли на 0,70" по гелиоцентрической долготе. Из данных, приведенных на рис. 2 в научном сообщении М.Д. Кислика [12, с. 15], следует, что Венера опережает Землю на 0,71", что хорошо согласуется с результатами расчетов по формуле (18).
Приведенные выше результаты расчетов динамических эффектов для Луны, Земли и планет говорят в пользу реального существования силы, которая описывается выражением (7).
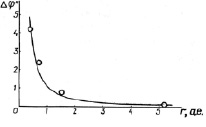
Рис. 1. Уход Δφ радиус-вектора планет по гелиоцентрической долготе по данным радиолокационных наблюдений в угловых секундах за столетие (кружки) для Меркурия, Венеры, Марса и Юпитера [11, 12]. Кривая отражает теоретические значения Δφ, согласно формуле (18)
Попытаемся прояснить физический смысл соотношения (6). В соответствии с формулой (7) описанные выше динамические эффекты в Солнечной системе можно представить как результат действия ускорения, направленного против движения частицы:
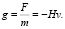(29)
Видно, что это ускорение не зависит от массы частицы. Из всех известных физических полей ускорение, не зависящее от массы пробной частицы, создает только гравитационное поле. Следовательно, сила, определяемая уравнением (6), создается за счет действия некоторого гравитационного поля с напряженностью g = –Hv. Видно, что данное гравитационное поле зависит от скорости частицы. Это означает, что гравитационное поле является индуцированным полем и появляется как результат своеобразной реакции физического вакуума на движение частицы. Поле появляется лишь тогда, когда частица начинает двигаться. Нужно отметить, что в Специальной теории относительности (СТО) движущиеся системы отсчета отличаются от покоящихся систем, в частности, разной скоростью хода времени. При переходе от одной инерциальной системы отсчета к другой видоизменяется и электромагнитное поле. Электрическое или магнитное поле, отсутствующее в одной системе координат, при этом может присутствовать в другой, что отражено в формулах преобразований Лоренца. Соотношение (29) можно представить как некоторое дополнение к СТО. Оно заключается в том, что в системе отсчета, движущейся со скоростью v, появляется гравитационное поле с напряженностью g = –Hv.
Постепенное уменьшение радиуса орбиты Земли (астрономической единицы), которое в соответствии с уравнением (12) должно происходить со скоростью ≈ 1,7 км за 100 лет, косвенно подтверждается данными геологии. Если в соотношениях (13), (14) и (20) поменять знак времени, то можно вычислить, что 4,5 млрд лет назад, в эпоху своего образования, Земля имела радиус орбиты 1,67 а.е., период обращения Т = 2,15 лет и период вращения 18,5 часов. Мощность излучения звезд типа Солнца сохраняется почти постоянной за все время их пребывания (около 10 млрд лет) на главной последовательности эволюционной диаграммы светимость-цвет [14]. Поэтому можно принять, что 45 млрд лет назад полная светимость Солнца была приблизительно равна современному значению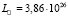 
Вт. Отсюда следует, что плотность потока излучения Солнца 
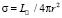в месте расположения орбиты Земли 4,5 млрд лет назад была в 2,79 раз меньше современного значения. Можно предположить, что в это время и несколько позднее планета имела сплошной ледяной покров. Вероятно, как раз об этом свидетельствуют многочисленные следы глобального оледенения, которые обнаружены в отложениях нижнего протерозоя.
Своеобразным индикатором холодного климата в геологии являются специфические горные породы – тиллиты. Они представляют собой неслоистые конгломераты – смеси валунов различного размера с глинами или мергелями, которые по всем признакам являются остатками древних ледниковых морен. Об этом же свидетельствует, например, наличие отполированного и исштрихованного скального ложа, а также такие геоморфологические признаки бывшего присутствия ледников, как долины с плоским дном, цирки и куполовидные выступы, которые имеют гладкий склон с одной стороны (откуда двигался ледник) и шероховатый или зазубренный склон с другой стороны. Наиболее типичные представители нижнепротерозойских тиллитов находятся в свите Гоуганда на юго-востоке Канадского щита. Они имеют возраст 2–2,3 млрд лет и имеют мощность 650–1300 м. На Канадском щите тиллиты такого же возраста находятся вблизи озера Верхнего. Кроме того, они обнаружены в Южной Америке, Индии, Южной Африке, Западной Австралии и в Сарколийской серии Карелии, что указывает на глобальный характер нижнепротерозойского оледенения [15], которое иногда называют Величайшим Оледенением. Согласно расчетам ученых, толщина ледяного панциря планеты в этот период достигала 0,5 км. В архее небольшие открытые водоемы, вероятно, существовали лишь в зонах выделения эндогенного тепла, например вблизи вулканов и в мелководных частях рифтовых зон. В пределах этих водоемов могли существовать первые бактерии фотосинтетики (цианобактерии), которые выделяли относительно небольшое количество кислорода, шедшего в основном на окисление минералов. Вблизи границы архея и протерозоя около 2,3–2,4 млрд лет назад, согласно открытиям геологов, в атмосфере Земли впервые появился свободный кислород. Накопление кислорода происходило настолько быстро, что иногда это событие называют Кислородной катастрофой. Быстрое накопление в атмосфере кислорода можно связать с началом таяния ледяного покрова планеты и с массовым размножением цианобактерий в образовавшихся обширных пространствах открытой воды.
Планета, изначально образовавшаяся за пределами обитаемой зоны (зоны Златовласки), постепенно теряя орбитальную энергию и уменьшая радиус орбиты, в соответствии с формулой (13), постепенно входит в зону обитания и вода на планете переходит из твердой фазы в жидкую фазу. Это увеличивает вероятность появления и последующей эволюции жизни на планете. Существуют некоторые оценки верхней границы обитаемой зоны в Солнечной системе: 1,24 а.е. (Dole, 1964 г.); 1,30 а.е. (Fogg, 1992 г.); 1,37 а.е. (Kasting et al., 1993 г.). На этом фоне несколько заниженной выглядит оценка 1,01 а.е. (Hart et al., 1978 г., 1979 г.). Эти оценки в целом согласуются с расчетами, сделанными на основе соотношения (13), согласно которым во время окончания Величайшего Оледенения 2–2,3 млрд назад Земля находилась на расстоянии соответственно 1,26–1,30 а.е. от Солнца. Таким образом, существование в истории нашей планеты такого геологической эпохи, как Величайшее Оледенение, косвенно подтверждает наличие миграции спутниковых тел к центральному телу, в соответствии с выражением (13), которое получено на основе уравнения (6).
Покажем, что представление о существовании гравитационного поля, которое описывается соотношением (29) не вступает в противоречие с наблюдениями в космологии.
Для изменения энергии фотона, движущегося в пространстве, формально можно записать
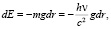(30)
где g – напряженность гравитационного поля, действующего на фотон, v – частота фотона. Воспользовавшись известным соотношением для фотона E = pc, из уравнения (6) найдем мощность потерь энергии фотоном при его «покраснении»:
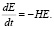(31)
Поскольку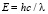 
, то после замены 
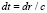уравнение (31) преобразуется к другому виду [9]:
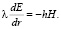(32)
Отсюда видно, что потери энергии E фотоном на длине волны λ составляют по кванту hH.
Из уравнений (30) и (32) находим, что на движущийся фотон действует гравитационное поле с напряженностью g = –Hc, т.е. имеет место частный случай соотношения (29) при v = c. Это позволяет рассматривать космологическое красное смещение как гравитационное красное смещение частоты фотонов, что является новым взглядом на природу этого явления. В свою очередь, это дает возможность независимым способом вычислить наблюдающийся в космологии эффект замедления времени.
А. Эйнштейном теоретическим путем было установлено явление замедления хода времени в гравитационном поле. Действие гравитационного поля описывается выражением [16, с. 110]:
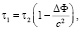(33)
где τ1 и τ2 – длина временных интервалов в двух системах отсчета, ΔФ – разность ньютоновских гравитационных потенциалов между двумя рассматриваемыми точками в этих системах отсчета. Эту взаимосвязь между временными интервалами Эйнштейн получил, анализируя распространение света в системе отсчета, движущейся с постоянным ускорением a. В конечной формуле при переходе к однородному гравитационному полю, в соответствии с принципом эквивалентности гравитационного поля и ускорения, была проведена замена: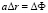 
, где Δr – расстояние пройденное светом. Выражение (33) имеет ограничение на его применимость вблизи массивных тел при значительной кривизне пространства. Оно вытекает из связи кинетической энергии падающей массы m с гравитационным потенциалом. Поскольку ньютоновский предел соответствует скоростям падения 
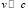, то отсюда принято ограничение на область применения соотношения (33): 
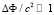. По данным современных наблюдений Вселенная имеет плоскую евклидову геометрию, т.е. представляет собой пространство с нулевой кривизной [17]. Это практически необъяснимо в рамках теории расширяющейся Вселенной [18]. Наличие плоской геометрии пространства тождественно отсутствию крупномасштабного гравитационного поля, что возможно при ограниченном радиусе гравитационного взаимодействия. Рассматривая движение отдельных фотонов, мы будем исходить из того, что они движутся в плоском и нерасширяющемся пространстве, не накладывая при этом ограничения на расстояния.
Индуцированное гравитационное поле g = –Hc приводит к тому, что для наблюдателя, регистрирующего фотон, все будет выглядеть так, как если бы фотон прошел через разность гравитационных потенциалов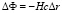 
, где Δr – расстояние от наблюдателя до источника света. При этом в соответствии с соотношением (33), временные интервалы τ1 и τ2 в точке приема и в точке испускания фотона будут связаны соотношением
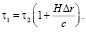(34)
После подстановки в уравнение (5)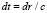 
получаем
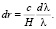(35)
Из этого уравнения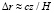 
и соотношение (34) преобразуется к виду
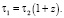(36)
Из формулы (36) для больших расстояний при z = 1 получаем τ1 = 2τ2, т.е. если продолжительность свечения близкого объекта составляет 20 суток, то при z = 1 продолжительность свечения такого же объекта будет равна 40 суток. Это подтверждается наблюдениями кривых яркости далеких сверхновых, которые увеличивают свою ширину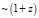 
[19]. В существующей космологической теории, использующей представление о расширении пространства, явление уширения кривых яркости объясняют тем, что за счет расширения пространства фотоны, испущенные в конце вспышки сверхновой, проходят гораздо больший путь, чем фотоны, испущенные в начале вспышки.
Для гравитационного красного смещения частоты фотонов в поле массивных тел справедлива известная формула [20]:
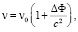(37)
где v0 – частота фотона в точке испускания. В нашем случае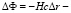 
потенциалов индуцированного гравитационного поля. Поэтому космологическое красное смещение:
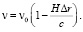(38)
Поскольку v = c/λ, то нетрудно видеть, что из соотношения (38) следует формула (1) закона Хаббла, которую он получил эмпирическим путем для сравнительно небольших расстояний при z ≤ 0,004.
Чтобы получить предполагаемый закон космологических расстояний для больших значений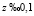 
, проинтегрируем уравнение (35), в результате получим [9]:
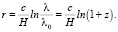(39)
Поскольку для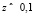 
имеет место известное соотношение 
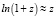, то из формулы (39) при небольших значениях z также следует закон Хаббла, который описывается выражением (1). Из соотношений (34) и (39) следует связь между двумя временными интервалами:
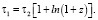(40)
Так как энергия фотона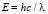 
, то из выражений (39) можно найти, что при движении в пространстве энергия каждого фотона уменьшается 
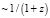. Кроме того, в соответствии с формулой (36), длина временного интервала увеличивается 
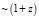или, точнее, согласно выражению (40), 
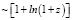. В первом случае регистрируемая болометрическая плотность потока излучения l от любого источника с мощностью излучения L:
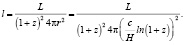(41)
Это выражение похоже на то, которое получается, когда исходят из представления о расширении пространства [21]:
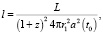(42)
где r1 – радиальная координата Земли при отсчете от светящегося объекта, а(t0) – безразмерный масштабный множитель, который зависит от параметров конкретной выбранной модели.
Считается, что сверхновые типа Ia хорошо подходят на роль стандартного источника света при проверке космологических теорий, так как характеризуются сравнительно небольшим разбросом пиковой мощности излучения и их абсолютная звездная величина в максимуме в среднем составляет –19,2 [21]. Исследовательская группа Supernova Cosmology Project сопоставила результаты наблюдений яркости сверхновых типа Ia с теоретическими значениями (рис. 2) [22]. Сравнения проводились для случая плоской Вселенной, когда между безразмерными параметрами плотности вакуума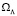 
и плотности нерелятивистской материи ΩM имеется связь 
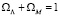. Из данных по сверхновым следует значение ΩM = 0,28 и, соответственно, 
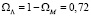. Известное соотношение [21]
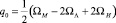(43)
при плотности излучения ΩИ = 0 приводит к отрицательному значению параметра замедления q0 = –0,58, из чего был сделан вывод о том, что расширение Вселенной ускоряется.
Во второй строке табл. 2 приведены теоретические значения звездных величин mB1, полученные автором на основе формулы (41) при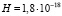 
с-1. Величина 
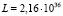Вт была подобрана так, чтобы при z = 0,01 наблюдалось совпадение с кривыми на рис. 2. Данные в третьей строке (mB2) соответствуют модификации выражения (41) для случая замедления времени 
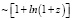. Данные из табл. 2 соответствуют кривым, проходящим через центральную часть облака точек для далеких сверхновых на рис. 2. Поэтому можно считать, что предложенное автором соотношение (41) хорошо соответствует наблюдениям в космологии. При этом не использовалось представление о расширении Вселенной при другом способе описания, основанном на применении уравнения (6).
Таблица 2
Теоретические значения звездных величин сверхновых при разных красных смещениях z
|
z |
0,01 |
0,02 |
0,05 |
0,1 |
0,2 |
0,5 |
1,0 |
|
mB1 |
14,0 |
15,5 |
17,5 |
19,1 |
20,7 |
22,9 |
24,7 |
|
mB2 |
14,0 |
15,5 |
17,5 |
19,1 |
20,7 |
22,8 |
24,5 |
Соотношение (6) позволяет вычислить и температуру космического микроволнового фона, открытого в 1965 г. А. Пензиасом и Р. Вилсоном [4]. Для этого постулируем Вселенную, средние свойства которой не меняются в пространстве и во времени. Такая Вселенная, в частности, должна «уметь» регенерировать запасы водорода, являющегося топливом для звезд. Если бы фотоны не уменьшали свой импульс и энергию в соответствии с уравнениями (6) и (31), то температура Вселенной постепенно поднялась бы до поверхностной температуры нормальных звезд ≈ 6000 К. Однако фотоны постепенно «краснеют» за счет действия индуцированного гравитационного поля g = –Hc и устанавливается более низкая равновесная температура. При этом физический вакуум выступает в роли своеобразного «холодильника», забирая энергию у фотонов. Световое излучение галактик в основном формируется за счет звезд, похожих на Солнце. Оно имеет мощность излучения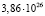 
Вт при массе 
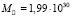кг, т.е. удельная мощность излучения 
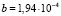Вт/кг. Если среднюю (равномерно распределенную по всему пространству) плотность светящегося вещества галактик обозначить как ρG, то мощность излучения выходящего из единицы объема Вселенной
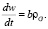(44)
Объемная плотность энергии фотонного газа w = nE, где n – концентрация фотонов. Для простоты можно принять, что все фотоны имеют одинаковую энергию, поскольку это не влияет на конечный результат. Тогда из уравнения (31) мощность уменьшения энергии излучения в единице объема
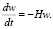(45)
При равновесии должно иметь место равенство
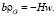(46)
Из него находим объемную плотность энергии
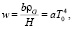(47)
где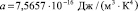 
– постоянная излучения. Отсюда получаем выражение для равновесной температуры Вселенной:
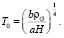(48)
Средняя плотность светящегося вещества Вселенной по существующим оценкам составляет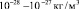 
[4, с. 514], т.е. можно принять 
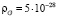кг/м3. В результате из формулы (48) получаем равновесную температуру Вселенной Т0 = 2,91 К, что близко к измеренному значению 2,73 К. Некоторое расхождение можно объяснить неточностью знания параметров ρG и H. По мнению автора, микроволновое фоновое излучение является следствием того, что Вселенная имеет температуру Т0 и потому излучает практически как абсолютно черное тело с такой температурой. В этом случае микроволновый фон не является реликтом горячей стадии Вселенной, которая, как предполагается, образовалась в результате некоторого гипотетического события – Большого взрыва.
По-видимому, нельзя считать, что спектр микроволнового излучения является спектром звезд, испытавшим космологическое красное смещение. Известно, что излучение звезд, похожих на Солнце, в первом приближении является чернотельным. Можно оценить характерное расстояние, которое должен был бы преодолеть свет звезд для увеличения его длины волны до длины волны фотонов микроволнового фона. Пусть в выражении (39)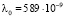 
м, что приблизительно соответствует желтому цвету звезд. Из наблюдений следует, что средняя по спектру энергия квантов микроволнового фона 
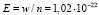Дж. Это соответствует средней наблюдаемой длине волны 
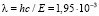м. В результате из формулы (39) получаем 
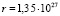м = 143 млрд св. лет. Это приблизительно в 15 раз превышает расстояния, доступные современным телескопам. Маловероятно, что при таких расстояниях Вселенная является прозрачной и свет звезд напрямую доходит до нас с таких больших расстояний. Источником микроволнового излучения, в частности, может быть пыль, присутствующая в небольших количествах в пространстве между галактиками и нагретая до температуры Т0.
Из постоянного существования равновесия, определяемого соотношением (46), между энергией испущенной звездами и энергией поглощенной физическим вакуумом следует, что в межгалактической среде непрерывно образуется новый водород, компенсирующий его потери в ходе термоядерных реакций в звездах. Водородные облака в межгалактическом пространстве действительно существуют. Они обнаруживают себя по абсорбционным линиям поглощения. Это, так называемый Лайман-альфа лес (Lyα – лес). Причиной появления Lyα – леса являются облака нейтрального водорода, расположенные на пути распространения света от объектов, находящихся на космологически больших расстояниях. Линия Лайман-альфа водорода в лабораторных условиях имеет длину волны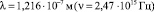 
, что соответствует ультрафиолетовой области спектра. Для облаков, находящихся на разных космологических расстояниях, эта линия имеет разное красное смещение z, что и приводит к появлению «леса» из линий поглощения. Для некоторых далеких источников света этот эффект бывает настолько сильным, что приводит к спаду регистрируемого излучения в соответствующем интервале частот (желоб Ганна – Петерсона (Gunn – Peterson)).
Можно предположить, что из энергии, полученной физическим вакуумом при взаимодействии с излучением, в соответствии с уравнением (31), впоследствии, в результате флуктуаций плотности энергии вакуума происходит рождение частиц, в частности, протонов и электронов, образующих затем водород. Согласно квантовой теории поля в физическом вакууме непрерывно происходят процессы рождения и уничтожения виртуальных квантов физических полей и виртуальных пар частиц, например, электронов и позитронов, а также протонов и антипротонов. Время жизни Δt виртуальной частицы с энергией ΔE определяется принципом неопределенности для энергии и равно h/ΔE. Для того чтобы виртуальные частицы превратились в реальные частицы, им нужно передать энергию больше или равную энергии покоя частицы m0c2, где m0 – масса покоя частицы [23]. Эту энергию они могут получить в области большой по амплитуде флуктуации плотности энергии физического вакуума и за счет флуктуаций кривизны пространства-времени. Считается, что при квантовых флуктуациях кривизны пространства-времени могут образовываться виртуальные черные дыры. Разрыв пары из частицы и античастицы и их превращение в реальные частицы может происходить вблизи горизонта событий виртуальной черной дыры. Одна из частиц падает в дыру, а другая улетает в бесконечность (процесс Хокинга). Таким образом, физический вакуум способен порождать частицы и античастицы. В 1964 г. в экспериментах с каонами впервые экспериментально обнаружено нарушение CP-симметрии (Джеймс Кронин и Вал Фитч). В силу существования этого явления смесь равных количеств вещества и антивещества должна аннигилировать не полностью. В результате останется небольшое количество обычного вещества. Нужно также отметить, что в областях флуктуаций происходит уменьшение энтропии [24, с. 198], в то время как процессы в звездах ведут к возрастанию энтропии. Возможно, что эти противоположно направленные изменения энтропии во Вселенной уравновешивают друг друга.
Представление об одноактном образовании всего вещества Вселенной из одной «точки» лежит в основе известной теории Большого взрыва. В отличие от этого, автор статьи, в сущности, предполагает непрерывное образование некоторого количества частиц во множестве отдельных вакуумных точек. Таким образом, Большой взрыв заменяется большим количеством микроскопических «взрывов», которые происходили как в прошлом, так и продолжают происходить в настоящее время. При этом не происходит расширение пространства. Нужно отметить, что представление о расширении пространства в теории Большого взрыва порождает пока не решенную проблему космологической сингулярности. Предполагается, что в начальный момент Большого взрыва вся материя Вселенной была сосредоточена в «точке» и имела бесконечно большую плотность и бесконечно большую температуру. Однако выяснилось, что при бесконечно большой плотности мера хаоса (энтропия) стремится к нулю, что несовместимо с бесконечно большой температурой. Это создает одну из проблем в теории Большого взрыва.
Водород, образованный в физическом вакууме, впоследствии может идти на образование новых галактик, а также на пополнение запаса водорода в уже существующих галактиках. Группа астрономов из Института астрономии общества Макса Планка (нем. Das Max-Planck-Institut fur Astronomie, MPIA) под руководством Мелиссы Несс (Melissa Ness) создала подробную карту распределения звезд в Галактике по их возрастам. На карте ближе к центру Галактики расположены старые звезды, а на периферии сосредоточены молодые звезды. Кроме того, исследования, проведенные с помощью рентгеновской обсерватории «Чандра», показали, что в центральной части Галактики находится большое скопление нейтронных звезд и, возможно, черных дыр. Этот «рой» из звезд, представленный более 10 тысячами рентгеновских источников, был образно назван «кладбищем» старых звезд, которые по неизвестным причинам мигрировали в центр Галактики [25]. По мнению автора статьи, эти факты можно объяснить тем, что одновременно с поступлением водорода идет процесс сжатия галактики. Так, из соотношения (13) следует, что за время t = 1/2 H = 8,8 млрд лет радиусы орбит звезд уменьшаются в e ≈ 2,72 раз, т.е. вращающиеся галактики устроены по принципу конвейера. Приближаясь к центру крупной галактики, звезды постепенно стареют и в конечном итоге падают в находящуюся в ее центре сверхмассивную черную дыру. Подобные дыры уже обнаружены в центре многих галактик, в том числе и в центре нашей Галактики. Таким путем происходит уничтожение старых звезд, которые уже выработали свое термоядерное топливо. В те эпохи, когда поток падающих в дыру звезд становится особенно плотным, происходит наибольшее выделение энергии. По-видимому, это и порождает эффект квазара [10, 26]. Черные дыры в центрах галактик иногда выбрасывают мощные релятивистские струи вещества (джеты) в двух диаметрально противоположных направлениях, предположительно, вдоль оси вращения дыры. Джеты состоят из протонов и электронов и тем самым они восполняют запасы водорода в межгалактической среде. Механизм ускорения и нагрева плазмы в джетах пока неизвестен. Неизвестно и то, откуда вырываются струи плазмы – из черной дыры или из пространства вблизи нее. Сами черные дыры, в соответствии с теорией Хокинга, постепенно испаряются, излучая преимущественно фотоны, а также частицы с массой покоя и их античастицы. Поэтому есть основания предполагать, что вещество и излучение, падающие в черную дыру, в конечном итоге оказываются в межгалактической среде.
Можно привести дополнительные доказательства того, что в потоке частиц материи действительно образуется гравитационное поле, в соответствии с соотношением (29). В частности, в потоке фотонов его напряженность должна быть равна –Hc. Фотонное излучение Солнца будет приводить к появлению в его окрестности дополнительного гравитационного поля с напряженностью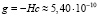 
м/с2 (при 
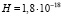с-1), направленного к Солнцу. Космические аппараты «Pioneer-10» и «Pioneer-11» с выключенными двигателями удаляются от Солнца и хорошо подходят на роль пробных масс при изучении малых гравитационных эффектов. Анализ радиосигналов, поступающих с этих аппаратов, при использовании эффекта Доплера позволил измерять их скорость с точностью около 0,1 мм/сек. Оказалось, что после учета всех малых влияний остается некоторый избыточный доплеровский сдвиг частот, который можно интерпретировать как наличие некоторого добавочного ускорения, направленного к Солнцу. Это ускорение для «Pioneer-10», по разным оценкам, составило 
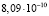м/с2 и 
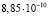м/с2, а в случае «Pioneer-11» 
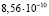м/с2. Аналогично, для космических аппаратов «Ulysses» и «Galileo» были вычислены избыточные ускорения, соответственно, 
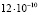м/с2 и 
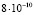м/с2 [27]. В двух последних случаях на борту имелись работающие малые реактивные двигатели системы ориентации. Видно, что космические станции действительно испытывают дополнительное ускорение ≈Hc, направленное в сторону источника фотонов.
Фотонное излучение яркого ядра галактики также должно приводить к тому, что в окрестности ядра будет генерироваться направленное радиально гравитационное поле g = –Hc. С учетом этого, для обращающихся вокруг ядра звезд можно записать условие равновесия на круговой орбите с радиусом r:
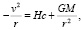(49)
где M – масса ядра, v – скорость движения звезды по орбите. Второе слагаемое, представляющее собой ньютоновскую составляющую ускорения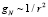 
, быстро спадает при удалении от ядра. Начиная с некоторого радиуса, имеем 
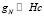, и обращение звезд уже происходит практически только под действием ускорения Hc с орбитальной скоростью
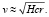(50)
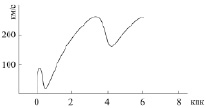
Рис. 3. Зависимость скорости обращения звезд в галактике NGC 7331 от радиуса их орбиты [28]
Это соотношение описывает неньютоновское «твердотельное» вращение крупных галактик, объяснение которому не было найдено. Проблема обозначилась в связи с тем, что орбитальная скорость звезд при их движении в гравитационном поле ядра галактики должна уменьшаться по закону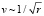 
. Однако на практике наблюдается возрастание скорости звезд с ростом радиуса их орбиты. Можно показать, что ньютоновское гравитационное поле в средней части крупной галактики действительно может быть мало по сравнению с полем g = –Hc. Масса звезд в нашей Галактике равна около 
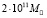при ее радиусе 50000 св. лет, где 
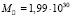кг – масса Солнца. При этом масса ядра (галактического центра) равна 
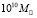. При такой массе ядра и расстоянии от центра Галактики r = 25000 св. лет напряженность ньютоновского поля 
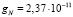м/с2. Видно, что в данном случае 
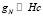, поэтому орбитальная скорость звезд будет описываться приближенно формулой (50) и более точно соотношением (49). Одного ньютоновского поля явно недостаточно для объяснения наблюдаемой в Галактике скорости звезд ≈ 240 км/с, которая приближенно оценена по скорости ближайших звезд относительно Солнца.
В подтверждение вышесказанному вычислим постоянную Хаббла, воспользовавшись следующей из соотношения (50) формулой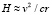 
и графиком измеренной орбитальной скорости звезд в галактике NGC 7331 (рис. 3) [28]. Это крупная спиральная галактика с ярким ядром, которую иногда называют близнецом нашей Галактики. На рис. 3 видно, что начиная с расстояния 0,55 кпк от центра ядра происходит плавный подъем орбитальной скорости звезд, который наблюдается до 3,3 кпк. Скорость обращения звезд в ядре, согласно графику на рис. 3, при r = 0,2 кпк равна 90 км/с, что соответствует массе ядра 
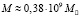. При использовании эффекта Доплера точность измерения скорости вращения галактики повышается с ростом скорости. Поэтому для вычислений целесообразно использовать «твердотельный» участок кривой вращения, соответствующий наибольшим радиусам орбит звезд. Из рис. 3 видно, что при r = 2 кпк и r = 3 кпк орбитальная скорость звезд в галактике равна, соответственно, 190 км/сек и 250 км/сек. Из формулы получаем два значения постоянной Хаббла 
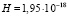с-1 и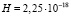 
с-1. При учете массы ядра из соотношения (49) находим немного отличающиеся оценки 
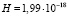с-1 и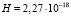 
с-1. Мы видим, что в обоих случаях получаются приблизительно правильные величины постоянной H. Выражения (49) и (50) могут быть использованы для определения постоянной Хаббла в тех случаях, когда расстояние до галактики известно с хорошей точностью, например в результате применения метода цефеид, так как на практике измеряются угловые размеры орбит звезд. Кроме того, галактика должна быть достаточно разреженной, что позволяет пренебречь тяготением звезд за пределами ядра. Благодаря существованию в световом потоке гравитационного поля g = –Hc галактика может более эффективно притягивать к себе водород из межгалактической среды.
Аномально высокую скорость звезд внутри и на периферии галактик при «твердотельном» вращении иногда объясняют существованием гипотетической невидимой («темной») материи, создающей дополнительное гравитационное поле. Существование внутри и за пределами галактик гравитационного поля с напряженностью Hc может полностью или частично снять необходимость привлечения гипотезы о существовании темной материи, в том числе и в скоплениях галактик типа Комы. Если фотон пересекает пучок фотонов, то он должен отклоняться в сторону источника света. Вероятно, это также может создавать эффект присутствия темной материи при наблюдениях прохождения света вблизи светящихся объектов.
Заключение
Переход от изменяющейся длины дебройлевской волны физических объектов к их изменяющимся импульсам, в соответствии с уравнениями (5) и (6), применительно к геофизике, астрономии и космологии приводит к предсказанию новых эффектов, согласующихся с уже имеющимися наблюдениями.
Наблюдаемое ускорение «Пионеров» и «твердотельное» вращение галактик подтверждают реальное присутствие гравитационного поля g = –Hv в потоке частиц, в данном случае фотонов. Существование данного поля вытекает из уравнения (6), поэтому наличие этих эффектов является дополнительным подтверждением правильности сделанных в статье выводов о том, что основная причина замедления вращения Земли и векового ускорения Луны и планет является результатом действия гравитационного поля, предсказанного соотношением (29). Предложенная теория дает объяснение полученному палеонтологами результату, согласно которому число суток в году в геологическом прошлом было существенно больше, чем в настоящее время (формула (28)). Из формулы (13) следует, что 2–2,3 млрд лет назад наша планета находилась на расстоянии, соответственно, 1,26–1,30 а.е. от Солнца. Это согласуется с выводами геологов о холодном климате в нижнем протерозое во время окончания Величайшего Оледенения. Вычисленное расстояние от Земли до Солнца в ту геологическую эпоху практически совпадает с имеющимися оценками верхней границы зоны обитания в Солнечной системе. Эта граница соответствует таким климатическим условиям на планете, когда вода переходит в жидкое состояние. Постепенное приближение Луны к Земле, в соответствии с формулой (13), подтверждается вычислением ее векового ускорения, согласующегося с данными наблюдений. Это может говорить о том, что Луна сформировалась не вблизи Земли, а была захвачена нашей планетой на эллиптическую орбиту, например, после ее столкновения с достаточно крупным спутником Земли.
Полученные в работе результаты показывают, что более тщательные измерения потерь энергии в приливах, возможно, дадут дополнительные основания для пересмотра основной причины наблюдаемого замедления вращения Земли и векового ускорения Луны. Для этого необходимо спланировать и реализовать специальную программу исследований с использованием современных технологий.
Библиографическая ссылка
Рыбкин В.В. ТЕОРИЯ ЗАМЕДЛЕНИЯ ВРАЩЕНИЯ ЗЕМЛИ НА ОСНОВЕ ДАННЫХ ГЕОЛОГИИ, ГЕОФИЗИКИ И АСТРОНОМИИ // Международный журнал прикладных и фундаментальных исследований. – 2019. – № 11. – С. 110-125;URL: https://applied-research.ru/ru/article/view?id=12942 (дата обращения: 21.11.2024).