Известно, что проблемным вопросом при автоматизации технологических процессов при механической обработке изделий является ее автоматизация, предусматривающая разработку не только принципиальной схемы управления, но и математической модели всей системы, позволяющей исследовать динамические процессы при ее работе, а также произвести расчет параметров основных элементов, необходимых для обеспечения ее качественной работы.
Из теории автоматического управления известно, что система регулирования становится неустойчивой при большом значении коэффициента усиления регулятора или при увеличении инерционности регулятора. В дифференциальных уравнениях первого и второго порядка можно утверждать, что система будет устойчивой при всех положительных коэффициентах у переменных в левой части уравнения при любых значениях Т, Крег [1–4]. Автоматическая система регулирования подачи инструмента гидросуппортом будет третьего порядка в трех случаях:
1) математические модели объекта описываются дифференциальным уравнением первого порядка, а регулятора расхода второго порядка;
2) динамика описывается дифференциальным уравнением второго порядка, а регулятор – дифференциальным уравнением первого порядка;
3) дифференциальное уравнение объекта третьего порядка, а регулятор является безынерционным.
Уравнение динамики объекта гидросуппорта описывается дифференциальным уравнением первого порядка:
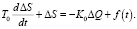(1)
Уравнение динамики регулятора расхода представляется дифференциальным уравнением второго порядка:
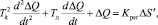(2)
где Тk – постоянная времени, способствующая колебательному переходному процессу; Тд – постоянная времени, способствующая демпфированию колебаний в переходном режиме.
Вывод уравнения регулятора расхода (2) будет сделан при составлении его математической модели.
Для получения дифференциального уравнения системы регулирования необходимо уравнения (1) и (2) решить совместно.
Из уравнения (1) имеем
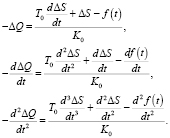(3)
Эти полученные значения подставим в уравнение (2) и после соответствующих преобразований получим уравнение, описывающее динамические процессы всей системы регулирования.
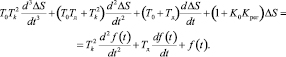(4)
Если автоматическая система регулирования испытывает постоянное возмущающее воздействие, то есть f(t) = const, то уравнение (4) примет вид
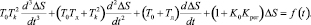(5)
Составим его характеристическое уравнение.
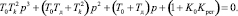(6)
Это алгебраическое уравнение третьей системы имеет три корня.
Рассмотрим три варианта при положительных значениях коэффициентов у переменных в левой части уравнения:
1. Все три корня являются вещественными и отрицательными, то есть
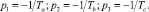(7)
2. Один корень вещественный и отрицательный, а два комплексные сопряженные с отрицательной вещественной частью, то есть
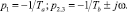(8)
3. Один корень вещественный и отрицательный, а два корня комплексные сопряженные с положительной вещественной частью, то есть
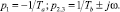(9)
Рис. 1. Переходной процесс в системе при Ta < Tb
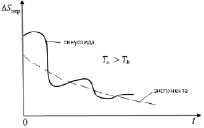
Рис. 2. Переходной процесс в системе при Ta > Tb
Следует отметить, что имеются соответствующие формулы в справочниках по математике, по которым их можно найти и далее вывести очень сложные зависимости Ta, Tb, Tc и ω от параметров системы T0,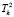 
, Tд, К0, Крег.
Рассмотрим переходные процессы в общем виде для трех вариантов:
а) для первого варианта (7) переходной процесс пойдет по трем экспонентам [1]:
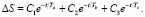(10)
б) для второго варианта (8) – сумма экспонента и затухающая синусоида по экспоненте:
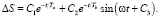(11)
в) для третьего варианта (9) – сумма экспонента и расходящаяся синусоида по экспоненте:
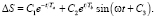(12)
Постоянные интегрирования C1, C2, C3 определяются как обычно из значений начальных условий:
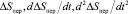при t = 0. (13)
Методика определения C1, C2, C3 такая же, какая была приведена выше, только вместо двух уравнений необходимо решить систему уравнений из трех неизвестных C1, C2, C3.
Для случая (10) переходные процессы будут идти по трем экспонентам.
Для случая (11) переходной процесс зависит от соотношений постоянных времени Ta и Tb.
При Ta < Tb – экспонента затухает быстрее, чем синусоида, и процесс в основном будет колебательным (рис. 1).
Для случая Ta > Tb синусоида затухнет быстрее, чем экспонента, и процесс получается скорее не колебательным, а монотонным, несмотря на наличие комплексных корней характеристического уравнения, еще следует отметить, что это зависит от начальных условий и соотношений постоянного интегрирования С1 и С2 .
Для случая (12) переходной процесс будет колебательным расходящимся, то есть система будет неустойчивой (рис. 3).
Рис. 3. Неустойчивый переходной процесс системы
При получении любого отклонения от равновесного состояния, например, под воздействием возмущающей силы, система не вернется к прежнему значению, будет раскачиваться за счет собственного источника энергии.
Таким образом, можно утверждать, что при всех положительных значениях коэффициентов при переменных в левой части дифференциального уравнения возможна неустойчивость системы.
При этом следует отметить, что положительность всех коэффициентов в левой части дифференциального уравнения системы означает лишь правильность присоединения регулятора к объекту, но этого недостаточно для определения устойчивости системы регулирования. Если параметры регулятора T0, 
, Tд, К0, Крег будут такими, что корни характеристического уравнения будут соответствовать случаю (7), то система будет устойчивой.
Поэтому при проектировании регулятора к объекту необходимо выбрать его параметры таким образом, чтобы система была устойчивой и далее добиваться качества переходного процесса вида (10) или (11) и малого значения статической ошибки.
Статическая ошибка при f(t) = f0 есть частное решении дифференциального уравнения (5) и будет равна
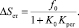(14)
Из формулы (13) видно, что для уменьшения статической ошибки системы регулирования необходимо увеличить Крег – коэффициент усиления регулятора, с другой стороны, имеются определенные ограничения по качествам динамических процессов.
Известны критерии устойчивости Гаусса – Гурвица [5] для системы третьего порядка, дифференциального уравнения который описывается в общем виде (левая часть):
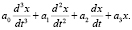(15)
1. Положительность коэффициентов при переменных:
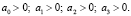(16)
2. Произведение средних коэффициентов должно быть больше, чем произведение крайних коэффициентов:
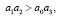(17)
только при выполнении условии (16) и (17) все корни характеристического уравнения (6) будут иметь отрицательные вещественные значения (7) или один корень вещественный отрицательный, а два корня комплексные с отрицательной вещественной частью (8).
Для автоматической системы стабилизации подачи инструмента гидросуппорта согласно дифференциальным уравнениям (5) и (4) имеем
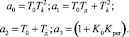(18)
Как было ранее отмечено, первое условие устойчивости (14) обеспечивается правильным присоединением регулятора расхода к объекту.
Условие (16) выводится согласно (17):
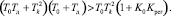(19)
Откуда определяется уравнение ограничение на увеличение коэффициента усиления регулятора Крег:
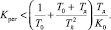(20)
Если сравнить формулы (13) и (18), то обнаружим определенное противоречие между снижением статической ошибки системы и условиями его устойчивой работы, поэтому становится важным учет обоих требований путем подбора приемлемых значений параметров системы, входящих в T0, Tk, Tд, К0, Крег с тем, чтобы значение статической ошибки соответствовало заданному требованию при обеспечении устойчивости системы на заданном диапазоны режимов работ.
Из неравенства (20) можно получить границу устойчивости
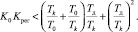(21)
Зная Tk/T0, представляется возможным по (20) построить зависимость K0, Kрег от Tд/Tk (рис. 4).
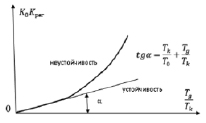
Рис. 4. Граница устойчивости системы
Выводы
1. Разработана математическая модель реальной системы автоматического управления подачей инструмента гидросуппорта, обеспечивающей качественное выполнение технологического процесса механической обработки.
2. Проведено исследование полученной математической модели гидросуппорта, рассмотрено влияние на качество динамических процессов: вид переходного процесса, его длительности и устойчивой работы, значения постоянных времен, куда входят параметры системы.
3. Результаты исследования могут быть использованы при модернизации существующего парка токарных станков и создании нового оборудования.
Библиографическая ссылка
Кадыров И.Ш., Темирбеков Ж.Т., Турусбеков Б.С., Давлятов У.Р. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГИДРОСУППОРТА СТАНКА С АВТОМАТИЧЕСКИМ РЕГУЛЯТОРОМ ВТОРОГО ПОРЯДКА // Международный журнал прикладных и фундаментальных исследований. – 2019. – № 12-1. – С. 115-119;URL: https://applied-research.ru/ru/article/view?id=12965 (дата обращения: 23.11.2024).