Решая задачу о росте сферического дефекта в угольном пласте, мы получили для временной зависимости его радиуса ρ следующее выражение (в случае малых времен):
![]()
где K0 - константа скорости роста дефекта (К0 ≈ 1), АР - избыточное давление, t - время.
В случае больших времен воздействия -
где а - температуропроводность угля, Q - скрытая теплота (энтальпия) угля.
Таким образом, при малых временах воздействия t скорость процесса определяется кинетикой роста дефекта. При увеличении t роль диссипации механической энергии возрастает и, наконец, делается решающей. Рассматривая далее слияние дефектов с позиций классической статистической физики, для длины трещины L мы получили следующее выражение:
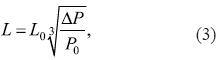
Рассмотрим конкретный пример. Время распространения трещины в угольном пласте определяется скоростью распространения звука и имеет порядок t ≈ 107 с, при максимальном давлении ΔР = 600 МПа имеем:
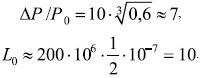
Тогда L ≈ 70 м. Основатель гидроразрыва угольного пласта Н.В. Ножкин дает значения L от 30 до 120 м [1]. Полученное нами значение
лежит в этом интервале. Это говорит о том, что формулу (3) можно применять для определения параметров гидроразрыва пласта.
Список литературы
1. Ножкин Н.В. Заблаговременная дегазация угольных месторождений. - М.: Недра, 1979. - 271 с.
Библиографическая ссылка
Таткеева Г.Г., Юров В.М. ОПРЕДЕЛЕНИЕ ДЛИНЫ ТРЕЩИНЫ ПРИ ГИДРАВЛИЧЕСКОМ РАЗРЫВЕ УГОЛЬНОГО ПЛАСТА // Международный журнал прикладных и фундаментальных исследований. 2011. № 6. С. 153-153;URL: https://applied-research.ru/ru/article/view?id=1302 (дата обращения: 13.02.2026).

