Теория и применение сингулярно-возмущенных систем дифференциальных уравнений в настоящее время активно развивается и применяется для решения широкого круга задач в различных отраслях науки. Такие системы появляются естественным образом в процессе моделирования и исследования объектов различной природы, способных одновременно совершать быстрые и медленные движения.
В сингулярно-возмущенных задачах эти системы являются жесткими и, как следствие, при вычислениях возникают серьезные трудности, выражающиеся в недопустимо большом времени счета и неизбежном накоплении вычислительных ошибок. Поэтому возрастает роль асимптотических методов, тем более, что при их применении происходит декомпозиция исходной задачи оптимального управления на задачи меньшей размерности.
Задачи оптимизации таких систем в различных постановках исследовались многими авторами [1]. Следует отметить, что нахождение допустимого управления с использованием метода разделения движений относится к перспективным методам оптимального управления [2–4]. Задача разделения движений сингулярно-возмущенной управляемой системы были предметом исследования и в наших работах [5, 6].
Данная работа посвящена построению асимптотических приближений к решению задачи оптимизации переходного процесса в линейной сингулярно-возмущенной системе. Эта задача состоит в нахождении допустимого управления с минимальными энергетическими затратами [7, 8] и построении оптимальной траектории обладающей магистральными свойствами [9]. Такие исследования начаты относительно давно, но сохраняют свою актуальность по настоящее время, о чем свидетельствуют новейшие работы, на эту тему в различной постановке [10–12].
Постановка задачи
Пусть управляемый процесс описывается сингулярно-возмущенной системой вида
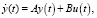 (1)
(1)
где
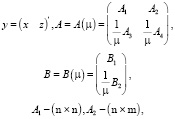
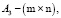
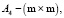
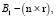
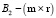 – постоянные матрицы,
– постоянные матрицы, 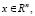
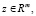
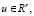
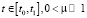 – малый параметр, штрих обозначает транс- понирование.
– малый параметр, штрих обозначает транс- понирование.
Рассмотрим задачу перевода объекта (1) из некоторого состояния
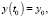 (2)
(2)
в состояние
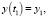 (3)
(3)
при этом функционал
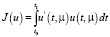 (4)
(4)
принимал наименьшее возможное значение.
Предполагается, что система (1) вполне управляема. Функционал (4) можно рассматривать как квадрат нормы функции u(t) в пространстве 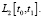 Так как норма
Так как норма 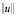 достигает минимума со своим квадратом в
достигает минимума со своим квадратом в 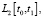 то необходимо выбрать среди допустимых решений задачи программного управления (задача о переводе системы (1) из заданной начальной точки (2) в конечную точку (3)) такое решение, которое имеет минимальную норму в
то необходимо выбрать среди допустимых решений задачи программного управления (задача о переводе системы (1) из заданной начальной точки (2) в конечную точку (3)) такое решение, которое имеет минимальную норму в 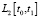 [13].
[13].
Такое решение (с минимальной нормой) существует, если компоненты импульсной переходной вектор-функции линейно независимы и это условие выполняется, если заданная система вполне управляема [13]. По предположению система (1) вполне управляема.
Предположим также, что корни характеристического уравнения матрицы A4 удовлетворяют неравенству
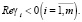 (5)
(5)
В управляемых системах функционал (4) используется как критерий минимума затрат энергии на управление [13]. Поэтому данную задачу с минимальной нормой, иначе назовем задачей с минимальной энергией.
При выполнении условий (5), как показано в [2] систему (1) можно заменить эквивалентной системой, у которой разделены медленные x(t) и быстрые z(t) составляющие вектора состояния:
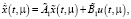 (6)
(6)
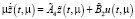
где
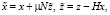 (7)
(7)
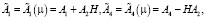
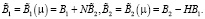
Матрицы 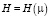 и
и 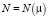 определяются из уравнения:
определяются из уравнения:
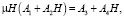 (8)
(8)
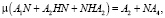
Граничные условия системы (6) определяются соотношениями:
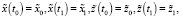 (9)
(9)
где
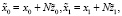
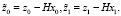
Теперь сформулируем задачу об управлении с минимальной энергией для системы (6) следующим образом: требуется найти управление 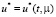 среди всех допустимых управлений доставляющие минимум функционалу (4) при ограничениях (6), (7).
среди всех допустимых управлений доставляющие минимум функционалу (4) при ограничениях (6), (7).
При μ = 0 из (1) получаем
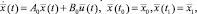 (10)
(10)
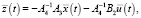
где 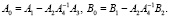
Задача (4), (10) является предельной к задаче (1)–(4). Поведение системы (1) или (6) в окрестности граничных точек существенно отличается от поведения системы (10). Поэтому рассмотрим систему
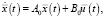 (11)
(11)
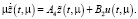
Система (11) аппроксимирует систему (1) с точностью порядка μ, т.е. она является асимптотической с точностью О(μ) и получается из (6) при следующих приближениях:
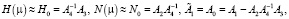 (12)
(12)
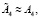
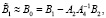
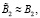
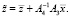
Граничные условия системы (11) определяются соотношениями:
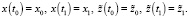 (13)
(13)
Заметим, что системы (10) и (11) отличаются только вторыми уравнениями. Поэтому решение задачи (4), (6), (7) построим для системы (11). Поправка к первому приближению не представляет трудности, т.е. все изложенные процедуры для системы (11) аналогично повторяются для высших приближений. Следует заметить, что быстрая подсистема системы (11) рассматривается на большом промежутке времени, поэтому коэффициенты этой подсистемы считаются медленно меняющимся функциями [14].
Решение задачи
Решения системы (11) можно представить в виде
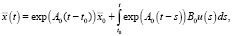 (14)
(14)
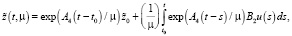 (15)
(15)
где 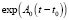 – переходная матрица медленной подсистемы (11).
– переходная матрица медленной подсистемы (11).
В силу соотношения (14) ограничение 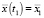 приводит к тому, что искомое управление
приводит к тому, что искомое управление 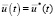 должно удовлетворять условию
должно удовлетворять условию
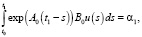 (16)
(16)
где 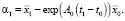
Управление 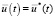 удовлетворяющее моментному соотношению (16) и доставляющее минимум функционалу (4), определяется формулой [13]
удовлетворяющее моментному соотношению (16) и доставляющее минимум функционалу (4), определяется формулой [13]
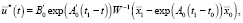 (17)
(17)
где 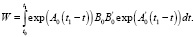
Тогда оптимальные траектории 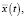
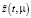 системы (11), соответствующее оптимальному управлению (17) записываются в виде:
системы (11), соответствующее оптимальному управлению (17) записываются в виде:
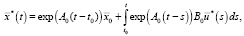 (18)
(18)
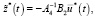 (19)
(19)
где 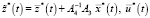 определяется из (17).
определяется из (17).
При t = t0 и t = t1 из (19) получаем:
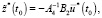
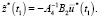 (20)
(20)
В силу соотношений (15), (19), (20) разность векторов 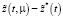 определяет оптимальную траекторию задачи (4), (11), (13) в форме
определяет оптимальную траекторию задачи (4), (11), (13) в форме
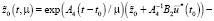 (21)
(21)
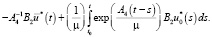
Для задачи (4), (11), (13) определим управление в виде
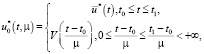 (22)
(22)
где 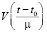 – пограничная функция, которая имеет экспоненциальный характер убывания.
– пограничная функция, которая имеет экспоненциальный характер убывания.
Управление 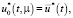 имеющее минимальную норму и переводящее медленную подсистему (11) из начального состояния x(t0) = x0 в конечное состояние x(t1) = x1 известно. Теперь остается построить управление
имеющее минимальную норму и переводящее медленную подсистему (11) из начального состояния x(t0) = x0 в конечное состояние x(t1) = x1 известно. Теперь остается построить управление 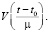
При t = t1 с учетом (4), (22) из (21) получим
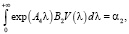 (23)
(23)
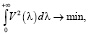 (24)
(24)
где
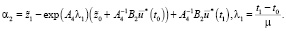 (25)
(25)
Решение задачи (23), (24) согласно проблемы моментов записывается в виде [13]
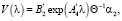 (26)
(26)
где
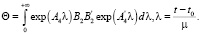 (27)
(27)
Управление 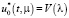 переводит быструю подсистему систем (11) из начального состояния
переводит быструю подсистему систем (11) из начального состояния 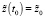 в конечное состояние
в конечное состояние 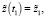 имеет минимальную норму и при λ→+∞ (μ→0) стремится к нулю.
имеет минимальную норму и при λ→+∞ (μ→0) стремится к нулю.
С учетом (26) из (21) будем иметь
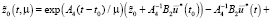 (28)
(28)
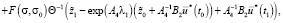
где 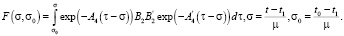
Матрица F(t, t0) в (28) удовлетворяет матричному дифференциальному уравнению [15]
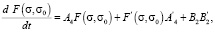
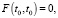 (29)
(29)
По условию (5) A4 – устойчивая матрица, поэтому несобственный интеграл в (27) сходится и является единственным решением алгебраического матричного уравнения [15]
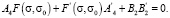 (30)
(30)
Введем в (29) замену переменной
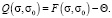 (31)
(31)
Тогда с учетом (30) из (29) имеем
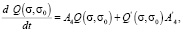
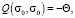 (32)
(32)
Решение матричного уравнения (32) имеет вид [15]
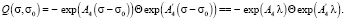 (33)
(33)
Тогда с учетом замены (31)
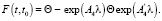 (34)
(34)
Подставляя (34) в (28) получаем
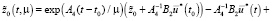 (35)
(35)
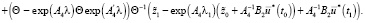
Оптимальная траектория 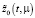 удовлетворяет всем граничным условиям (13) и для нее имеет место следующее предельное соотношение
удовлетворяет всем граничным условиям (13) и для нее имеет место следующее предельное соотношение
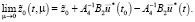
Траектория функции
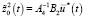 (36)
(36)
формирует «магистраль». Оптимальная траектория процесса, выходя из начальной точки направляется к магистрали, и в течении достаточно долгого времени находится вблизи этой линии (при достаточно малых μ), и уходит с неё для достижения заданного конечного состояния.
Введем следующие значения параметров системы (1):
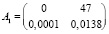 ,
, 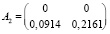 ,
, 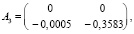
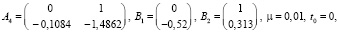
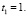
Корни характеристического уравнения матрицы A4 удовлетворяют неравенству (5):
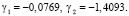
Согласно (12) находим: 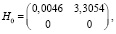
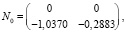
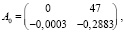
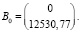
Находим переходную матрицу 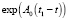 , используя преобразования Лапласа [15]:
, используя преобразования Лапласа [15]:
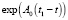
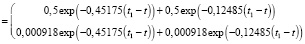 (37)
(37)
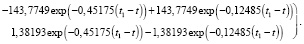
Далее вычисляем элементы матриц W из (17) при t0 = 0, t1 = 1:
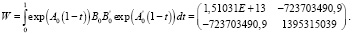
При фиксированных начальных и конечных условиях:
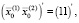
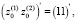 (38)
(38)
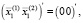
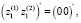 (39)
(39)
согласно (17) получаем оптимальное управление 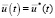 имеющее минимальную норму и переводящее медленную подсистему (11) из начального состояния (38) в конечное состояние (39):
имеющее минимальную норму и переводящее медленную подсистему (11) из начального состояния (38) в конечное состояние (39):
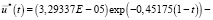
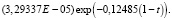 (40)
(40)
Теперь построим управление 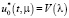 , которые переводит быструю подсистему систем (11) из начального состояния
, которые переводит быструю подсистему систем (11) из начального состояния
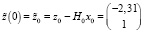 (41)
(41)
в конечное состояние
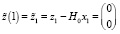 (42)
(42)
имеет минимальную норму и при λ→+∞ (μ→0) стремится к нулю.
Переходная матрица 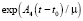 и α2 из (25) при μ = 0,01, t0 = 0, t1 = 1 имеют вид:
и α2 из (25) при μ = 0,01, t0 = 0, t1 = 1 имеют вид:
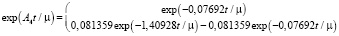
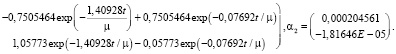 (43)
(43)
Далее вычисляем Θ из (26) и Θ-1:
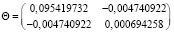 ,
, 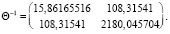
Управление 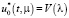 , которые переводит быструю подсистему систем (11) из начального состояния (41) в конечное состояние (42) согласно (26) записываем в виде
, которые переводит быструю подсистему систем (11) из начального состояния (41) в конечное состояние (42) согласно (26) записываем в виде
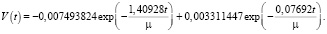 (44)
(44)
Магистраль 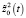 и пограничные функции
и пограничные функции 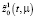 и
и 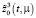 имеют вид:
имеют вид:
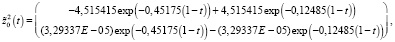 (45)
(45)
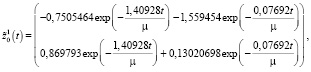 (46)
(46)
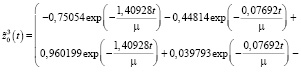 (47)
(47)

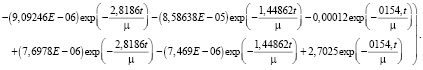
Результаты моделирование оптимального управления 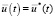 имеющее минимальную норму и переводящее медленную подсистему (11) из начального состояния (38) в конечное состояние (39) согласны (40) показаны на рис. 1.
имеющее минимальную норму и переводящее медленную подсистему (11) из начального состояния (38) в конечное состояние (39) согласны (40) показаны на рис. 1.
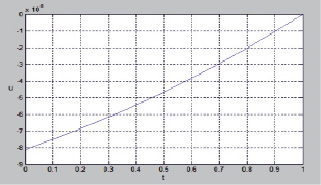
Рис. 1. Оптимальное управление медленной подсистемы
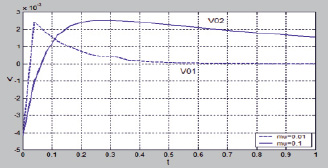
Рис. 2. Оптимальное управление быстрой подсистемы
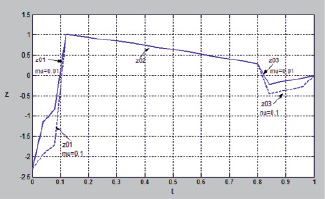
Рис. 3. Оптимальная траектория процесса
Результаты моделирование оптимального управления 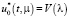 , которые переводит быструю подсистему систем (11) из начального состояния (41) в конечное состояние (42) согласно (44), при различных значениях параметра μ(μ = 0,01 и μ = 0,1) приведены на рис. 2.
, которые переводит быструю подсистему систем (11) из начального состояния (41) в конечное состояние (42) согласно (44), при различных значениях параметра μ(μ = 0,01 и μ = 0,1) приведены на рис. 2.
Результаты моделирования оптимальных траекторий соответствующие оптимальным управлениям (40) и (44) приведены на рис. 3.
Таким образом, оптимальная траектория 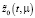 состоит из трех составляющих первое из них
состоит из трех составляющих первое из них 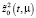 из (45) формирует «магистраль», остальные две пограничные функции:
из (45) формирует «магистраль», остальные две пограничные функции: 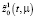 и
и 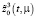 соответственно описывают переходы от начального состояния на магистраль и с магистрали в конечное состояние.
соответственно описывают переходы от начального состояния на магистраль и с магистрали в конечное состояние.
Заключение
В данной работе предложен способ решения сингулярно-возмущенной задачи оптимального управления при минимума квадратичного функционала, который оценивает энергии управляющего воздействия. Для данной задачи предложен эффективный алгоритм нулевого равномерного асимптотического приближенного решения на основе совместного использования методов разделения движений и проблемы моментов.
Библиографическая ссылка
Иманалиев З.К., Аширбаев Б.Ы. АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ СИНГУЛЯРНО-ВОЗМУЩЕННОЙ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ С МИНИМАЛЬНОЙ ЭНЕРГИЕЙ // Международный журнал прикладных и фундаментальных исследований. 2020. № 3. С. 89-97;URL: https://applied-research.ru/ru/article/view?id=13041 (дата обращения: 17.12.2025).
DOI: https://doi.org/10.17513/mjpfi.13041

