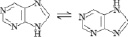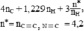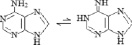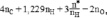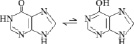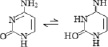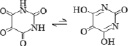Стандартные аминокислоты, входящие в состав белков, и гетероциклические азотсодержащие основания, входящие в состав нуклеиновых кислот, относятся к наиболее значимым компонентам всех живых организмов. Соответствие последовательности нуклеотидов в биополимерах РНК и ДНК с последовательностью аминокислот в биополимерах белка определяет генетический код [1]. При обсуждении проблемы возникновения генетического кода отмечена важность изучения факторов дифференцированного отбора протобиомономеров и особенностей пребиотического синтеза при абиогенезе и начальных биогенных стадиях [2]. В древних гидротермальных системах с CO, CO2, H2, NH3, CH4, H2S и H2O могли синтезироваться пребиотические молекулы формальдегида и циановодорода, затем из их смесей мог осуществляться абиогенный синтез углеводов, аминокислот и азотистых оснований [3, 4]. Предполагается возможность пребиотического синтеза азотистых оснований при облучении ультрафиолетом пиримидина и пурина в холодных астрофизических условиях на первобытной Земле и других космических объектах Вселенной [5–7].
В этом плане особый интерес представляет собой изучение термохимии аминокислот и азотистых оснований, взаимосвязи между их структурой и энергетикой. Широко практикуется экспериментальное определение энергии сгорания ряда чистых биоорганических соединений в калориметрической бомбе с газообразным кислородом до CO2, H2O, N2 и H2SO4 [8]. Эти анализы сопряжены с рядом технических сложностей и могут иметь существенные расхождения. Поэтому при изучении термохимии сгорания биологически важных мономеров особое значение приобретают расчетные методы [9–11]. Обычно для приближенных оценок изменения стандартной энтальпии той или иной реакции (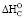 ) используют эмпирические значения энергетических вкладов одинарных и кратных связей атомов, групп атомов в резонансных структурах.
) используют эмпирические значения энергетических вкладов одинарных и кратных связей атомов, групп атомов в резонансных структурах.
Цель работы: приближенные вычисления значений стандартных энтальпий сгорания протеиногенных аминокислот и азотистых оснований по их элементному составу и пространственной структуре.
Возможность оценки изменений свободной энергии и энтальпии сгорания биохимических соединений на основе их элементного состава
Внутренняя энергия системы может изменяться при совершении работы или в процессе передачи энергии в виде теплоты (∆H, энтальпия, теплосодержание, тепловая функция Гиббса) [8]. Для характеристики самопроизвольных (необратимых) биохимических процессов, протекающих при постоянных температуре и давлении, принято использовать изменение свободной энергии Гиббса:
∆GT,P = ∆H – T∙∆S,
где ∆S – изменение энтропии, T – термодинамическая температура.
При сгорании питательных веществ ∆H обычно значительно больше T∙∆S, поэтому она не очень сильно отличается от ∆G и может служить приблизительной мерой совершаемой работы. Число электронов (ne), участвующих в полном окислении вещества, рассчитывают исходя из числа атомов в молекуле данного вещества (nC, nH, nS, nO) и соответствующей им валентности [8]:
ne = 4nC + nH + 6nS – 2nO.
Анализ стандартных значений термодинамических величин ∆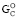 и ∆
и ∆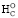 позволяет полнее понять сущность структурных единиц соединений (атомов, ядер, электронов), связь атомов друг с другом и взаимодействие групп атомов в молекуле.
позволяет полнее понять сущность структурных единиц соединений (атомов, ядер, электронов), связь атомов друг с другом и взаимодействие групп атомов в молекуле.
В электрохимии изменение свободной энергии Гиббса принято выражать через электродные потенциалы, связанные с переносом электронов через границу между гальваническим электродом и электролитом при прохождении электрического тока [8]. В этом случае используют функциональную связь ∆GO со стандартной разностью окислительно-восстановительных потенциалов ∆EO (при pH7, 25 °C) сопряженных пар окислитель-восстановитель:
∆GO = –∆EO(B)∙ne∙F (Кл∙моль-1) =
= –ne∙∆EO∙96,485 кДж∙моль-1,
где F – число Фарадея, ne – число электронов, переносимых от восстановителя к окислителю.
По шкале электродных потенциалов значение ∆EO полуреакции кислород-водород (O2 + 4H+ + 4e → 2H2O) равен +1,229 В. Следовательно, максимальная работа (–∆GO), которую может совершить поток электронов во внешней цепи, обусловленной электрохимической реакцией кислород-водород, составляет:
∆GO = –2∙1,229 (В)∙96,485 (Кл∙моль-1) =
= –237,16 кДж∙моль-1.
С другой стороны, из калориметрических данных стандартная свободная энергия сгорания H2 (∆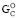 ) тоже равна – 237,2 кДж∙моль-1.
) тоже равна – 237,2 кДж∙моль-1.
Окислительно-восстановительным парам O2–H2O и H+–H2 в биохимическом отношении принадлежит исключительно важная роль [8]. Между ними располагается множество других пар окислительно-восстановительных реакций живой клетки. Учитывая значение электродного потенциала электрохимической реакции кислород-водород (∆EO 1,229 В), количественный состав атомов в биологически важных соединениях (nC, nH, nS, nO) и соответствующие им валентности можно приближенно оценить ∆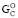 и теплоту сгорания ∆
и теплоту сгорания ∆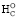 по следующему эмпирическому уравнению:
по следующему эмпирическому уравнению:
–96,485 [4nC + 1,229nH + 6nS – ≤ 2nO].
При сгорании органических соединений (ОС) происходит перемещение валентных электронов от атомов углерода, водорода и серы к атомам экзогенного газообразного кислорода. При сгорании ОС, богатых атомами кислорода, в калориметрической бомбе будет расходоваться меньше газообразного кислорода и бомба будет меньше выделять в окружающую среду тепла (–Qv). При замещении атомов водорода, связанных с углеродом, атомами кислорода или группами кислородсодержащих атомов (–COH, –CHO, –C=O, –COOH) изменяется состав и электронная структура молекулы, и, следовательно, уменьшается теплота сгорания ОС. Поэтому расчет ∆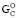 , ∆
, ∆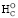 и количества электронов (ne), участвующих в полном окислении представителей различных классов кислородных ОС, можно осуществить путем внесения поправки в единственный параметр ≤ –2nO.
и количества электронов (ne), участвующих в полном окислении представителей различных классов кислородных ОС, можно осуществить путем внесения поправки в единственный параметр ≤ –2nO.
Расчет ∆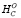 протеиногенных аминокислот
протеиногенных аминокислот
Стандартные аминокислоты белков представляют собой карбоновые кислоты с альфа-аминогруппой –NH2, присоединенной к атому углерода, связанного с карбоксильной группой –COOH. Они различаются между собой структурой «боковых цепей». Определенные α-аминокислоты имеют дополнительную карбоксильную (Asn, Gln) или аминогруппу (Asn, Gln), –OH или –SH-группу (Ser, Thr, Tyr, Cys), ароматические (Phe, Tyr) или азотсодержащие гетероциклы (Pro, His, Trp). Из-за различий в элементном составе и электронной структуре α-аминокислот уравнения оценки их ∆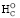 отличаются значением поправки в параметре ≤ –2nO (табл. 1).
отличаются значением поправки в параметре ≤ –2nO (табл. 1).
Таблица 1
Экспериментальные и расчётные стандартные значения свободной энергии (∆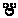 ) и энтальпии (∆
) и энтальпии (∆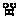 ) сгорания протеиногенных аминокислот, кДж·моль-1
) сгорания протеиногенных аминокислот, кДж·моль-1
|
Аминокислота, кодоны и формула |
Литературные данные |
Расчётное – ∆ |
Уравнение ∆ |
|||
|
– ∆ |
– ∆ |
|||||
|
1 |
2 |
3 |
4 |
5 |
||
|
#1 Gly |
|
NH2 – CH2 – COOH |
1008,3 |
966,1 [13]; 973,0 [14]; 973,1 [14, 15]; 974,1 [9]; 975,0 [11]; 977,6 [16] |
978,8 |
4nC + 1,229nH – 2nO |
|
#2 Ala |
|
|
1642,0 |
1577,0 [13]; 1608,4 [16]; 1621,5 [10,14]; 1622,9 [20] |
1601,9 |
То же |
|
#3 Asp |
GAUC |
|
1690,1 |
1598,6 [16]; 1599,0 [10]; 1600,4 [17]; 1601,1 [9] |
1601,9 |
То же |
|
#11 Asn |
AAUC |
|
1999,7 |
1906,6 [10]; 1928,5 [22] |
1913,5 |
То же |
|
#5 Glu |
GAAG |
|
2314,7 |
2228,3 [16]; 2248,5 [9]; 2250,5 [18]; 2251,9 [10] |
2225,0 |
То же |
|
#14 Gln |
CAAG |
|
2633,1 |
2558,9 [10]; 2572,3 [23] |
2565,5 |
4nC + 1,229nH – 1,9nO |
|
#8 Thr |
|
|
2130,3 |
2053,9 [13]; 2071,9 [10]; 2084,6 [11]; 2101,5 [9] |
2061,0 |
То же |
|
#6 Ser |
|
|
1507,1 |
1426,0 [10]; 1441,9 [9]; 1446,3 [16]; 1448,2 [21] |
1437,9 |
То же |
|
#19 Cys |
UGUC |
|
2178,3 |
2235,3 [10]; 2248,8 [19] |
2238,7 |
4nC + 1,229nH + 6nS – 1,7nO |
|
Цистин C6H12O4N2S2 |
|
4133,8 |
4248,0 [11] |
4240,3 |
То же |
|
|
Окончание табл. 1 |
||||||
|
1 |
2 |
3 |
4 |
5 |
||
|
#4 Val |
|
|
2936,5 |
2919,9 [10]; 2920,1 [23]; 2922,7 [9] |
2925,3 |
4nC + 1,229nH – 1,6nO |
|
#15 Lys |
|
|
3691,6 |
3683,2 [9] |
3686,3 |
4nC + 1,229nH – 1,5nO |
|
#12 Ile |
|
|
3574,1 |
3572,1 [10]; 3578,3 [13]; 3583,7 [9] |
3577,4 |
4nC + 1,229nH – 1,45nO |
|
#9 Leu |
|
|
3571,7 |
3569,3 [23]; 3572,7 [10]; 3578,4 [9]; 3581,5 [15] |
3577,4 |
То же |
|
#7 Pro |
|
|
2764,1 |
2727,8 [10]; 2738,6 [24]; 2746,2 [25] |
2736,4 |
4nC + 1,229nH – 1,35nO |
|
#10 Arg |
|
|
3762,9 |
3724,2 [16]; 3738,3 [15]; 3740,7 [10] |
3734,5 |
4nC + 1,229nH – 1,25nO |
|
#18 Tyr |
UAUC |
|
4466,8 |
4413,3 [10]; 4419,8 [16]; 4428,1 [15] |
4416,0 |
То же |
|
#13 His |
CAUC |
|
3259,7 |
3180,6 [26]; 3195,6 [27]; 3205,5 [25]; 3212,0 [16]; 3220,3 [10] |
3209,2 |
4nC + 1,229nH – 0,9nO |
|
#17 Phe |
UUUC |
|
4646,1 |
4627,3 [10]; 4637,5 [16]; 4646,3 [13] |
4642,8 |
4nC + 1,229nH – 0,7nO |
|
#20 Trp |
UGG |
|
5623,2 |
5615,7 [10]; 5628,3 [17]; 5629,6 [13] |
5620,1 |
4nC + 1,229nH – 0,25nO |
Уравнения вычисления ∆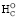 для 11-ти С2–С5 аминокислот аналогичны таковым для карбоновых кислот и спиртов (кДж∙моль-1):
для 11-ти С2–С5 аминокислот аналогичны таковым для карбоновых кислот и спиртов (кДж∙моль-1):
∆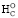 = –96,485 [4nC + 1,229nH – (2,0÷1,6)nO].
= –96,485 [4nC + 1,229nH – (2,0÷1,6)nO].
В уравнениях оценки ∆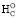 для 6-ти С5–С11 аминокислот с кратными связями (Arg и циклические) параметр –2nO замещен на –(1,35÷0,25)nO. Наиболее существенная поправка (–0,25nO) внесена в уравнение ∆
для 6-ти С5–С11 аминокислот с кратными связями (Arg и циклические) параметр –2nO замещен на –(1,35÷0,25)nO. Наиболее существенная поправка (–0,25nO) внесена в уравнение ∆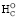 для единственного бициклического наиболее высокомолекулярного триптофана (C11H12O2N2). Поэтому число электронов, участвующих в полном окислении Trp в микрокалориметре за счет газообразного кислорода, будет максимальным и достигать 55,5
для единственного бициклического наиболее высокомолекулярного триптофана (C11H12O2N2). Поэтому число электронов, участвующих в полном окислении Trp в микрокалориметре за счет газообразного кислорода, будет максимальным и достигать 55,5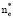 , превышая соответствующее значение 52,0ne по литературным данным [8].
, превышая соответствующее значение 52,0ne по литературным данным [8].
Вычисление ∆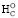 α-аминокислот можно производить с аналогичной хорошей точностью и по следующему эмпирическому уравнению (кДж∙моль-1):
α-аминокислот можно производить с аналогичной хорошей точностью и по следующему эмпирическому уравнению (кДж∙моль-1):
∆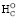 = –96,485 [n* + 0,229nH].
= –96,485 [n* + 0,229nH].
Для большинства протеиногенных аминокислот стандартная энергия сгорания ∆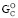 превышает ∆
превышает ∆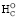 , так как у них изменение энтропии ∆
, так как у них изменение энтропии ∆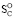 имеет положительное значение и работа по изменению объема окружения незначительна [11, 12]. В этом случае приближенную оценку ∆
имеет положительное значение и работа по изменению объема окружения незначительна [11, 12]. В этом случае приближенную оценку ∆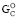 по эмпирическому уравнению можно произвести путем сокращения значения параметра ≤ –2nO до –(1,80÷1,95)nO. Значение ∆
по эмпирическому уравнению можно произвести путем сокращения значения параметра ≤ –2nO до –(1,80÷1,95)nO. Значение ∆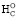 существенно превышает ∆
существенно превышает ∆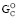 (на 2,6–2,8 %) лишь у серусодержащих метионина, цистеина и цистина [8, 11, 19]. В этом случае при расчете ∆
(на 2,6–2,8 %) лишь у серусодержащих метионина, цистеина и цистина [8, 11, 19]. В этом случае при расчете ∆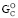 параметр –1,7nO (для ∆
параметр –1,7nO (для ∆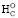 ), напротив, следует повысить до –2nO. Значение ∆
), напротив, следует повысить до –2nO. Значение ∆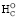 несколько превышает ∆
несколько превышает ∆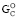 (~ на 0,1 %) и у C6 углеводородных аминокислот лейцина и изолейцина (C6H13O2N), имеющих отрицательное значение ∆
(~ на 0,1 %) и у C6 углеводородных аминокислот лейцина и изолейцина (C6H13O2N), имеющих отрицательное значение ∆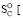 8–15].
8–15].
Следует отметить тот факт, что в хронологии появления определенных α-амино- кислот в биополимерах белка (от #1Cys до #20Trp) и соответствующим им составом кодонов просматривается определенная согласованность с параметром ≤ –2nO (от –2nO до –0,25nO) в таблице расчета ∆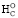 . В корне кодонов для первых С2–С5 аминокислот (#1, 2, 3, 5, 8, 11, 14) в первой позиции доминирует гуанин (GI), а во второй позиции аденин (AII), но отсутствует урацил. Напротив, урацил содержится в первой позиции кодонов (UI) для C3 серусодержащей спирто-аминокислоты #19Cys (UGUC), для C9 и C11 циклических аминокислот #17Phe (UUUC), #18Tyr (UAUC), #20Trp (UGG), для неканонических аминокислот C3 спирто-аминокислоты селеноцистеина #21SeC (UGA) [38], C12 пирролизина #22Pyl (UAG) [39] и у стоп-кодонов (UGA, UAAG). Из состава этих однократных и двукратных кодонов с UI для #17–22 аминокислот и терминирующих кодонов исключен цитозин [2].
. В корне кодонов для первых С2–С5 аминокислот (#1, 2, 3, 5, 8, 11, 14) в первой позиции доминирует гуанин (GI), а во второй позиции аденин (AII), но отсутствует урацил. Напротив, урацил содержится в первой позиции кодонов (UI) для C3 серусодержащей спирто-аминокислоты #19Cys (UGUC), для C9 и C11 циклических аминокислот #17Phe (UUUC), #18Tyr (UAUC), #20Trp (UGG), для неканонических аминокислот C3 спирто-аминокислоты селеноцистеина #21SeC (UGA) [38], C12 пирролизина #22Pyl (UAG) [39] и у стоп-кодонов (UGA, UAAG). Из состава этих однократных и двукратных кодонов с UI для #17–22 аминокислот и терминирующих кодонов исключен цитозин [2].
Расчет ∆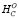 азотистых оснований
азотистых оснований
Гетероциклические азотистые основания, входящие в природные нуклеотидные последовательности, построены на основе плоских кольцевых структур шестичленного пиримидина C4H4N2 или бициклического пурина C5H4N4. Главные и минорные азотистые основания различаются наличием (или отсутствием) боковых карбоксильных (C=O) и/или аминогрупп (NH2), замещающих в замкнутых циклах атомы водорода. Однако все C4 шестичленные кольца пиримидинов и C5 сопряженные шести- и пятичленные (имидазольные) кольца пуринов содержат одну C=C связь и по два атома азота в C–N и C=N связях.
Согласно теории резонанса, циклические молекулы ароматических и азотистых оснований описывают как суперпозицию (наложение) двух и более валентных структур, эквивалентных, но с обратным наложением одинарной и двойной связи [8, 12]. Переход одной резонансной формы в другую сопровождается перераспределением валентных электронов, но все ядра элементов остаются на прежних местах. Кольцевые молекулы с гибридными электронными структурами приобретают дополнительную стабилизирующую энергию резонанса и, следовательно, пониженную химическую реакционную способность.
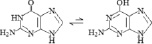
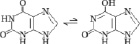
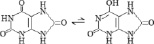
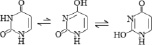
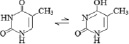
Природные пуриновые и пиримидиновые основания с заместителями существуют в виде смеси двух и более изомеров, таутомерных форм, быстро преходящих одна в другую (табл. 2). В паре таутомеров один из атомов водорода легко переходит из одного положения в другое, что сопровождается изменением длин и характера других связей [1, 8]. Переходы атомов водорода осуществляются через замещающие боковые карбонильные и аминные группы. В молекулах аденина и цитозина таутомерное равновесие устанавливается между амино- и иминоформами, в гуанине, урациле и тимине – между кето-енольными формами. В составе нуклеозидов основания существуют фактически в более устойчивых кето- и аминоформах. Тем самым у азотистых оснований с замещающими группами между резонансной стабилизацией и таутомерной диссоциацией атома водорода просматривается тесная структурная и функциональная связь.
Таблица 2
Экспериментальные и расчётные значения стандартной энтальпии сгорания азотистых оснований, кДж·моль-1
|
Соединение и формула |
Опытное –∆ |
Расчётное значение |
Уравнение ∆ |
|
|
1 |
2 |
3 |
4 |
|
|
Пурин C5H4N4 |
|
2708,6 [29] |
2708,0 |
|
|
Аденин C5H5N5 |
|
2764,9 [32]; 2777,1 [31]; 2779,0 [30] |
2765,7 |
То же |
|
Гуанин C5H5ON5 |
|
2497,4 [ 31] |
2503,3 |
n* = 3,0 |
|
Гипоксантин C5H4ON4 |
|
2427,6 [ 31] |
2428,1 |
То же |
|
Ксантин C5H4O2N4 |
|
2159,0 [ 31] |
2162,8 |
То же, n* = 2,0 |
|
1 |
2 |
3 |
4 |
|
|
Мочевая кислота C5H4O3N4 |
|
1919,8 [31] |
1919,2 |
То же, n* = 1,3 |
|
Цитозин C4H5ON3 |
|
2053,2 [34]; 2064,8 [33]; 2066,7 [35]; 2067,3 [26] |
2059,5 |
То же, n* = 2,0 |
|
Урацил C4H4O2N2 |
|
1715,2 [36]; 1716,3 [33]; 1721,3 [26] |
1719,0 |
То же, n* = 1,2 |
|
Тимин (5-Метилурацил) C5H6O2N2 |
|
2359,3 [36]; 2359,8 [33]; 2367,3 [35]; 2371,2 [37] |
2363,8 |
То же, n* = 1,5 |
|
Аллоксан C4H2O4N2 |
|
1144,7 [31] |
1153,8 |
То же, n* = 1,0 |
При расчете теплоты сгорания гетероциклических оснований по их элементному составу и пространственной структуре необходимо учитывать число перемещаемых валентных электронов от атомов углерода и водорода к атомам газообразного кислорода, а также количество двойных связей C=N и C=C в резонансных структурах. Во всех таутомерных кислородсодержащих основаниях, существующих преимущественно в кетоформах с C=O группами, число перемещаемых к экзогенному молекулярному кислороду электронов целесообразно уменьшить на одинаковую величину –2nO.
Значение ∆ при сгорании азотистых оснований можно рассчитать с хорошей точностью по следующему эмпирическому уравнению (кДж∙моль-1):
при сгорании азотистых оснований можно рассчитать с хорошей точностью по следующему эмпирическому уравнению (кДж∙моль-1):
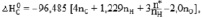
где дополнительный параметр 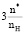 учитывает общее количество кратных связей C=N и C=C в резонансной структуре (n*) и валентность атомов азота по отношению к содержанию атомов водорода в соединении (nH). Для бициклических пуриновых оснований, не содержащих атомов кислорода (пурин и аденин), –2nO = 0 и n* = 4,2 (
учитывает общее количество кратных связей C=N и C=C в резонансной структуре (n*) и валентность атомов азота по отношению к содержанию атомов водорода в соединении (nH). Для бициклических пуриновых оснований, не содержащих атомов кислорода (пурин и аденин), –2nO = 0 и n* = 4,2 (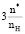 = 3,15 – 2,52), но для мочевой кислоты C5H4O3N4 с наибольшим количеством атомов кислорода значение –2nO = –6 и n* = 1,3 (
= 3,15 – 2,52), но для мочевой кислоты C5H4O3N4 с наибольшим количеством атомов кислорода значение –2nO = –6 и n* = 1,3 (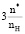 = 0,98). При этом расчетное ∆
= 0,98). При этом расчетное ∆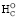 отличается от средних экспериментальных значений [29–32] на 0,02–0,28 %. Также для главных моноциклических кислородсодержащих пиримидиновых оснований расчетное ∆
отличается от средних экспериментальных значений [29–32] на 0,02–0,28 %. Также для главных моноциклических кислородсодержащих пиримидиновых оснований расчетное ∆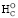 отличается от средних экспериментальных значений [26, 33–37] на 0,03–0,17 % (табл. 2). Для цитотоксичного вещества аллоксана C4H2O4N2 с максимально допустимым содержанием атомов кислорода у пиримидиновых таутомеров значение –2nO = –8 и n* = 1,0 (
отличается от средних экспериментальных значений [26, 33–37] на 0,03–0,17 % (табл. 2). Для цитотоксичного вещества аллоксана C4H2O4N2 с максимально допустимым содержанием атомов кислорода у пиримидиновых таутомеров значение –2nO = –8 и n* = 1,0 (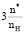 = 1,2) разность между расчетным ∆
= 1,2) разность между расчетным ∆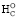 и единственным экспериментально установленным значением [31] составила 0,80 %.
и единственным экспериментально установленным значением [31] составила 0,80 %.
Заключение
В данной работе обосновывается новый методологический подход расчета значений стандартных энтальпий сгорания (∆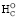 ) протеиногенных аминокислот и азотистых оснований, учитывающий различия в их элементном составе и структурной организации.
) протеиногенных аминокислот и азотистых оснований, учитывающий различия в их элементном составе и структурной организации.
Протеиногенные аминокислоты являются карбоновыми кислотами с альфа-аминогруппой –NH2, связанной через атом углерода с карбоксильной группой –COOH, отличаются друг от друга структурой боковых групп. Предложено эмпирическое уравнение прямого расчета энтальпий сгорания α-аминокислот (кДж∙моль-1):
∆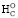 = –96,485 [4nC + 1,229nH + 6nS – ≤ 2nO],
= –96,485 [4nC + 1,229nH + 6nS – ≤ 2nO],
где учтено число Фарадея 1F = 96485 Кл× ×моль-1 (заряд электрона, помноженный на число Авогадро); число атомов в молекуле (nC, nH, nS, nO) и соответствующие им валентности; сомножитель 1,229 при nH отражает поправку на значение электродного потенциала электрохимической реакции кислород-водород (∆EO 1,229 В). Здесь сохранена форма записи основных составных частей уравнения расчета ∆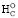 , варьирует лишь параметр ≤ –2nO (от –2nO до –0,25nO), уменьшаясь по мере усложнения строения боковых групп α-аминокислот.
, варьирует лишь параметр ≤ –2nO (от –2nO до –0,25nO), уменьшаясь по мере усложнения строения боковых групп α-аминокислот.
Главные и минорные моноциклические пиримидиновые и бициклические пуриновые основания характеризуются наличием одной C=C связи, двух атомов азота в каждом цикле в составе ковалентных одинарной C–N и двойной C=N связей, участвующих в перераспределении валентных электронов при переходе одной резонансной формы в другую. Гибридные электронные структуры придают кольцевым молекулам дополнительную стабилизирующую энергию резонанса. С другой стороны, благодаря наличию замещающих боковых карбонильных C=O и/или аминных NH2 групп природные азотистые основания существуют в виде смеси таутомерных форм. В паре таутомеров атом водорода способен переходить из одного положения в другое. В составе нуклеозидов основания существуют преимущественно в более устойчивых кето- и аминоформах. У азотистых оснований таутомерия и резонанс взаимосвязаны. Для расчета их энтальпий сгорания предложено иное эмпирическое уравнение (кДж∙моль-1):
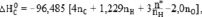
где для таутомеров с C=O группами число перемещаемых к газообразному кислороду электронов уменьшается на одинаковую величину –2nO; дополнительный параметр 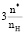 учитывает валентность атомов азота и общее количество кратных связей C=N и C=C (n*) в резонансной структуре по отношению к содержанию атомов водорода в соединении (nH). Здесь в уравнении расчета ∆
учитывает валентность атомов азота и общее количество кратных связей C=N и C=C (n*) в резонансной структуре по отношению к содержанию атомов водорода в соединении (nH). Здесь в уравнении расчета ∆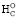 азотистых оснований нет варьирующих параметров, сохранена форма записи всех его составных частей.
азотистых оснований нет варьирующих параметров, сохранена форма записи всех его составных частей.
При изучении проблемы происхождения генетического кода при абиогенезе и начальных биогенных стадиях рассматривают комплекс связанных друг с другом физико-химических свойств, позволивших отобрать из хаотического многообразия органических соединений «первичного бульона» минимальное число протобиомономеров: 5 главных азотистых оснований, 20 протеиногенных аминокислот, несколько моносахаридов и жирных кислот [40, 41]. Ранее мною впервые было указано на температуру плавления протобиомономеров среди детерминирующих факторов их отбора при возникновении и поэтапной самоорганизации генетического кода [2]. Учитывая возможность вычисления ∆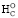 протеиногенных аминокислот и азотистых оснований по их элементному составу и структурной организации, представляется вполне оправданным предположение, что при эволюционном отборе протобиомономеров в протоклетках реализовалась и возможность биогенных элементов влиять на их структуру и физико-химические свойства.
протеиногенных аминокислот и азотистых оснований по их элементному составу и структурной организации, представляется вполне оправданным предположение, что при эволюционном отборе протобиомономеров в протоклетках реализовалась и возможность биогенных элементов влиять на их структуру и физико-химические свойства.
Работа выполнена в рамках государственного задания, регистрационный номер НИОКТРАААА-А19-11911229009-1.
Библиографическая ссылка
Саралов А.И. РАСЧЕТ ЭНТАЛЬПИЙ СГОРАНИЯ АМИНОКИСЛОТ И АЗОТИСТЫХ ОСНОВАНИЙ ПО ИХ ЭЛЕМЕНТНОМУ СОСТАВУ И СТРУКТУРЕ // Международный журнал прикладных и фундаментальных исследований. 2020. № 3. С. 113-121;URL: https://applied-research.ru/ru/article/view?id=13045 (дата обращения: 03.03.2026).
DOI: https://doi.org/10.17513/mjpfi.13045


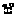
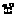 = – 96,485 [x]
= – 96,485 [x]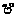 [8, 11]
[8, 11]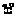 [источник]
[источник]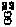
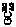
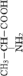
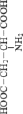
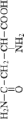
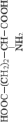
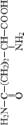
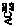
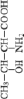
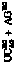
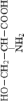
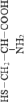
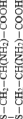
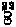
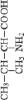
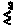
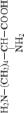
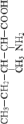
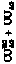
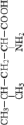
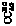
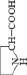
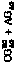
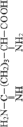
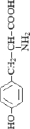
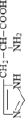
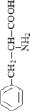
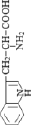
 [источник]
[источник] = – 96,485 [x]
= – 96,485 [x]