Известно, что на твердую сферическую частицу, движущуюся с переменной скоростью t в вязкой жидкости, действует сила, зависящая от предыстории движения. Британскому математику Альфреду Бассе удалось построить интегрально-дифференциальное уравнение, которому удовлетворяет скорость V(t) осаждения частицы.
При построении решения данного уравнения приходится рассматривать различные случаи, возникающие из-за различных значений плотностей жидкостей и порядков дробных производных, входящих в уравнение. Более того, решение для каждого отдельного случая представляет существенную сложность и не является удобным в применении. Это заметно по решениям, представленным в [1] и [2].
Ввиду этого возникает необходимость поиска другого подхода к поиску решения задачи. Целью данной работы является построение асимптотического ряда решения уравнения, справедливого для любых значений плотностей жидкостей и порядков дробной производной 0 < α < 1, а также сравнение полученного результата с известным точным решением.
Перед формулировкой задачи отметим, что для частных производных порядка 0 < α < 1 при нулевом начальном условии дробные производные по Капуто и Риману – Лиувиллю являются эквивалентными, то есть при y(a) = 0 и 0 < α < 1 выполняется равенство 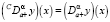 [2, с. 92–93].
[2, с. 92–93].
В рамках рассматриваемой задачи справедливы обозначенные выше условия. Поэтому при ее решении, не оговаривая дополнительно, будем подразумевать справедливость перехода от дробной производной Капуто к дробной производной по Риману – Лиувиллю.
Постановка задачи и составление модели
Рассмотрим нестационарное движение сферы, погруженной в несжимаемую вязкую жидкость, под действием гравитации. Ограничиваясь линеаризованной теорией, предполагают, что гидродинамическая наследственная сила обобщается в классическую силу Бассе по параметру 0 < α < 1. При этом, вводя в рассмотрение дробные производные, можно выразить силу Бассе через производную порядка 1/2 от скорости частицы.
Уравнение движения сферической частицы под действием силы тяжести в вязкой жидкости выражается через скалярную скорость V(t), действующую в вертикальном направлении (предполагается, что она будет положительной, если направлена вниз) по формуле [1, с. 836]
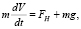 (1)
(1)
где 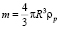 – масса частицы плотности ρp и радиуса R, g – ускорение свободного падения, FH – результирующая гидродинамических сил.
– масса частицы плотности ρp и радиуса R, g – ускорение свободного падения, FH – результирующая гидродинамических сил.
Если начальным состоянием частицы является состояние покоя в неподвижной жидкости с плотностью ρf и кинематической вязкостью v, то справедлива следующая формула [1, с. 836]
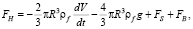
где
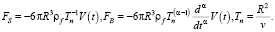
Записи FS и FB означают силы Стокса и Бассе соответственно, а выражение
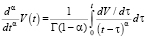
означает дробную производную 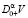 по Риману – Лиувиллю порядка 0 < α < 1 [2, с. 71].
по Риману – Лиувиллю порядка 0 < α < 1 [2, с. 71].
После подстановки составляющих результирующей гидродинамических сил и преобразований, учитывая начальное состояние покоя, уравнение (1) приводится к виду [1, с. 837; 2, с. 435]:
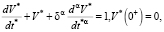 (2)
(2)
где V* и t* – безразмерные параметры скорости и времени, которые связаны с размерными переменными соотношениями
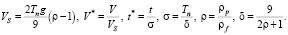 (3)
(3)
Решение модели
Для решения классического случая, рассмотренного Бассе, достаточно положить в (2) α = 1/2 и решить задачу Коши с учетом начального условия. Однако, следуя обозначенной цели, решим задачу в общем случае методом возмущений для малого положительного параметра 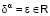 . Символ «
. Символ «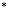 » в уравнении (2) для удобства будем опускать. Таким образом, имеем следующую систему:
» в уравнении (2) для удобства будем опускать. Таким образом, имеем следующую систему:
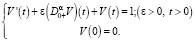 (4)
(4)
Решение первого уравнения в (4) будем искать в виде ряда по степеням ε, то есть
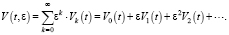
Подставляя это разложение в (4), получим
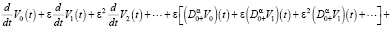
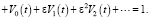 (5)
(5)
При ε = 0 решением уравнения является функция V0(t) = 1 – e-t. Подставляя найденную функцию в (5) и приравнивая коэффициенты при первой степени ε, получим
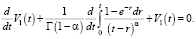 (6)
(6)
Для решения последнего уравнения предварительно преобразуем интеграл в дробной производной. Для этого введем вспомогательную функцию f(t), где
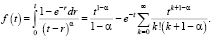
Обозначая дробную производную в (6) через b(t), получим уравнение вида 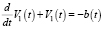 . Решая его методом вариации произвольной постоянной, получим
. Решая его методом вариации произвольной постоянной, получим
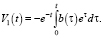
Производя обратную замену 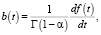 имеем
имеем
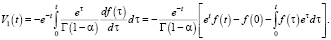
Вычисляя недостающие слагаемые в правой части полученного равенства, получаем, что f(0) = 0 и
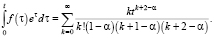
Тогда
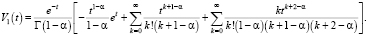
После преобразований получим
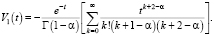 (7)
(7)
Аналогичным образом вычислим V2(t). Приравнивая коэффициенты при второй степени ε, получим уравнение
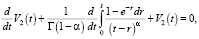
решение которого, очевидно, представимо в виде
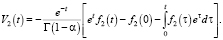 (8)
(8)
Находя слагаемые в правой части (8), получим следующие равенства
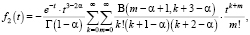
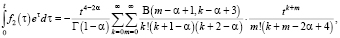
где B(x, y) – бета-функция Эйлера.
Подставляя данные выражения в (8), учитывая f2(0) = 0 и выполняя элементарные преобразования, получим равенство
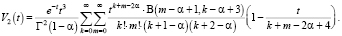 (9)
(9)
Таким образом, получаем
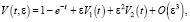 (10)
(10)
где V1(t) и V2(t) определены равенствами (7) и (9) соответственно.
Тогда асимптотический ряд для случая α= 1/2 будет иметь вид
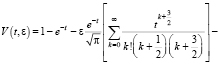
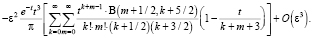 (11)
(11)
Для практических расчетов в равенствах (10) и (11) надо положить V = V* и t = t*, которые определяются формулами (3).
Сравнение с точным решением
Сравним полученный нами результат с точным решением дифференциального уравнения в (4) при α= 1/2, которое представлено в [2, с. 298]:
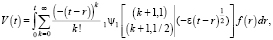
где 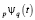 – обобщенная функция Райта, определенная, например, в [2, с. 56]. В нашем случае она имеет вид
– обобщенная функция Райта, определенная, например, в [2, с. 56]. В нашем случае она имеет вид
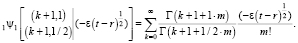
Тогда, учитывая f(r) = 1, получим
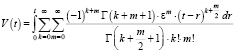
или
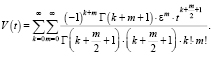 (12)
(12)
Сравнение точного решения с асимптотическим рядом при α = 1/2
|
t |
Точное решение (12) |
1 – e-t |
1 – e-t + εV1(t) |
1 – e-t + εV1(t) + ε2V2(t) |
|
1 |
0,495417 |
0,632120 |
0,458847 |
0,504832 |
|
2 |
0,677900 |
0,864664 |
0,625311 |
0,692978 |
|
3 |
0,764828 |
0,950212 |
0,719846 |
0,775856 |
|
4 |
0,812661 |
0,981684 |
0,780815 |
0,817446 |
|
5 |
0,842017 |
0,993262 |
0,821212 |
0,842268 |
|
6 |
0,861646 |
0,997521 |
0,848403 |
0,859556 |
Полагая ε = 0,5, получим следующие результаты (для вычисления значения V(t) воспользуемся базой Wolfram Alpha) (таблица).
Из таблицы видно, что увеличение числа приближений, как и ожидалось, дает более точные значения. Второе приближение даже при ε = 0,5 дает вполне удовлетворительные результаты. При уменьшении значения ε точность полученного решения возрастает.
При изменении порядка дробной производной в асимптотическом ряде (10) (ε = 0,5) наблюдается следующая зависимость (рисунок).
Из графика видно, что порядок дробной производной оказывает существенное влияние на скорость частицы, то есть эффекты вязкости подобны аномальным диффузионным явлениям, которые описываются дробными производными.
Заключение
Построенное нами асимптотическое решение справедливо для любых значений плотностей жидкостей и порядков дробной производной 0 < α < 1. Удовлетворительное совпадение результатов точного и приближенного решений позволяет использовать полученную формулу для практических расчетов. На основании этого можно утверждать, что цель работы была достигнута.
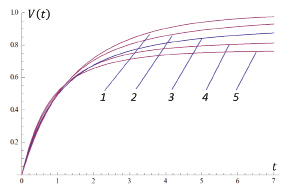
График зависимости V(t) от безразмерного параметра t при различных значениях порядка дробной производной: 1. α = 0,1, 2. α = 0,3, 3. α = 0,5, 4. α = 0,7, 5. α = 0,9
С практической важностью рассмотренной темы, анализом литературных данных и экспериментальными результатами можно ознакомиться в работах [3–6], а в работе [7] для численного моделирования нестационарных течений проводится верификация метода вязких вихревых доменов.
Автор выражает благодарность научному руководителю департамента математики и физики МГПУ В.А. Чугунову за ценные советы при написании текущей работы.
Библиографическая ссылка
Ковалев М.Д. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ТЕЛА В НЕСЖИМАЕМОЙ ЖИДКОСТИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ ДРОБНОГО ПОРЯДКА // Международный журнал прикладных и фундаментальных исследований. 2020. № 11. С. 51-56;URL: https://applied-research.ru/ru/article/view?id=13148 (дата обращения: 03.03.2026).
DOI: https://doi.org/10.17513/mjpfi.13148

