Постоянным актуальным требованием к организации производственной деятельности предприятий любой формы собственности, является их устойчивость, зависящая в первую очередь от способности эффективно распоряжаться (управлять) имеющимися ресурсами.
Для предприятия городского пассажирского транспорта, такого как Петербургский метрополитен, ежедневно удовлетворяющего потребность пассажиров в перемещении из одной части города в другую, основным ресурсом, от которого зависит его эффективность, является определяющее объем перевозимого пассажиропотока [1] техническое состояние эксплуатируемого парка техники, в том числе эскалаторного хозяйства.
Вместе с тем техническое состояние парка техники – переменная, на которую в каждый момент времени оказывает влияние множество внутренних и внешних факторов, взаимосвязь и результирующий эффект которых описывается вероятностными зависимостями.
При принятии стратегических и тактических управленческих решений [2–4] по поддержанию технического состояния на достаточном уровне в условиях неопределенности, формируется необходимость извлекать максимум информации из имеющихся потоков, циркулирующих от элементов подсистем к оператору и обратно, описанных в работе [5], а также руководствоваться результатами построения прогноза.
Однако согласно работам [6–8] на сегодняшний день существует многообразие подходов к построению прогноза технического состояния, которые необходимо адаптировать к конкретным условиям применения.
Объектом исследования в данной работе выступает эскалаторное хозяйство метрополитена, а предметом – прогноз технического состояния.
Цель данной работы – определить алгоритм, который упорядочивает совокупность операций и адаптирует их для разработки прогноза технического состояния эскалаторов.
В качестве научной новизны выступает целенаправленное использование комбинации известных моделей и методов, включая нейронные сети, в приложении к построению прогноза технического состояния тоннельных эскалаторов метрополитена.
Определение последовательности построения прогноза технического состояния
Первоначально выполняется преобразование информационных потоков, содержащих большой объем структурированных и неструктурированных данных [9] об объектах эскалаторного хозяйства и связанных с ним объектов инфраструктуры. Преобразование этих потоков осуществляется через сбор исходной информации и ее представление в специальном виде посредством использования комплексного электронного документа – наряда-допуска, структура которого представлена в работе [10].
В результате выполненного преобразования формируется возможность извлекать из электронного документа причинно-следственную информацию, которая в дальнейшем используется нейронной сетью прямого распространения для распознавания подобия и различия, а также обобщения входных данных, в том числе по отношению к ранее не встречавшимся.
Иными словами, при поступлении на вход нейронной сети исходных данных, включающих в том числе параметрические, полученные от контрольно-измерительного оборудования, являющиеся компонентами вектора причин X входного вектора ситуаций {Si},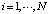 
при сохранении определенной части исходных признаков причин, не происходит изменение реакции Yt+1 нейронной сети на исходные следствия, и в зависимости от того, с каким из выделенных подмножеств сеть нашла наибольшее совпадение, формируются следующие рекомендации:
1. Элемент подсистемы эскалатора находится в работоспособном состоянии. Негативная динамика изменения технического состояния отсутствует. Нет потребности в корректирующем воздействии.
2. Элемент подсистемы эскалатора находится в работоспособном состоянии. Негативная динамика изменения технического состояния присутствует. Есть потребность в корректирующем воздействии.
3. Элемент подсистемы эскалатора находится в работоспособном состоянии. Негативная динамика изменения технического состояния присутствует. Нет потребности в корректирующем воздействии.
4. Элемент подсистемы эскалатора находится в неработоспособном состоянии. Негативная динамика изменения технического состояния отсутствует. Есть потребность в корректирующем воздействии.
5. Элемент подсистемы эскалатора находится в неработоспособном состоянии. Негативная динамика изменения технического состояния присутствует. Есть потребность в корректирующем воздействии.
6. Нет полного совпадения поступивших исходных данных ни с одним электронным документом в информационном пространстве. Установлено частичное совпадение исходных данных с рядом электронных документов, хранящихся в информационном пространстве. Формируется ранжированный перечень совпадений, из которого отбирается наиболее подходящий. Есть потребность в корректирующем воздействии. Создается новый электронный документ.
7. Нет полного совпадения поступивших исходных данных ни с одним электронным документом в информационном пространстве. Установлено частичное совпадение исходных данных с рядом документов, хранящихся в информационном пространстве. Формируется ранжированный перечень совпадений, из которого отбирается наиболее подходящий. Нет потребности в корректирующем воздействии. Создается новый электронный документ.
8. Нет полного совпадения поступивших исходных данных ни с одним электронным документом в информационном пространстве. Не установлено частичное совпадение исходных данных ни с одним электронным документом в информационном пространстве. Нет потребности в корректирующем воздействии. Создается новый электронный документ.
9. Нет полного совпадения поступивших исходных данных ни с одним электронным документом в информационном пространстве. Не установлено частичное совпадение исходных данных ни с одним электронным документом, хранящимся в информационном пространстве. Есть потребность в корректирующем воздействии. Создается новый электронный документ.
Реализация вышеописанного механизма получения рекомендаций на основе множества данных о состоянии элементов подсистем эскалатора и сопутствующей информации, хранящейся в информационном пространстве, осуществляется за счёт выделения подмножества идентификационных признаков причин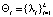 
(при фиксированном объеме N обучающей выборки Ω1 (части библиотеки нарядов-допусков), которые являются общими и для вновь поступающей информации, среди которой также присутствует множество причин X, способствующих формированию следствий 
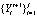определяющих техническое состояние элементов подсистем эскалатора. В качестве признаков предлагается использовать компоненты векторов из нарядов-допусков и библиотек, такие как код классификатор, вид работ и т.д.
Общий принцип обучения нейронных сетей [11], заключается в увеличении весов для двух одновременно активных нейронов, который формализован выражением
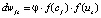, (1)
где dwjs – величина изменения синапса wjs; cj и us – уровни возбуждения ј-го и s-го нейронов; f – преобразующая функция; φ – константа, определяющая скорость обучения.
При условии полносвязной структуры сети увеличение числа активных нейронов компенсируется равным уменьшением пассивных нейронов. Веса wjs элементов нейронной сети, обрабатывающих подмножество выделенных признаков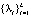 
причин, присутствующих во всех подобных входных множествах причин X, будут многократно поощрены.
Перераспределение весов в нейронной сети выполняется при формировании наряда-допуска. Заполненные идентификационные характеристики наряда-допуска соотносятся с выделенными подмножествами дополнительных признаков λl причин Xi,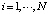 
нарядов-допусков, хранящихся в библиотеках, при этом наблюдается усиление синоптических связей нейронов, связанных с обработкой конкретного признака.
В результате обучения нейронной сети на фиксированном объеме N обучающей выборки Ω1 (части библиотеки нарядов-допусков) образуется гиперповерхность A, отражающая состояние элементов подсистем эскалатора и рекомендации, принятые за «эталонные». В процессе использования «эталонных» рекомендаций при реальной эксплуатации, образуется гиперповерхность B и набор дополнительных параметров E:
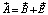, (2)
где E – дополнение параметров гиперповерхности B до «эталонной» A.
Получившаяся гиперповерхность B описывается моделью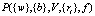 
:
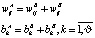, (3)
где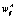 
– значение весового коэффициента между i-м и ј-м нейронами соседних слоев при обучении на выборке Ω1; 
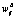– значение весового коэффициента по результатам обучения нейронной сети при реальной эксплуатации, 
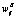– дополнение 
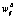до истинного 
.
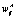Параметры w и b примем статистически усредненными по обучающей выборке, поэтому выражение (2) запишем в виде
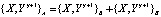, (4)
где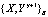 
– входная и выходная последовательности обучающей выборки за период 
.
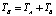Выражения (2)–(4) показывают, что дополнение E гиперповерхности A зависит от величин приращений элементов нейронной сети, выполняющих функцию запоминания информации. Эффект доопределения гиперповерхности B до «эталонной» A получается подбором признаков (подмножеств) входных причин X и сопоставим с увеличением времени наблюдения технического состояния элементов подсистем эскалатора.
В процессе работы алгоритм соотносит поступившие текущие значения параметров с ближайшим параметром из подмножества, хранящегося в информационном пространстве.
Для сопоставления новой информации и информации, хранящейся в информационном пространстве, при условии евклидовой метрики (евклидова расстояния) обоих информационных массивов показатель сходства определяется по формуле расстояния Хэмминга:
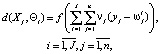(5)
где f – функция расстояния между данными; J – количество классов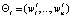 
, прогнозируемых следствий 
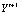; n – количество признаков вектора Y технического состояния элементов подсистем эскалатора; vj – коэффициент значимости ј-го выделенного признака.
Данное расстояние является разностью по координатам многомерного пространства и идентично евклидовому. Преимуществом расстояния Хэмминга является малая чувствительность к выбросам (отдельным большим разностям), что обеспечивается отсутствием возведения в квадрат.
В случае если признак yj = λj находится на пересечении признакового пространства двух образов YA и YB и коэффициент vj его значимости превышает определенную величину суммарной значимости остальных, то оба образа будут неразличимы:
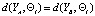. (6)
Поэтому для повышения качества распознавания следствий Y и преодоления недостатка априорной информации вводится ассоциативный признак (группы ассоциативных признаков) в исходное множество признаков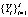 
, ускоряющих формирование прогнозной модели P.
Ассоциативный признак ρ – коэффициент подобия, отражает степень проявления эффекта обобщения или различия с бинарной функцией выхода:
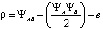, (7)
где ΨAB – доля элементов нейронной сети, реагирующих как на признаки причин, хранящиеся в информационном пространстве XA, так и на вновь поступившие XB; ΨA – доля элементов нейронной сети, реагирующих на признаки XA; ΨB – доля элементов нейронной сети, реагирующих на признаки XB; e > 0 – компонента потерь.
Функция Ψ – это соотношение значений входных признаков и хранящихся в информационном пространстве, определяется выражением
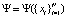. (8)
Коэффициент подобия ρ < 0 в случае, когда вектор ΨA не подобен ΨB, а также (пренебрегая компонентой e) при равнозначности признаков входных данных и одинаковом объеме суммарных величин поощрений полученных нейронной сетью в результате многократного появления подобных данных.
В результате обучения нейронной сети коэффициент подобия принимает значения больше нуля и любая входная информация, содержащая признак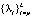 
, активирует ΨAB часть сети.
После определения основных принципов, используемых для построения прогноза, перейдем к конкретизации нейросетевой модели через определение ее параметров, таких как число слоев, число нейронов в каждом слое и функцию активизации нейронов.
Для этого используем одну из известных архитектур – полносвязную сеть прямого распределения с двумя промежуточными слоями, представленную на рис. 1 и описанную выражением (9). Предложенная нейронная сеть выполняет разделение на классы множества признаков выпуклыми гиперплоскостями и обобщение по преобладанию (сходству).
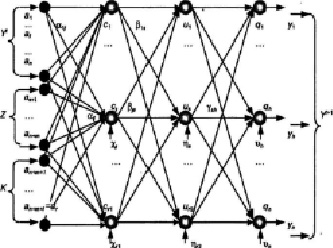
Рис. 1. Архитектура прогнозирующей НС
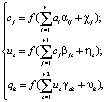(9)
где ai – значение i-й компоненты причинной составляющей X ситуации наряда-допуска, 
. Элементы ai,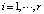 
описывают распределительный слой нейронной сети; cj – значение выхода ј-го нейрона первого скрытого слоя нейронной сети, 
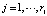; us – значение выхода s-гo нейрона второго скрытого слоя нейронной сети, 
; 
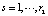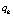– значение выхода h-го нейрона выходного слоя нейронной сети, 
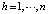; f – функция активизации нейрона; α, β, γ – коэффициенты синаптических связей; χ, η, υ – смещения нейронов первого и второго скрытых и выходного слоев; r – размерность входного вектора (задачи прогнозирования), это количество параметров ситуации из наряда-допуска; 
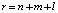, n – количество параметров технического состояния элементов подсистем эскалатора; m – количество факторов прогнозного фона; l – количество управляющих воздействий/индекс переменных, характеризующих режимы функционирования эскалатора.
Модель, описанная выше, осуществляет обобщение по подобию, формируя изолированные области на множестве компонентов (признаков) входных векторов причин (исходных данных) за счёт работы первого промежуточного слоя. Ограничение прогностической способности сети зависит только от количества нейронов. Однако при увеличении числа скрытых слоев более двух происходит увеличение трудоемкости обучения.
Для исключения нарушения работы нейронной сети из-за чрезмерного увеличения весовых коэффициентов синаптических связей используется сигмоидная функция активизации нейронов, которая асимптотически приближается к предельным значениям, никогда не достигая их (рис. 2). Функция активизации (передаточная функция) нейронов определяет выходное значение сигнала относительно входного в зависимости от результата работы сумматора и порогового значения.
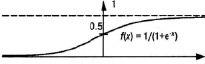
Рис. 2. Сигмоидная функция активизации нейрона
Далее подберем значения весов α, β, γ и величин смещения χ, η, υ, обеспечивая наименьшее значение показателя Ф при подаче на вход вектора причин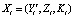 
:
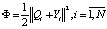(10)
где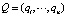 
– вектор выходных данных; N – число ситуаций, характеризующих текущее техническое состояние элементов эскалатора.
В случае евклидовой нормы выражение (10) записывается в виде
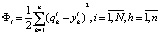, (11)
где n – размерность вектора параметров технического состояния элементов подсистем эскалатора.
Для оптимизации механизма подбора введем критерий формирования параметров прогнозной модели:
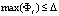, (12)
где Δ – предел относительной погрешности H восстановления ситуации Si,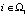 
, 
.
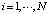Используя метод градиентного спуска (градиентный метод поиска) для минимизации функции Ф получим производные по модифицируемым параметрам прогнозирующей двухслойной нейронной сети (рис. 1):
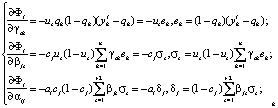(13)
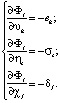(14)
В результате имеем ошибки восстановления прецедентов eh, σs, δj нейронов выходного, скрытых первого и второго слоев, которые в дальнейшем используются для вычисления градиентов, в последующем применяемых для изменения множества весовых коэффициентов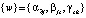 
и множества 
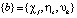величин смещения нейронов.
Для первичной настройки сети для задания множества весовых коэффициентов и множества величин смещений используем следующую последовательность шагов:
а) задание множеств весовых коэффициентов {w} и величин смещения {b} случайными числами в диапазоне ([0,1] или [-1,1]);
б) активизация нейронов входного слоя нейронной сети вектором причин {Xi},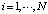 
для каждой ситуации наряда-допуска
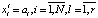; (15)
в) расчет выходных величин нейронов выходного слоя qh,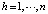 
в соответствии с системой уравнений (9);
г) вычисление ошибки между полученными на предыдущем этапе выходными величинами нейронов qh и компонентами yh выходного вектора следствий Yt+1 обучающей выборки Ω1 (библиотек нарядов-допусков) с последующим пересчетом величины ошибки для всех нейронов двух нижележащих слоев согласно выражениям
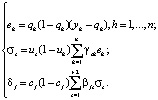(16)
д) перерасчёт весовых коэффициентов и пороговых величин (метод градиентного спуска):
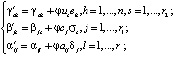(17)
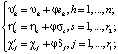(18)
где φ > 0 – скорость обучения нейронной сети, определяемая экспериментальным путем;
е) в соответствии с (19) вычисление максимальной относительной погрешности восстановления h-й компоненты yh вектора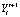 
, 
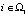параметров технического состояния элементов подсистем эскалатора:
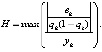(19)
Сравнение ошибок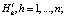 
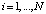для всех N примеров {Si}, 
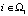обучающей выборки Ω1. При 
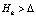переход к шагу б) настоящего алгоритма. В случае 
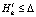нейронной сети считается обученной, а параметры и структура прогнозной модели определенными.
Для обучения нейронной сети по текущим данным, включая измеренные параметры элементов эскалатора, выберем алгоритм Левенберга – Марквардта, обеспечивающий большую скорость обучения (сходимости) относительно метода обратного распространения ошибки (градиентного спуска).
Данный алгоритм оптимизирует параметры (18) нейронной сети по критерию среднеквадратической ошибки. Работа алгоритма заключается в последовательном приближении заданных начальных значений параметров нейронной сети к искомому локальному оптимуму.
Алгоритм Левенберга – Марквардта отличается от метода градиентного спуска тем, что использует матрицу Якоби, а не градиент вектора параметров, а от алгоритма Гаусса-Ньютона тем, что использует параметр регуляризации. Взаимная зависимость алгоритмов приведена на рис. 3 и в таблице. Визуализация свойств, приведенных в таблице, изображена на рис. 4.
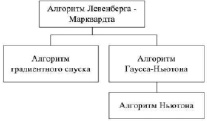
Рис. 3. Зависимость алгоритмов
Сравнительный анализ методов
|
Алгоритм градиентного спуска |
Алгоритм Ньютона |
Алгоритм Ньютона – Гаусса |
Алгоритм Левенберга –Марквардта |
|
|
Целевая функция |
дифференцируемая |
дважды дифференцируемая |
нелинейный метод наименьших квадратов |
нелинейный метод наименьших квадратов |
|
Достоинства |
– простота реализации; – низкая ресурсоемкость |
– высокая скорость сходимости вблизи экстремума; – использует информацию о кривизне пространства |
– очень высокая скорость сходимости; – хорошо работает с задачей линейной аппроксимации |
– наибольшая устойчивость среди рассмотренных методов; – хорошо работает с задачей линейной аппроксимации; – очень высокая скорость адаптивной сходимости; – высокая вероятность найти глобальный экстремум |
|
Недостатки |
– сложный поиск глобального минимума; – низкая скорость сходимости вблизи экстремума |
– функция должна быть дважды дифференцируема; – высокая вероятность не найти локальный экстремум; – большая ошибка, при условии вырожденности матрица Гессе (отсутствие обратной) |
– линейная независимость столбцов матрицы Якоби; – отсутствуют ограничения на вид целевой функции |
– линейная независимость столбцов матрицы Якоби; – отсутствуют ограничения на вид целевой функции; – сложность реализации |
|
Сходимость |
локальная |
локальная |
локальная |
локальная |
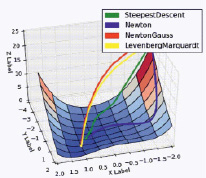
Рис. 4. Совмещённый результат работы алгоритмов
В ходе реализации данного алгоритма (в частности, при вычислении показателя Ф, подобного показателю (10)) не осуществляется вычисление матрицы Гессе:
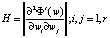, (20)
требующее больших объемов памяти ЭВМ для обучения сети.
Вместо этого матрица Гессе аппрокси- мируется:
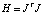, (21)
и градиент/величина коррекции весовых коэффициентов и величин смещения нейронов (выражения (13), (14)) вычисляется как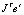 
. Где J – определитель Якоби из частных производных первого порядка ошибок весовых коэффициентов и смещений, а e' – вектор ошибки между вычисленными выходными величинами нейронов qh и компонентами yh выходного вектора следствий Yt+1 обучающей выборки.
Вычисление определителя Якоби
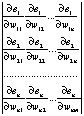(22)
требует гораздо меньше ресурсов по сравнению с использованием матрицы Гессе при вычислении вторых производных функции ошибки.
Выражение, описывающее модификацию весовых коэффициентов сети, выглядит как
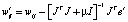, (23)
где μ – скалярная величина; I – единичная матрица.
В случае μ = 0 это метод Ньютона, где матрица Гессе аппроксимируется на каждой итерации с использованием градиента. В случае μ >> 0 коррекция весов и величин смещения нейронов пропорциональна производным сетевой ошибки по этим весам и смещениям, за счет чего выполняется минимизация общей сетевой ошибки.
Алгоритм обучения Левенберга – Марквардта использует для поиска оптимума показатель (10) или сочетание линейной аппроксимации и градиентного спуска (11) в зависимости от успешности линейной аппроксимации.
После выбора архитектуры нейронной сети и способов ее обучения, опишем механизм получения прогноза.
Для получения прогноза технического состояния элементов эскалатора на входной слой ai обученной нейронной сети подается вектор причин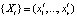 
реальной выборки, не равной обучающей 
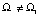. В результате чего формируется отклик нейронной сети в выходном слое qh, характеризующий прогнозную оценку будущего вектора следствий Yt+1 параметров технического состояния элементов подсистем эскалатора. Здесь 
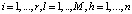. Однако поведение контролируемых параметров элементов подсистем эскалатора в каждый момент времени случайно, поэтому результат настройки весовых коэффициентов и величин смещения нейронной сети имеет вероятностный смысл. Поэтому для параметров yh технического состояния элементов подсистем эскалатора примем, что компоненту yh вектора 
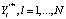соответствует условная плотность вероятности, описываемая нормальным законом распределения:
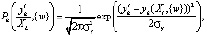
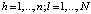, (24)
где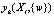 
– функция, значение которой в точке Xl соответствует математическому ожиданию случайной величины 
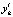; σy – среднее квадратичное отклонение случайной величины 
.
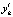Следовательно, результатом функционирования прогнозирующей нейронной сети можно считать вычисленный нейронной сетью вектор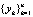 
параметров технического состояния, компоненты которого являются результатом статистического усреднения по всей обучающей выборке.
Полученный результат прогнозирования верифицируется через оценку достоверности/точности и проверку обоснованности прогноза, с учётом качества используемой исходной информации. Под верификацией прогноза и прогнозной модели P, синтезированной по данным обучающей выборки Ω1 (части библиотеки нарядов-допусков), будем понимать интегрированную оценку достоверности по проверочной выборке Ω2 ≠ Ω1.
В соответствии с критерием (19) все данные, структурированные электронным документом, разбиваются на обучающую выборку Ω1 для синтеза параметров прогнозной модели и проверочную выборку Ω2 для ее верификации.
В случае если условие (19) выполняется, задача синтеза прогнозной модели принимается решенной, иначе последовательность операций выполняется заново.
Результаты исследования и их обсуждение
Вышеописанная последовательность действий (операций) формирует алгоритм прогнозирования, поиск которого и был целью данной работы.
Таким образом, прогнозирование технического состояния элементов эскалатора включает: сбор исходных данных и их адаптацию; выбор (построение) прогнозирующей архитектуры нейронной сети и ее параметров; выбор (построение) прогнозной модели; получение прогноза; верификация прогнозной модели и результатов ее работы.
Заключение
Описанный выше алгоритм прогнозирования скомпилирован с учетом недостатка исходных данных, интеллектуализации управления ресурсами и имеющихся возможностей качественной и количественной оценки выходных данных. В качестве одного из преимуществ применения алгоритма является возможность его реализации стандартными инструментами ряда специализированных многофункциональных программных платформ и созданных на их основе программных комплексов и компонентов [12].
Вместе с тем за счёт возможности выбора метода прогнозирования и использования нечеткой логики, алгоритм способен адаптироваться к конкретной исходной информации, поступившей после анализа конкретной ситуации.
При построении прогноза технического состояния, для каждой ситуации (в том числе технического воздействия), описанной электронным документом, входными ограничениями являются объем ресурсов, включая финансовые, отклонение от срока и качества работ, а одним из выходных ограничений – оценка эффективности выполненных работ, при этом каждое из ограничений может иметь нечеткие отображения.
Также предложенный алгоритм является одним из инструментов, который возможно использовать в информационном пространстве, предназначенном для обеспечения доступа к хранилищам знаний, формирования различных отчетов/справок/таблиц/матриц/журналов, а также сокращения времени обработки и предоставления информации. Однако внедрение информационного пространства с интегрированным в него прогностическим компонентом в существующие организационные связи между подразделениями сопряжено с появлением следующих компонентов:
– Баз данных (знаний) по всем направлениям управления ресурсами.
Использование баз данных обеспечивает раздельный учет ресурсов и их совместный анализ при отслеживании показателей бюджетного баланса для прогнозирования возможных вариантов отклонения от заданных технических и экономических показателей.
– Комплексной (комплексированной) информации.
Обобщение аккумулируемой информации о техническом состоянии эскалаторного парка осуществляется через создание объектно-элементной модели эскалаторного хозяйства, построенной по результатам обработки электронных документов, описывающих свойства, особенности динамики и взаимосвязи с факторами внешней и внутренней среды, а также совокупностью гипотез о свойствах каждого из более 300 эскалаторов. Собранная таким образом информация о характеристиках парка формализуется в том числе через словесно-описательные модели, которые уточняются в процессе обучения нейронной сети.
– Признакового пространства
Для повышения качества построения прогноза технического состояния используется признаковое пространство, выделяемое при анализе электронных документов, хранящихся в информационном пространстве, содержащем формализованную модель эскалаторного хозяйства.
– Эталонных объектов
В связи с тем, что невозможно учесть множество факторов, определяющих динамику эксплуатационных процессов и погрешности измерений, при обучении нейронной сети возникает несоответствие модели и реального объекта (процесса), которое не должно превышать установленных отклонений. При этом величина допустимых отклонений определяется объемом обучающей выборки, а показатели точности модели характеризуются степенью приближения моделируемых данных к фактическим наблюдениям. Для приведения реальных объектов эскалаторного хозяйства и связанных с ними объектов инфраструктуры к эталонным применяется ряд переводных коэффициентов, при этом выполняется сравнение построенной модели и характеристик и свойств реального объекта. По результатам сравнения осуществляется уточнение прогнозной модели.
– Древовидной структуры построения прогноза.
В силу вероятностного характера достаточно достоверным прогноз будет, если в периоде упреждения, конфигурация причинно-следственных связей объектно-элементной структуры эскалаторного хозяйства будет идентичной или близкой к той, которая была на этапе обучения, что достаточно сложно реализуемо. Для упрощения построения прогноза предлагается выполнять частные прогнозы на каждом из уровней древовидной иерархии эскалаторной службы, используя для построения прогноза на следующем уровне только полученные результаты, не транслируя служебную информацию. Таким образом, прогноз технического состояния всего эскалаторного парка будет сводиться к обобщённому прогнозу от нескольких структурных подразделений.
Созданное с учётом вышеописанных компонентов и моделей/алгоритмов прогнозирования, информационное пространство обеспечивает выработку рекомендаций, способствующих повышению эффективности и безопасности эксплуатации эскалаторного хозяйства метрополитена.
Библиографическая ссылка
Еланцев В.В. К ВОПРОСУ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ И БЕЗОПАСНОСТИ ЭКСПЛУАТАЦИИ ТОННЕЛЬНЫХ ЭСКАЛАТОРОВ МЕТРОПОЛИТЕНА. АЛГОРИТМ ПРОГНОЗИРОВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ // Международный журнал прикладных и фундаментальных исследований. – 2021. – № 2. – С. 32-41;URL: https://applied-research.ru/ru/article/view?id=13178 (дата обращения: 21.11.2024).