Простое приближенное соотношение Ломана для кодирования фазы и его недостатки
Исторически одним из первых и уже классическим методом синтеза цифровых голограмм является оригинальный метод, разработанный Ломаном и его сотрудниками [1–3].
Сущность метода Ломана заключается в следующем. Пусть голографируемый двумерный объект описывается финитной функцией u(x, y) с областью, не выходящей за пределы прямоугольника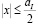 
, 
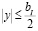, где aI и bI – пространственные размеры объекта. В плоскости синтезируемой голограммы вводятся пространственно-частотные координаты ξ и η, которые с ее пространственными координатами xH, yH связаны соотношениями
, 
,
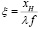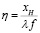где λ – длина световой волны лазерного излучения, используемого при восстановлении голограммы; f – фокусное расстояние используемой при этом Фурье-преобразующей линзы. Затем с помощью компьютера вычисляются значения отсчетов Фурье–образа
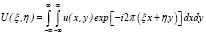
голографируемого объекта u(x, y) в узлах регулярной сеточной области, покрывающей ограниченную область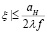 
, 
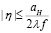плоскости голограммы ξη, где aH и bH – пространственные размеры голограммы. Шаги сеточной области Δξ и Δη выбираются в соответствии с требованиями теоремы отсчетов, т.е. 
, 
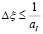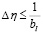. Число точек отсчета вдоль осей ξ и η равно n и m соответственно.
Затем каждый отсчёт Unm = U(nΔξ, mΔη), выбранный в узле (nΔξ, mΔη), с помощью устройств отображения компьютера кодируется в виде прозрачной прямоугольной апертуры на непрозрачном фоне. При этом cΔξ – ширина апертуры (в пространственных частотах) постоянна для данной голограммы, высота же WnmΔη с некоторым приближением прямо пропорциональна значению амплитуды Anm = |Unm| = U(nΔξ, mΔη). Смещение апертуры PnmΔξ в направлении одной из пространственно-частотных осей (скажем, в направлении оси ξ) относительно точки отсчета (nΔξ, mΔη) пропорциональна фазе φnm = arg Unm.
А именно
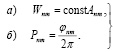(1)
Каждая такая апертура располагается в пределах прямоугольника со сторонами Δξ и Δη и геометрическим центром в узле сеточной области (рис. 1). Этот прямоугольник с апертурой называют элементарной ячейкой голограммы.
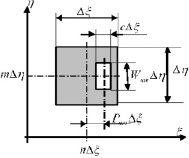
Рис. 1. Элементарная ячейка голограммы
Таким образом, синтезированная по методу Ломана голограмма представляет собой матрицу таких элементарных ячеек.
Функция пропускания голограммы, синтезированной изложенным выше способом, является бинарной и имеет вид
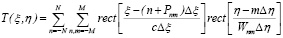, (2)
где rect(x) – прямоугольная функция, определяемая как
;
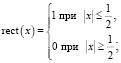
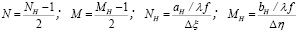NH × MH – объем выборки.
Для восстановления изображения эта голограмма помещается в плоскости P2 в оптической системе, приведенной на рис. 2, и освещается восстанавливающей плоской внеосевой световой волной R(ξ,η), которая может быть образована, в частности, точечным источником света (с амплитудой А = 1), расположенным в точке (x0, 0) плоскости P1. Тогда восстанавливающая световая волна в плоскости P2 имеет следующее распределение комплексной амплитуды [4–6]
R(ξ,η) = exp(i2πx0ξ), (3)
При этом в плоскости P3 восстановим изображение, описываемое выражением
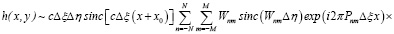
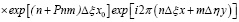, (4)
где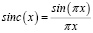 
.
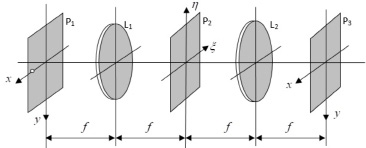
Рис. 2. Оптическая система восстановления изображения с голограммы Ломана
Дискретность и бинарность структуры голограммы является причинами появления дифракционных порядков. Если восстанавливающая световая волна R наклонена к плоскости P1 так, чтобы ее фазовый набег на Δξ составлял величину, кратную 2π (это имеет место при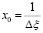 
), то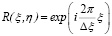 
и восстановленное изображение исходного объекта будет наблюдаться в области 
, 
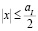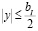. Поэтому наибольший интерес представляет лишь та часть восстановленного изображения, которая ограничена этой областью. Она описывается функцией
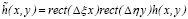. (5)
Соответствующая пространственно-ограниченная дискретная идеальная голограмма в указанной выше области восстанавливает изображение, которое запишется в виде
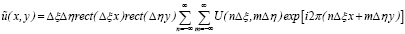. (6)
Синтезируемая голограмма будет обладать необходимыми свойствами, если (5) и (6) будут совпадать с точностью до постоянного множителя:
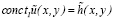. (7)
Очевидно, что в общем случае для произвольного вида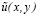 
никаким выбором параметров Pnm и Pnm не удается добиться тождественного совпадения изображений в требуемой области. Поэтому Ломан и Парис заключили, что если в интересующей нас области 
, 
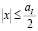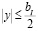, множител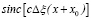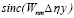и 
, 
и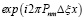 
в (4) изменяются незначительно, то, аппроксимируя их константами
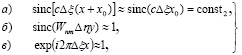(8)
можем потребовать выполнения условия (7) в виде
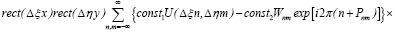
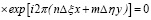. (9)
Если учесть, что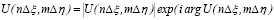 
, то из условия (9) следуют простые приближенные соотношения для вычисления параметров кодирования [7–9]:
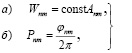(10)
где 
, 
, 
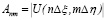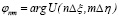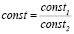(11)
Рассмотрим третье приближение (8, в) допущения (8). Его последствие приводит к искажению, вызванному наличием ошибки фазы в апертуре. Фазовая ошибка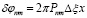 
, возникающая из-за допущения (8, в), может оказать более сильное влияние на качество изображения, чем амплитудная погрешность, возникающая из-за допущений (8, а) и (8, б) [10].
В связи с этим возникает необходимость модернизации метода, которая могла бы полностью устранить или уменьшить эту фазовую ошибку, что и является целью настоящего исследования.
Метод действительной фазы и задача уточнения фазового сдвига
Из всего вышеизложенного следует, что необходимы меры по уменьшению фазовой ошибки. Источником фазовой ошибки является смещение (сдвиг) апертуры в Фурье-плоскости относительно точки отсчета, вследствие чего фаза дифрагированной волны при восстановлении изображения равна фазе Фурье-образа в точке отсчета, а не реальной фазе, приходящейся на апертуру. То есть свет, проходящий через апертуру, расположенную в точке с координатами (nΔξ + PnmΔξ, mΔη), несет информацию, содержащуюся в точке с координатами (nΔξ, mΔη).
Поэтому в работе [3] её авторы из эвристических соображений считают, что вышеуказанная фазовая ошибка может быть устранена, если каждую апертуру располагать так, чтобы ее положение соответствовало значению фазы Фурье-образа в данной точке, а не значению фазы в точке отсчета. В этом случае параметр Pnm следует находить из решения уравнения
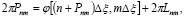(12)
где Lnm – некоторое целое число.
Подобный способ кодирования назван методом действительной (или верной, реальной) фазы.
Кодирование фазы осуществляется с помощью простого кодирующего соотношения (10, б) и уравнения (12). Для обозначения зависимости главного значения аргумента (приведенного к интервалу [–π, π]) Фурье-образа U(ξ, mΔη) от относительной (приведенной) абсциссы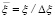 
, введена функция
ФU(ξ / Δξ)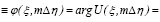
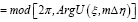, (13)
а для обозначения зависимости главного значения аргумента восстанавливающей волны R(ξ, mΔη)введена функция
ФR(ξ / Δξ)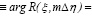 
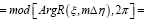
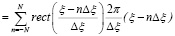, (14)
где mod[ψ, 2π] означает значение угла ψ по модулю 2π. Следовательно, они являются разрывными функциями с точками разрыва первого рода.
Компьютерное моделирование и его результаты
Прежде всего, кратко изложим алгоритм уточнения фазы. Он основан на разбиении в пределах каждой ячейки (n,m) интервал [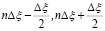
] на Kинт участков точками 
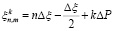, где k = 0,1,2,…,Kинт; ΔP = Δξ / Kинт и решении уравнения (12) с аппроксимацией функции 
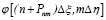кусочно-линейной функцией
,
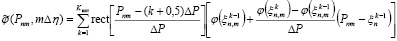где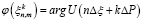 
, и последующим решением линейного уравнения, корнем которого графически является абсцисса точки пересечения аппроксимирующей прямой 
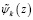и прямой 
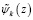, где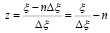
.
1. При проведении экспериментов на построенной компьютерной модели в качестве исходного голографируемого объекта была выбрана фотография, приведенная на рис. 3.
Рис. 3. Исходное изображение
2. Качество восстановленного изображения оценивалось среднеквадратическим отклонением (СКО) восстановленного изображения от исходного голографируемого объекта по формуле
,
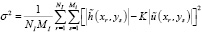где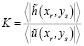 
, 
, 
,
, 
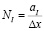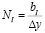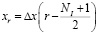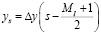
Δx, Δy – шаги дискретизации исходного объекта;
3. Для выяснения зависимости качества восстановленного изображения σ2 от степени уточнения Kинт были вычислены значения среднеквадратического отклонения σ2 для различных значений Kинт, по которым получена кривая, приведенная на рис. 4, а. Из этого рисунка видно, что оптимальное значение Kинт лежит в пределах от 4 до 8.
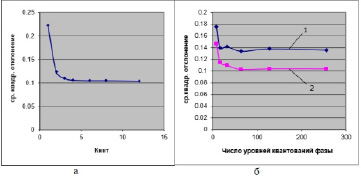
Рис. 4. Зависимости качества восстановленного изображения от: а – среднеквадратического отклонения σ2 для различных значений Kинт; б – числа уровней квантования фазы
Рис. 5. а – изображение, восстановленное с голограммы, синтезированной методом действительных фаз; б – изображение, восстановленное с голограммы, синтезированной простым методом Ломана
4. По результатам моделирования получены кривые зависимостей качества восстановленного изображения от числа уровней квантования фазы для случаев простого метода и метода действительной фазы. Они приведены на рис. 4, б (кривая 1 соответствует случаю простого метода, а кривая 2 – случаю действительной фазы). Из сравнения кривых 1 и 2 следует: уточнение фазового действительно дает положительный эффект с точки зрения минимума среднеквадратического отклонения; оптимальное значение числа уровней квантования лежит в пределах от 48 до 100.
5. Получены картины восстановленных изображений для случаев действительной фазы (рис. 5, а) и простого метода Ломана (рис. 5, б). Эти рисунки представлены в трехкратном уменьшении, так как при восстановлении голограмм происходит мультипликация изображений, что приводит к сильному увеличению размера рисунка.
Заключение
Наиболее эффективным способом решения поставленной задачи является компьютерное моделирование процессов синтеза и восстановления цифровых голограмм. Для этого, прежде всего, были выполнены следующие действия:
1. Разработан алгоритм расчета голограммы Ломана с использованием простых кодирующих соотношений (1).
2. Разработан эффективный алгоритм уточнения фазового сдвига (т.е. численного решения уравнения (12)), такой, что построенная на его основе компьютерная программа требует меньше оперативной памяти и объёма вычислений.
3. На основе результатов двух предыдущих пунктов была построена компьютерная модель процессов синтеза и восстановления голограмм, как простым методом Ломана, так и методом действительной фазы. Полученная модель позволила провести необходимые исследования.
Библиографическая ссылка
Тультемирова Г.У., Шаршеева К.Т., Аккозов А.Д., Алымкулов С.А., Исманов Ю.Х., Жумалиев К.М. УТОЧНЕНИЕ ФАЗОВОГО СДВИГА ПРИ СИНТЕЗЕ ГОЛОГРАММ МЕТОДОМ ЛОМАНА // Международный журнал прикладных и фундаментальных исследований. – 2022. – № 3. – С. 59-64;URL: https://applied-research.ru/ru/article/view?id=13368 (дата обращения: 23.11.2024).