Интерес к газовым смесям вызван их широким распространением в природе и применением в различных отраслях промышленности. Газовые смеси используются при производстве и регенерации катализаторов, в фармацевтической промышленности, при производстве биодизельного топлива (рапс + спирт), при повышении нефтеотдачи (углекислота + нефть), в качестве теплоносителя для ядерных реакторов (Не+N2), для аккумулирования энергии, полученной от альтернативных источников энергии, и во многих других областях. Среди наиболее востребованных смесей можно назвать смеси углекислого газа с углеводородами, смеси углеводородов, смеси воды с углекислым газом, аммиаком, сероводородом, углеводородами и др.
Важным с научной и практической точки зрения является изучение поведения таких смесей вблизи критической точки и описание состояния смесей с помощью наиболее простого уравнения, члены которого имеют ясный физический смысл, а само оно удобно для моделирования процессов теплопереноса в смеси сверхкритических флюидов (СКФ) [1, 2].
Материалы и методы исследования
В литературе можно найти различные уравнения состояния бинарной смеси, которые учитывают особенности взаимодействия молекул данной пары компонент [3–5]. Как правило, такие уравнения состояния содержат эмпирические константы и предназначены для описания смесей при решении конкретных технических задач. При этом предполагается, что уравнение состояния для смеси имеет тот же вид, что и уравнения для чистых компонент, составляющих смесь. Такая постановка подразумевает необходимость нахождения законов (mixing rules), связывающих коэффициенты в уравнении для смеси с коэффициентами, входящими в уравнения для индивидуальных компонент. Такой подход, в частности, был предложен в работе [6], где проведен анализ зависимостей коэффициентов уравнения состояния Ван-дер-Ваальса для смеси от коэффициентов уравнений для индивидуальных компонент.
Если состояние каждой компоненты описывается уравнением Ван-дер-Ваальса
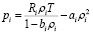, i = 1,2 (1)
и уравнение для смеси имеет тот же вид
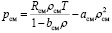, (2)
то согласно этой работе
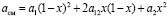, (3)
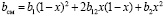. (4)
Здесь считается, что коэффициенты а12 и b12 отвечают за взаимодействие молекул компонент первого типа с молекулами компонента второго типа и являются комбинацией коэффициентов а1 и а2 и b1 и b2.
Однако такой подход имеет ряд недостатков. Во-первых, коэффициент, отвечающий за взаимодействие молекул разных компонент, а12, выражается через коэффициенты а1 и а2, которые в принципе не содержат информацию о взаимодействии молекул разных компонент, поскольку определялись тем или иным способом для однокомпонентного газа. Во-вторых, такой подход достаточно разумен только для бинарных смесей, когда возможно проследить за физическим содержанием выражений коэффициентов смеси через исходные коэффициенты для одной и другой компоненты. Для случая трех и более компонент его реализация будет сопряжена с большими трудностями в связи с необходимостью предложить правила смешения, имеющие ясное физическое содержание.
Более того, даже для двухкомпонентного газа полученное таким методом уравнение может давать как завышенное, так и заниженное по сравнению с реальным давление, что требует введения соответствующей поправки.
Альтернативой описанному может явиться подход, основанный на использовании закона Дальтона, в соответствии с которым давление смеси является суммой давлений компонент. Строго говоря, закон Дальтона справедлив для идеального газа, когда молекулы считаются материальными точками и взаимодействуют друг с другом только при столкновениях. В этом случае в результате суммирования для смеси получается уравнение того же вида (уравнение Клапейрона – Менделеева), что и у исходных компонент с газовой постоянной смеси, выраженной через газовые постоянные компонент.
В случае реального газа, когда необходимо учитывать отталкивание и притяжение молекул, давление смеси может оказаться больше или меньше суммы давлений компонент. А выражение для суммы давлений в общем случае не приводится к виду уравнений для отдельных компонент. В этом случае в выражение для давления должна быть внесена поправка, учитывающая взаимодействие молекул разного типа. Величина этой поправки должна зависеть от конкретного вида потенциала взаимодействия молекул разных типов, входящих в смесь.
Результаты исследования и их обсуждение
В настоящей работе приводится сравнение двух упомянутых подходов для описания состояния бинарной смеси вблизи критической точки. На основе сравнения с экспериментальными данными по конкретным смесям определено оптимальное правило смешения для смеси Ван-дер-Ваальса в рамках первого подхода и найден вид поправки к давлению смеси для второго подхода.
1. Смесь Ван-дер-Ваальса
Согласно [6] значение а12 для большинства веществ лежат в диапазоне от нуля до полусуммы значений коэффициентов а1 и а2 для чистых компонент
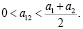
Пусть
,
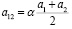где α – некоторый коэффициент 0 ≤ α ≤ 1, представляющий собой долю полусуммы а1 и а2 в значении параметра а12 смеси.
В данной работе сделаны расчеты критической температуры и давления смеси с помощью уравнения Ван-дер-Ваальса (1) для нескольких значений α в сравнении с экспериментальными значениями критической температуры и давления с целью определить оптимальное значение α.
В качестве примера на рис. 1 приведены данные измерений [7] и результаты расчетов критической температуры смеси СO2+SF6. Видно, что наиболее близки к экспериментальным значениям расчетные значения критической температуры при α = 0,75.
На рис. 2 приведены данные измерений и расчетные значения критического давления смеси СO2+SF6 в зависимости от массовой концентрации SF6 для тех же значений α. Видно, что, так же как и для случая критической температуры, наиболее близки к измеренным значения критического давления, полученные для α = 0,75.
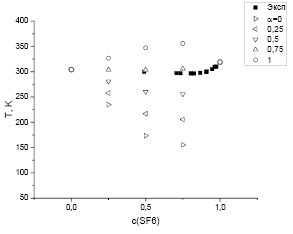
Рис. 1. Расчетная и экспериментальная критические температуры смеси углекислого газа и шестифтористой серы (СO2+SF6) при различных значениях массовой концентрации SF6. ■ – данные измерений [7]
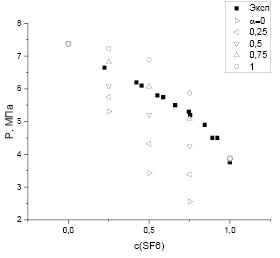
Рис. 2. Критическое давление смеси углекислого газа и шестифтористой серы (CO2+SF6) при различных концентрациях SF6. ■ – данные измерений [7]
2. Уравнение состояния смеси на основе закона Дальтона
Получим уравнение смеси на основе закона Дальтона. Пусть состояние каждой компоненты описывается уравнением Ван-дер-Ваальса (1).
В соответствии с законом Дальтона давление смеси равно сумме давлений компонентов
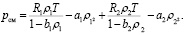(5)
Используя соотношения
,
,
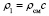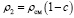где с – массовая концентрация первого компонента, уравнение (5) может быть приведено к виду
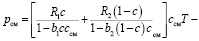
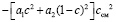. (6)
По этой формуле были проведены расчеты для определения критического давления смеси. При этом критическая плотность смеси вычислялась на основе зависимости, предложенной в [6]. Критическая температура смеси бралась из опытных данных.
Расчет по уравнению (6), которое не учитывает взаимодействия молекул разных компонент, даёт завышенные значения критического давления по сравнению с экспериментом. Ранее ([3]) для коррекции давления, полученного с помощью модифицированного уравнения состояния Бенедикта – Вебба – Рабина, была предложена поправка, учитывающая взаимодействие молекул компонент, пропорциональная произведению молярной концентрации x(1-x) и коэффициентом пропорциональности, зависящим от квадрата плотности. Это дало возможность привести расчетные данные в соответствие с экспериментом. С учетом этого в данной работе вводится аналогичная поправка в виде
А12 с(1 – с) ρ2см,
где А12 – коэффициент, отвечающий за взаимодействие компонент разного вида. При этом уравнение для смеси будет иметь вид
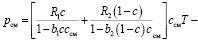
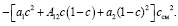(7)
На рис. 3 приведены зависимости критического давления от концентрации для смеси углекислого газа и шестифтористой серы, полученные в эксперименте [7] и раcсчитанные по уравнению без поправки (6) и с поправкой (7) при различных значениях коэффициента А12.
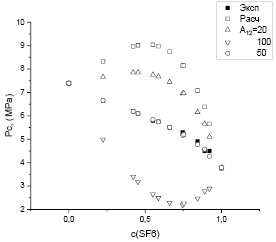
Рис. 3. Критическое давление смеси углекислого газа и шестифтористой серы (СO2+SF6) в зависимости от массовой концентрации SF6 в смеси: ■ – эксперимент [7]
Оптимальные значения параметров a12, A12 и α для различных смесей
|
Смесь |
Ван-дер-Ваальс |
Дальтон |
||
|
a12, м5/кг·с |
α |
A12, м5/кг·с |
α |
|
|
CO2+SF6 |
62,07 |
0,75 |
50 |
0,60 |
|
CO2+CH4 |
363,49 |
0,88 |
160 |
0,39 |
|
CO2+C2H6 |
221 |
0,75 |
200 |
0,68 |
|
C2H6+C3H6 |
464,34 |
1,15 |
343 |
0,85 |
|
C2H4+C3H6 |
481,30 |
1,25 |
350 |
0,90 |
Из рисунка видно, что значения критического давления, полученные по уравнению (6), лежат значительно выше экспериментальных значений. При введении поправки можно добиться хорошего совпадения расчетных и опытных данных. В данном случае наилучшее совпадение имеет место при А12 = 50 м5/с·кг.
Так же как и для случая газа Ван-дер-Ваальса, параметр А12 можно связать с параметрами a1 и a2 для чистых компонент
.
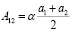Лучше всего расчетные и экспериментальные данные совпадают при α = 0,6.
В таблице представлены оптимальные значения параметров a12, A12 и коэффициента α для различных смесей для расчетов по уравнению Ван-дер-Ваальса смеси и при использовании гипотезы Дальтона с внесением соответствующей поправки.
Заключение
Проведен анализ двух подходов к описанию состояния бинарной смеси, компоненты которой подчиняются уравнению состояния Ван-дер-Ваальса. Первый подход основан на предположении, что смесь также подчиняется уравнению состояния Ван-дер-Ваальса, а коэффициенты уравнения для смеси выражаются через коэффициенты уравнений для чистых компонент. Второй подход основан на предположении, что давление смеси является суммой давлений компонент (закон Дальтона).
В рамках первого подхода проведены расчеты критической температуры и давления для конкретных смесей с помощью уравнения Ван-дер-Ваальса для нескольких значений константы a12. Проведено сравнение с экспериментальными значениями критической температуры и давления и определено оптимальное значение константы a12 для ряда конкретных смесей.
В рамках второго подхода проведены расчеты критического давления с помощью уравнения состояния, полученного суммированием уравнений состояния компонент с соответствующей поправкой к давлению, содержащей константу А12, отвечающую за взаимодействие молекул разных компонент.
Из сравнения с опытными данными определены оптимальные значения константы А12 для ряда смесей. Анализ полученных результатов показывает, что оба подхода удовлетворительно описывают состояние смеси вблизи критической точки и могут быть использованы при моделировании динамики и теплопереноса бинарных смесей.
Работа выполнена в рамках задания по госбюджетной теме № АААА-А20- 120011690131-7.
Библиографическая ссылка
Горбунов А.А., Емельянов В.М., Леднев А.К. УРАВНЕНИЕ СОСТОЯНИЯ БИНАРНОЙ СМЕСИ ВБЛИЗИ КРИТИЧЕСКОЙ ТОЧКИ // Международный журнал прикладных и фундаментальных исследований. – 2022. – № 9. – С. 91-95;URL: https://applied-research.ru/ru/article/view?id=13446 (дата обращения: 25.04.2024).