Сила Лоренца описывается и упоминается в любом учебнике физики. Классическая формулировка: сила Лоренца – сила, действующая на одну движущую заряженную частицу. Модуль силы Лоренца равен произведению заряда частицы, ее скорости, индукции магнитного поля и синуса угла между ними [1].
F = q v B sinα , [1]
где q – абсолютное значение движущегося заряда,
v – скорость движения заряда,
B – модуль вектора магнитной индукции
Исходя из формулы, можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности движения частиц и линий магнитного поля α = 90° и может исчезать при их параллельности α = 0°. Сила Лоренца на частицу, движущуюся со скоростью параллельно вектору B, не действует [2].
Хендрик Лоренц в 1895 г., основываясь на опытах, вывел формулу, которая используется и поныне и носит его имя, как и та сила, что действует на летящую частицу в магнитном поле.
Направление силы Лоренца определяется по правилу левой руки: «Персты левой руки направляются по скорости, магнитные линии должны входить в ладонь, а отогнутый на 90° большой палец покажет направление силы Лоренца в случае движения положительно заряженной частицы» [3]. Формулировка звучит как некое магическое заклинание.
Какова природа боковой силы на движущуюся прямолинейно частицу, если линии магнитного поля расположены вертикально, а смещение происходит горизонтально? В опытах с катодными лучами электроны движутся в вакууме, и поэтому отклонение их магнитным полем является прямым и легко наблюдаемым результатом действия сил Лоренца [4]. Установлено, что чем быстрее скорость частицы в магнитном поле, тем сильнее проявляется центростремительная сила. Основываясь на экспериментальных данных, установили величину бокового смещения заряженных частиц, тем не менее механизм, определяющий боковое смещение, остается нераскрытым. Без выяснения и объяснения причин, порождающих силу Лоренца, эту силу можно смело отнести к классу прикладной магии.
Известно, что к заряженным элементарным частицам относятся частицы, имеющие электрический заряд. Под заряженной частицей понимаем электрон [5]. Известно, что электрон имеет величину заряда равную -1,6×10-19 Кл, массу 9,1×10-31 кг и магнитный момент 9,2×10-24 Дж/Т. Позитрон при массе, равной электрону, имеет противоположную положительную величину заряда, одинаковую массу и магнитный момент. Определенно, электрон и позитрон отличаются только зарядом. При одинаковых физических параметрах электрона и позитрона сила Лоренца воздействует на них противоположно. Взаимодействием частицы с гравитационным полем можно пренебречь из-за малой массы частицы [6]. Необходимо рассмотреть электрон и позитрон и попытаться выделить свойства, определяющие направление силы Лоренца. Направление отклонения движения заряженной частицы в магнитном поле определяется свойствами частицы: магнитным и механическим моментами.
Цель исследования – рассмотреть кинетические свойства частиц, определяющих различное отклонение электрона и позитрона в магнитном поле.
В исследовании рассматривается равномерное магнитное поле. Равномерное магнитное поле наиболее часто визуализируется с помощью параллельных силовых магнитных линий. Представление магнитного поля в виде силовых линий является упрощенным вариантом винтового движения магнитных частиц [7]. В исследовании рассматривается более сложная форма силовых линий (рис. 1). Принимаем, что силовые линии внешнего магнитного поля имеют сотовую структуру, спиралевидную форму и занимают объем равномерно.

Рис. 1. Пространство магнитного поля
Подобное представление магнитного поля позволяет шире рассматривать магнитные взаимодействия на основе кинетических свойств магнитных частиц. Соответственно, для любой заряженной частицы внешнее магнитное поле представляет собой упорядоченную среду из движущихся в потоках магнитных частиц, обладающих определенной кинетической энергией. С увеличением индукции внешнего магнитного поля возрастает кинетическая энергия магнитных потоков.
С другой стороны, магнитное поле электрона, как шароподобного объекта, имеет сферическую форму силовых линий (рис. 2). Отклонение траектории электрона в магнитном поле позволяет сделать вывод о существовании собственного магнитного поля электрона.
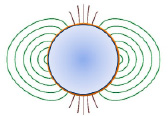
Рис. 2. Классическая форма двухполюсного магнитного поля
Выходящие силовые линии из полюсов охватывают все близлежащее пространство вокруг электрона либо позитрона. Отмечаем, что наиболее важными силовыми линиями являются центральные магнитные линии. Центральные линии не замкнуты и имеют максимальную плотность на полюсах. Данный вывод основывается на рассмотрении гигантских магнитных объектов – магнитных квазаров, имеющих ярко выраженные джеты – центральные магнитные линии, расходящиеся от магнитных полюсов. Боковые линии сферических полей по отношению к центральным линиям являются замкнутыми, более слабыми и, соответственно, второстепенными, поэтому ими можно пренебречь в исследовании.
Для графического изображения магнитного поля целесообразно использовать упрощенную модель, без изображения боковых линий. На рис. 3 изображена упрощенная модель с единственной исходящей спиралевидной магнитной линией из магнитных полюсов, отражающая основной принцип движения магнитных частиц.
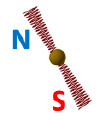
Рис. 3. Упрощенная модель магнитного поля электрона
Вначале рассмотрим магнитное взаимодействие частицы с внешним магнитным полем. Заряженные частицы, влетающие в магнитное поле, могут изначально иметь любую ориентацию собственного магнитного момента ввиду отсутствия каких-либо внешних магнитных сил. При движении в магнитном поле направление магнитного поля частицы становится ориентированным вдоль силовых линий или, точнее, кинетических потоков магнитных частиц. Исходящие винтовые линии магнитного поля электрона интегрируются с внешними потоками магнитных частиц (рис. 4).
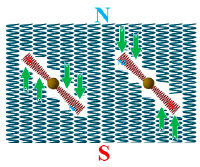
Рис. 4. Моменты сил в зависимости от направления магнитных полюсов
Более мощное внешнее магнитное поле всегда подчиняет более слабое поле элементарных частиц. Любые магнитные частицы переориентируются в постоянное магнитное поле. Под влиянием внешнего воздействия магнитный момент частицы становится упорядоченным и принимает единственно возможное направление (рис. 5).
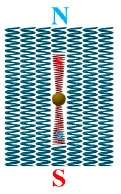
Рис. 5. Уравновешенное положение объекта во внешнем поле
При совпадении направления вращения исходящего потока и потока внешнего поля происходит слияние вращающихся потоков, таким образом, поле заряженной частицы становится частью большего поля. В таком положении кинетическая энергия потока не уменьшается. Направление уже упорядоченного магнитного момента частицы не изменяется при прямолинейном или криволинейном движении. Остальные варианты направления магнитного поля электрона являются невозможными, электрон, подобно магнитной стрелке компаса, всегда разворачивается вдоль силовых линий более мощного внешнего магнитного поля.
Промежуточный вывод исследования заключается в том, что заряженная частица во внешнем поле становится упорядоченной и имеет единственно возможную направленность магнитного поля. Сила, разворачивающая магнитную стрелку и заряженную частицу, является кинетической. Определенно, магнитное поле электрона и позитрона будет одинаково ориентировано.
Рассмотрим проявление силы Лоренца на упорядоченную движущуюся частицу и два возможных направления отклонения (рис. 6).
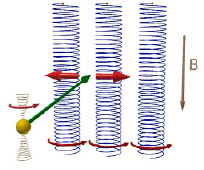
Рис. 6. Два возможных направления силы Лоренца на заряженную частицу
Установлено, что магнитный момент электрона и позитрона ориентирован в постоянном магнитном поле одинаково. Известно, что сила Лоренца будет для них разнонаправлена. По правилу левой руки – электрон всегда отклоняется вправо, позитрон отклоняется влево.
Как известно, у рассматриваемых элементарных частиц имеется собственный механический момент. Собственный момент импульса электрона называется спином. Направление магнитного момента и спина электрона совпадают [8]. Античастица – позитрон будет иметь разнонаправленное направление механического и магнитного момента.
Разница между электроном и позитроном, кроме заряда, заключается только в противоположном направлении механического момента. Ось вращения частицы всегда совпадает с направлением вектора В. Соответственно, плоскость вращения частицы всегда будет перпендикулярна направлению внешних магнитных потоков.
Представим частицу в виде колеса, тогда поверхность крутящегося колеса будет испытывать соприкосновение с перпендикулярными магнитными потоками и отклоняться в сторону. При вращении по часовой стрелке смещение происходит влево, при вращении против часовой стрелки смещение происходит вправо.
Простые кинетические свойства собственного механического момента определяют кинетическое взаимодействие с магнитными потоками магнитных частиц. Кинетическая энергия частицы складывается из двух частей: поступательного движения и вращения вокруг своей оси. Кинетическая энергия отдельных магнитных потоков магнитного поля значительно уступает кинетической энергии частицы. Поэтому влетающая частица не отскакивает упруго от магнитных потоков, а постепенно уменьшается, что вызывает постепенное изменение траектории движения частицы и ее боковое отклонение.
Камера Вильсона наглядно демонстрирует закручивающиеся треки частиц. Форма треков позволяет судить о плавном уменьшении кинетической энергии до нуля. Энергия поступательного движения частицы постепенно расходуется на преодоление магнитной среды. Кинетические свойства магнитной среды выражены через величину индукции магнитного поля. Чем выше индукция магнитного поля, тем выше кинетическое взаимодействие. Определенно кинетическое взаимодействие зависит от угла соприкосновения. Если угол движения частицы с внешними потоками будет близким к 0, то взаимодействие будет минимальным, кинетические соударения будут минимальны.
В то же время при движении кинетическая энергия вращения частицы вокруг собственной оси не изменяется, что подтверждается кольцевым движением частицы в магнитной ловушке.
Заключение
В исследовании рассматривается форма магнитного поля в виде винтовых магнитных потоков. Равномерное постоянное магнитное поле состоит из параллельных вертикальных потоков. Рассмотрена сферическая форма магнитного поля заряженной частицы. Сделано допущение, что боковые линии второстепенны. Основными силовыми линиями частицы являются центральные магнитные линии. Свободная магнитная частица может иметь любое направление магнитного момента. Рассмотрены свойства заряженных частиц: электрона и позитрона. Во внешнем магнитном поле направление магнитного момента и электрона и позитрона противоположно вектору внешнего поля. Сделан вывод, что энергия поступательного движения частицы уменьшается за счет преодоления магнитных потоков и определяется кинетическим взаимодействием. Рассмотрен механический и магнитный момент электрона и позитрона. Если у электрона направление магнитного и механического момента совпадают, то у позитрона направление моментов противоположно. Сила Лоренца определяется направлением вращения механического момента частицы, строго ориентированной во внешнем магнитном поле. За счет ориентированного механического момента электрон отклоняется вправо, соответственно, позитрон, с противоположно направленным механическим моментом, всегда отклоняется влево. В результате исследования делается логический вывод, что сила Лоренца определяется только кинетическим взаимодействием.
Гипотеза имеет научную новизну и имеет теоретическое обоснование. Гипотеза истинна.
Библиографическая ссылка
Карякин А.В., Карякина И.В. ПРИРОДА СИЛЫ ЛОРЕНЦА // Международный журнал прикладных и фундаментальных исследований. 2023. № 4. С. 68-72;URL: https://applied-research.ru/ru/article/view?id=13533 (дата обращения: 24.02.2026).
DOI: https://doi.org/10.17513/mjpfi.13533

