Введение
За последние несколько лет появилась и получила широкое распространение революционная парадигма вычислений, основу которой, в отличие от классических подходов, таких как модель фон Неймана, составляет квантовая механика, а не классическая физика [1]. Как известно, квантовые компьютеры дают возможность находить решения ряда задач, которые были до этого неразрешимы, например факторизация больших чисел, что является центральной проблемой безопасного шифрования данных. В то же время, несмотря на то, что развитие технологий, позволяющих создавать квантовые устройства, все еще находится в самом начале, сегодня уже можно констатировать определенный прогресс в проектировании и управлении квантовыми системами. К примеру, в начале 2024 г. компания IBM объявила [2] о том, что ей удалось создать рабочую квантовую схему, которая смогла успешно разложить 15 на 3 и 5 благодаря применению технологии ядерно-магнитного резонанса.
В контексте вышеизложенного следует отметить, что моделирование квантовых компьютеров представляет собой очень важную задачу в квантовой информатике. Следует принять во внимание тот факт, что полномасштабный квантовый компьютер пока еще не воплощен в промышленных масштабах, поэтому моделирование квантовых компьютеров в настоящее время происходит на классических вычислительных машинах. В настоящее время моделирование квантовых систем – это едва ли не единственный метод, который позволяет протестировать имеющиеся квантовые алгоритмы и фиксировать квантовые эффекты, связанные с передачей и обработкой квантовой информации. Однако, хотя такой способ доступен, у него есть один существенный недостаток: для проведения моделирования на классическом оборудовании необходимы огромные вычислительные ресурсы, что в результате делает широкий спектр задач моделирования просто невыполнимым.
Ряд наметившихся последних тенденций, связанных с автоматизацией электронного проектирования, позволяет значительным образом расширить диапазон автоматизированного моделирования, а именно до:
(i) символического моделирования высокоуровневых программ на Verilog или даже C++;
(ii) решателей полевых уравнений.
В данном контексте, по мнению автора, особого внимания заслуживает альтернатива квантовых симуляторов с открытым исходным кодом, которая может быть реализована с использованием инструментов GNU Octave и Python. Таким образом, исследования в данном направлении представляются актуальными, теоретически и практически значимыми, что и предопределило выбор темы данной статьи.
В то же время, несмотря на то, что сегодня существует ряд обзоров, в которых рассматриваются теоретические и/или экспериментальные аспекты квантовых вычислений, вопрос обсуждения методов моделирования идеальных и физических моделей квантовых компьютеров остается открытым. Также отдельного внимания заслуживают задачи сравнения различных симуляторов с точки зрения их производительности. В дальнейшем развитии нуждаются методы улучшения асимптотического времени и сложности памяти квантового моделирования в случаях, когда задействованные квантовые операторы демонстрируют значительную структуру.
Таким образом, цель исследования заключается в рассмотрении особенностей моделирования квантовых систем с помощью GNU Octave и Python.
Материалы и методы исследования
Основными методами исследования в этой работе являются: методы интеллектуального анализа; методы объектно-ориентированного и функционального анализа; методы численного моделирования; сравнительный анализ.
Результаты исследования и их обсуждение
GNU Octave представляет собой систему компьютерной алгебры (CAS), которая используется для проведения численных, а не символьных вычислений. Главная структура данных в Octave – это матрица, но система также позволяет оперировать C-подобными структурами. Синтаксис языка Octave имеет много схожих черт с языком MatLab. GNU Octave позволяет наблюдать унитарную эволюцию квантовых систем [3]. Этот пакет для моделирования был выбран как инструмент реализации простых вычислений на чистых и смешанных квантовых состояниях, а GNU Octave определена в качестве целевой CAS из-за ее гибкости и переносимости.
С помощью GNU Octave можно моделировать до 10 кубитов. Достоинством GNU Octave является то, что данная система позволяет включить формализм смешанных состояний (матриц плотности), что дает возможность пользователю оперировать на разных уровнях абстракции. Функции нижнего уровня обеспечивают процессы сбора сложных квантовых ворот, в том числе ворот с произвольными управляемыми и целевыми кубитами, также они позволяют готовить чистые состояния и произвольные смеси чистых состояний.
Примерами команд нижнего уровня являются:
− Ket – производит чистое квантовое состояние,
− State – выдает матрицу плотности для данного чистого состояния,
− MixStates – готовит смесь матриц плотности,
− ProductGate – дает возможность построить множество квантовых ворот,
− ControlledGate – позволяет построить управляемые ворота с множеством управляющих и целевых кубитов,
− CNot = ControlledGate.
Последнее равенство указывает на то, что CNot – это сокращение от ControlledGate. Функция принимает в качестве аргументов ControlledGate. Первый аргумент определяет размер выходного гейта, а второй – элементарный гейт, которым нужно управлять. В качестве второго аргумента функции ControlledGate можно использовать любые однокубитовые ворота. Третий и четвертый аргументы этой функции представляют управляемый и целевой кубиты соответственно, при этом функция не будет работать правильно, если они перекрываются [4].
Для моделирования квантовых вычислений в GNU Octave можно использовать различные специализированные пакеты и библиотеки. Ниже приведен список библиотек для GNU Octave, применяемых для моделирования квантовых вычислений, с краткими описаниями.
1. Quantum Package for Octave (QPO). Это специализированный пакет для моделирования и симуляции квантовых систем в Octave. Он содержит множество функций для создания квантовых состояний, операторов, проведения измерений и анализа результатов.
2. QuTiP (Quantum Toolbox in Python). Хотя QuTiP изначально разрабатывался для Python, он также может использоваться в Octave благодаря совместимости синтаксиса и возможности вызова Python-скриптов из Octave.
3. MATLAB Quantum Computing Toolbox. Несмотря на то, что этот инструмент предназначен для MATLAB, многие его функции могут быть перенесены в Octave с минимальными изменениями.
Рассмотрим конкретные примеры практической реализации моделирования квантовых систем с помощью GNU Octave.
Схема подготовки состояния Белла
Схема подготовки состояния Белла (EPR) применяется для целей генерации двух максимально запутанных квантовых состояний (EPR-пары). Цель использования данной схемы заключается в проверке неравенств Белла в квантовой механике [5, 6]. Она состоит из ворот CNOT и ворот Хадамарда. Математическое представление этих ворот имеет следующий вид:
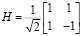

На рис. 1 показана схема подготовки состояния Белла.

Рис. 1. Алгоритм генерации EPR

Рис. 2. Алгоритм подготовки спутанности 3 кубитов
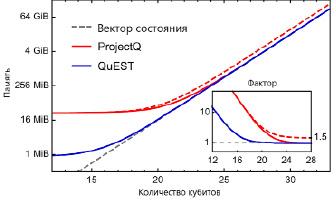
Рис. 3. Потребление памяти процессами QuEST и ProjectQ на Python, о котором сообщает Linux’s/proc/self/status во время моделирования случайных цепей на одном вычислительном узле ARCUS с памятью 256 ГБ
Схема подготовки состояний GHZ
Схема GHZ (названная в честь ее создателей Гринбергера, Хорна и Цайлингера) используется для генерации трех или более максимально запутанных квантовых состояний. В ней также применяются ворота Хадамарда и CNOT [7–9]. На рис. 2 показана схема, которая используется для генерации трех максимально запутанных кубитов и подготовки трехквантового состояния GHZ.
Также отдельного внимания заслуживают симуляторы квантовых вычислений, которые могут найти свое эффективное применение для оптимизации производительности. Например, QuEST и ProjectQ – они представляют собой квантовую вычислительную среду с открытым исходным кодом, включающие компилятор, ориентированный на квантовое оборудование, и квантовый компьютерный симулятор C++ с интерфейсом Python. Оба симулятора хранят чистое состояние в 2n комплексных числах с плавающей запятой для системы из n кубитов, с двойной точностью в каждой мнимой и вещественной компоненте. В случае необходимости QuEST может быть настроен на применение четверной или одинарной точности. QuEST и ProjectQ хранят состояние в примитивах C/C++, и поэтому (по умолчанию) потребляют 16 × 2n B32 только в векторе состояния. Однако для ProjectQ могут быть характерны накладные расходы памяти × 1,5 когда осуществляется распределение состояния [10]. Традиционные затраты памяти, характерные для обоих симуляторов в рамках одного потока представлены на рис. 3, как видно, они незначительно отличаются от затрат в многопоточном режиме.
В то время как QuEST позволяет напрямую читать и записывать вектор состояния, в ProjectQ выборка одной амплитуды имеет накладные расходы на Python, а запись поддерживается только в пакетном режиме, что требует больших затрат памяти, поскольку объекты Python занимают больше памяти, чем сопоставимый примитив C – до 3×33,34. Таким образом, итерация вектора состояния в ProjectQ либо очень медленная, либо требует значительных затрат памяти, что может ограничить ее полезность в некоторых приложениях моделирования.
Стоит отметить, что наряду с рассмотренными программными пакетами и языками программирования существует большое множество других инструментов моделирования квантовых вычислительных процессов. Многие современные компании занимаются перспективными разработками в данном направлении.
Заключение
Квантовые вычисления – это новая парадигма вычислений, использующая принципы квантовой механики. Ее теоретическая основа допускает вычислительную мощность, экспоненциально превышающую классические компьютеры. Однако, учитывая зарождающуюся стадию данной парадигмы и технические трудности в поддержании квантовых битов (кубитов), практические квантовые компьютеры все еще находятся в экспериментальной разработке. В данном контексте особое значение приобретает моделирование квантовых систем.
В статье рассмотрены особенности моделировании квантовых схем с использованием GNU Octave и Python. Эти инструменты для квантового точного моделирования позволяют проводить эффективные симуляции квантовых систем, а также реализовывать вычисления со смешанными состояниями.
Библиографическая ссылка
Тырышкин С.Ю. МОДЕЛИРОВАНИЕ КВАНТОВЫХ СИСТЕМ С ПОМОЩЬЮ GNU OCTAVE И PYTHON // Международный журнал прикладных и фундаментальных исследований. 2024. № 11. С. 50-54;URL: https://applied-research.ru/ru/article/view?id=13672 (дата обращения: 30.01.2026).
DOI: https://doi.org/10.17513/mjpfi.13672

