Введение
Согласно современным представлениям [1] под поверхностной фазой понимают сверхтонкую пленку (поверхностный слой – ПС), находящуюся в равновесном состоянии с кристаллической основой (подложкой), свойства и структура которой отличны от объемных свойств. Однако теоретически толщина этого ПС была определена недавно в работе [2]. Уравнение для толщины ПС выглядит эмпирически следующим образом [2]:
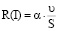[м] (1)
Толщина ПС некоторых АГМ [2]
|
АГМ |
R(I), нм |
АГМ |
R(I), нм |
АГМ |
R(I), нм |
АГМ |
R(I), нм |
|
Be |
0.8 (3) |
Cu |
1.2 (3) |
Mo |
1.8 (5) |
Re |
1.5 (5) |
|
Al |
1.6 (4) |
Ag |
1.7 (4) |
W |
1.6 (5) |
Fe |
1.2 (3) |
|
Si |
2.1 (4) |
Au |
1.7 (4) |
Mn |
1.1 (2) |
Co |
1.1 (3) |
|
Ge |
2.4 (4) |
Cr |
1.2 (4) |
Tc |
1.4 (5) |
Ni |
1.1 (3) |
В уравнение (1) входит только одна величина – молярный объем элемента, который равен υ = M / ρ (М – молярная масса, ρ – ее плотность), S = 1м2. α = 1,17 ∙ 10–9 – постоянная.
Для некоторых атомно-гладких металлов (АГМ) толщина ПС показана в таблице.
Цель исследования. В работе предлагается модель квантовой структуры поверхностного слоя атомно-гладких металлов и ее свойства.
Результаты исследования и их обсуждение
По формуле (1) и литературным данным о молярной массе M и плотности ρ вычислена толщина поверхностного слоя АГМ.
В таблице представлены кристаллы АГМ, отвечающие критерию Джексона [3, с. 40] – α = ΔH / kT, где ΔH – энтальпия, k – постоянная Больцмана, T – температура. Считается, что α > 4 свидетельствует об АГМ, α < 2 – о шероховатых металлах (ШМ), значения же 2 < α < 4 соответствуют промежуточному типу поверхности. Из 54 металлов к ШМ относятся 11 металлов; к АГМ – 30 металлов; к промежуточному типу – 13 металлов.
Из таблицы следует, что толщина ПС АГМ составляет 1–2 нм, а число монослоев (в скобках таблицы, n = R(I) / a, a – постоянная кристаллической решетки) составляет 3–5. ПС R(I) представляет собой наноструктуру. Движение электрона металла в одномерной прямоугольной потенциальной яме с бесконечно высокими «стенками» изложено во всех учебниках по квантовой физике. Уровни энергии En в такой яме равны
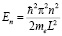. (2)
Здесь me – масса электрона, L – глубина потенциальной ямы.
Учтем L = R(I) и получена формула [2]:
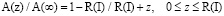– нанослой,
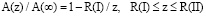– мезослой, (3)
A(z) = const – объемная фаза
где A(z) – физическое свойство нано- и мезослоя; A(∞) – физическое свойство объема.
Если принять A(z) = En(z) – уровню энергии, то при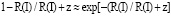 
1 – будет в нанослое 
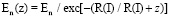. После этого уровень En, то есть при z = 0 и при z = R(I), будет равен: 
; 
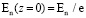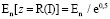. Здесь 
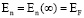– уровень Ферми. Все сказанное выше показано на рис. 1.
На рис. 1 представлена схема металла. Слой толщиной R(I) назван нанослоем, где происходят размерные эффекты коллективного типа. В среднем он содержит 3 монослоя, которые отличны друг от друга. Особенно это проявляется для природного графита, где число монослоев также равно 3. Экспериментально толщину слоя R(I) можно оценить методом рентгеновской дифракции под скользящими углами (РДСУ) [1]. Принципиальная схема метода РДСУ показана на рис. 1, б. Пучок Х-лучей 2 из источника 1 попадает на образец 3 под углом α, равного от долей до одного градуса, Дифрагированный пучок под углом 2θ попадает на детектор 4. Несмотря на простоту схемы метода РДСУ, провести измерение толщины поверхностного слоя чистых металлов R(I) довольно сложно и вот почему. Чтобы измерить R(I), нужно: во-первых, сверхвысокий вакуум – 10–9 – 10–10 Па [4; 5]; во-вторых, нужна атомно-гладкая поверхность [6; 7, с. 10]; в-третьих, довольно мощный источник Х-лучей, в качестве которого в методе РДСУ используют синхротронное излучение [8; 9, с. 13]. Для кристаллов кремния метод РДСУ дает 3,1 нм [1, с. 88] и 2,0 нм [10, с. 181], а для золота – 1,2 нм [1, с. 88] и 1,9 нм [10, с. 181]. Средние величины для кремния R(I) = 2,5 нм и для золота R(I) = 1,5 нм, что почти совпадает с таблицей и подтверждает модель (1).
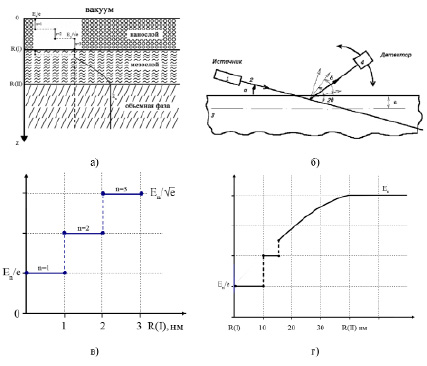
Рис. 1. Схема металла: нанослой → мезослой → объемная фаза (а); схема метода РДСУ (б); схема зависимости уровня энергии En в нанослое (в) и в мезослое (г)
Интерес к таким субмонослойным структурам (в нашем случае к нанослоям R(I)) возрос в последнее время в связи с созданием уникальных, невозможных в объемном состоянии, поверхностных биметаллических соединений. Обсуждается гигантский магниторезистивный эффект (GMR) [11]. Физической причиной гигантского магнитосопротивления металлических наноструктур является спин-зависимое рассеяние электронов проводимости. Эффект GMR реализуется в наноструктурах, у которых соседние ферромагнитные слои связаны обменным взаимодействием. Поэтому толщина слоев должна составлять десятые доли или единицы нанометров. Для получения максимального GMR выбирают толщину спейсера на первом максимуме эффекта около 0,9–1,2 нм. В качестве ферромагнитных используют железо, никель кобальт и их сплавы, металлы V, Cu, Ag, Au, Cr, Mo применяют как материал спейсера. Если сравнить с таблицей, то видно, эти толщины металлических наноструктур содержат 1–3 монослоя.
Из таблицы видно, что для АСМ триады железа (Fe, Co, Ni), включая Cu,n = 3 монослоя, для АСМ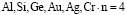 
монослоя, для АСМ 
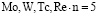монослоев.
Рис. 2, в, показывает, что уровень энергии En(z) изменяется ступенчатым способом, а уровень энергии En(x,y) изменяется непрерывно. Дискретность уровня En(z) вызвана пространственным ограничением волновых функций системы.
В работе [12] приведен обзор результатов исследований квантово-размерных эффектов в тонких пленках металлов (Au, Ag) на поверхности тугоплавких металлов (W(110),Mo(110)) и d-металлов Ni(111), начиная с субмонослойных покрытий и до толщин порядка десяти монослоев, полученных методом фотоэлектронной спектроскопии с угловым разрешением. В этой же работе показано, что поверхностный слой до 6–8 монослоев можно считать квантовой системой при любой температуре. Это подтверждают уравнение (1), таблица и рис. 2, в.
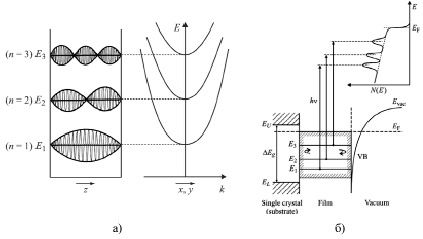
Рис. 2. Квантование вдоль оси z в виде электронных стоящих волн и дисперсионные зависимости в направлении (x,y), имеющие непрерывный характер (а); ограничение волновых функций в пленке d = L = R(I). Данное размерное ограничение приводит к квантованию электронной структуры валентной зоны (энергии E1,E2,E3 ) (б) [12]
Поскольку уравнение (2) описывает качественно квантовые состояния слоя R(I), то используют и другие модели. Суть классической фазовой модели [12] заключается в следующем: условия формирования стоячих электронных волн в пленке (рис. 2, а) определяются на основе учета фазовых изменений при отражении электронной волны от обеих границ пленки и при прохождении электронной волны внутри пленки (рис. 2, б), которые связаны следующим фазовым уравнением:
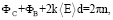(4)
где ФС – изменение фазы при отражении от подложки (кристалла), ФВ – изменение фазы при отражении от поверхностного потенциального барьера, 2kd – набег фазы при прохождении электронной волной толщины пленки (d = L = R(I)). При этом зависимость k(E) определяется дисперсионными электронными соотношениями.
Если пленку металла заменить линейной атомной цепочкой, то уравнение (4) примет вид
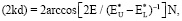(5)
где 
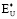и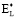 
– верхняя и нижняя границы зоны, формирующей квантовые состояния.
Уравнение (5) представляет расширенную фазовую модель, его можно решить графически [12], но оно отвечает только одной квантовой цепочке. Из таблицы следует, что нужно учитывать 3–5 квантовых цепочек в слое R(I).
Рассмотрим слой R(I) с другой точки зрения. Соответствие поверхностного слоя (ПС) твердого тела его наночастице было предложено академиком А.И. Русановым [13]. Считается, что в наноструктурах роль температуры играет размер. Отсюда следует вывод, что поверхностный слой R(I) представляет собой квантовую структуру при низкой температуре, поскольку T → R(I). В нашем случае поверхностный слой R(I) представляет собой квантовую структуру при любой температуре.
В начале ХХ в. академик А.Ф. Иоффе исследовал кристалл поваренной соли NaCl на прочностные свойства. В своем эксперименте он получил разрыв NaCl на уровне 0,4 кг/мм2, а Макс Борн по квантовой теории получил разрыв NaCl на уровне 200 кг/мм2. А.Ф. Иоффе связал такое различие с существованием в ПС микротрещин. После этого он опускал кристалл NaCl в воду и измерял микротвердость поверхности кристалла. Микротвердость поверхности увеличивалась при растворении ПС, стремясь к теоретическому значению 200 кг/мм2. Этот эксперимент был назван «эффектом Иоффе». Эффекту посвящено множество работ (например, [14]). Для кристалла NaCl по (1) имеем R(I) = 4,35 нм, и он содержит 8 монослоев. Нужно смыть 8 монослоев NaCl, чтобы получить эффект Иоффе [15].
Академик П.А. Ребиндер в 1956 г. совершил открытие, посвященное понижению прочности металлов под действием расплавов металла, а в дальнейшем адгезионному понижению прочности твердых тел за счет окружающей среды. Все это открыло новое направление в науке – физико-химическая механика. Обзор по эффекту Ребиндера по металлам и горным породам представлен в работе [16]. По современным представлениям основой эффекта Ребиндера является разрыв межатомных связей твердых тел при участии активных компонент внешней среды или под действием механической нагрузки. Макроскопическим индикатором этого процесса является снижение поверхностной энергии. Если обратиться к уравнению (3), то следует, что в ПС при z = R(I) поверхностная энергия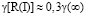 
, то есть в три раза меньше объемной фазы [17], что подтверждает эффект Ребиндера наряду с прочими моментами [18].
Закон Видемана – Франца (ВФ) был установлен эмпирически в 1853 г. и связывает три параметра металла – коэффициенты электропроводности σ и температуропроводности λ с температурой Tи выглядит следующим образом:
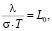(6)
где L0 = 2,21 ∙ 10–8 Вт Ом/К2 – число Лоренца.
Нарушение закона ВФ рассматривалось в многочисленных работах, и это продолжается до сих пор. Отметим только некоторые из них. В работе [19] нарушение закона ВФ связывают с топологической природой волновой функции, отвечающей за транспорт электронов в металле. В качестве примера рассмотрен антиферромагнетик Mn3Ge. Показано, что в широком диапазоне температур (0,5 К < Т < 100 К) число Лоренца L0 = const, а нарушение закона ВФ начинается при Т > 100 K. Считается, что при высоких температурах наблюдается конкуренция между температурой и распределением кривизны Берри. Кривизна электронов по Берри приводит к аномальному эффекту Холла, аномальному эффекту Нернста и аномальному эффекту Риги – Ледука. В работе [20] нарушение закона ВФ связывают с процессом зеркально-диффузного отражения электронов от поверхностей слоя. В основе лежит кинетическое уравнение Больцмана, что является обычным приемов.
Если за физическое свойство A(z) из уравнения (3) принять параметр металла: σ, λ, T входящие в (6), то для числа Лоренца получим картину, аналогичную рис. 1, в, г, что и приводит к нарушению закона ВФ [21].
Аномальный скин-эффект траекторного типа связан с движением отдельных групп эффективных электронов. Эффективными являются такие электроны, которые в скин-слое движутся параллельно поверхности (слою R(I)). Эти электроны создают узкие всплески (листки) тока и поля, медленно затухающие вглубь металла. В недавней работе [22] сформулированы интегральные уравнения Фредгольма второго рода, описывающие поля волн ТЕ- и ТМ-поляризации в металлических пленках с учетом аномального скин-эффекта. Было подчеркнуто, что более корректное описание взаимодействия света с металлом, учитывающее пространственную нелокальность связи векторов j и E, возможно в рамках теории аномального скин-эффекта, основанной на совместном рассмотрении уравнений Максвелла и кинетического уравнения Больцмана и сводящей дело к решению интегро-дифференциальных уравнений для напряженности электрического поля в области металла.
Если за физическое свойство A(z) из уравнения (3) принять удельное сопротивление Ω0 массивного металла, то получим картину, аналогичную рис. 1, в, г. [23].
Постоянная кристаллической решетки a изменяется в слое R(I) из-за реконструкции или релаксации поверхности металла. Это значит, что монослои металла можно представлять как квантовые нити (или квантовые плоскости) с энергией En. Квантовые нити в нанослое R(I) можно трактовать как солитоны. В работе [18] показано, что нанослой R(I) металла подвержен значительным внутренним напряжениям, которые вызывают большое число дефектов и нанотрещин. Эти дефекты могут в металле превращаться (помимо солитона) в краудион, даже при комнатной температуре. Краудионы, которые относятся к топологическим солитонам, в металлах являются очень подвижными, иногда сверхзвуковыми (обеспечивая массоперенос) по сравнению с другими точечными дефектами. Дискретную нелинейную цепочку на рис. 1, в, можно сопоставить дискретным бризерам, которые представляют из себя локализованные моды колебаний.
Заключение
Количественная квантовая модель поверхностного слоя атомно-гладких металлов, описанная уравнениями (1)–(3), может применяться к любым твердым телам. Если элемент поверхностного слоя твердого тела представить как нелинейный конденсатор – вариконд, из-за наличия размерных эффектов, то стали, сплавы черных и цветных металлов, композиционные и керамические материалы можно представлять не как твердые растворы, а как совокупность варикондов, описанных уравнениями (1)–(3). Применяя методы компьютерного моделирования или искусственного интеллекта, можно прогнозировать различные материалы за счет внешнего воздействия: прокатка, термический и лазерный отжиг, ионная имплантация, нанесение покрытий и прочее, для их использования в нано- и микроэлектронике, в авиа- и самолетостроении, машиностроении и т.д.
Библиографическая ссылка
Юров В.М., Гончаренко В.И., Олешко В.С., Жангозин К.Н. КВАНТОВЫЕ СВОЙСТВА ПОВЕРХНОСТНОГО СЛОЯ АТОМНО-ГЛАДКИХ МЕТАЛЛОВ // Международный журнал прикладных и фундаментальных исследований. – 2024. – № 12. – С. 52-57;URL: https://applied-research.ru/ru/article/view?id=13682 (дата обращения: 22.01.2025).