Введение
Особенностью логико-вероятностных моделей надежности сложных систем при использовании метода дерева отказов является принимаемое допущение о возможности описать состояния, принимаемые системой при эксплуатации, в виде значений функции алгебры логики (ФАЛ), аргументами которой являются независимые логические переменные, отображающие состояния ее компонентов. Такая ФАЛ в классической монографии [1] получила называние функции работоспособности системы.
Если переход между состояниями системы меняет условия функционирования элементов, формируя зависимости, используются динамические модели надежности (например, в виде марковских графов), в которых наряду с отказами компонентов учитываются другие факторы. Особенности функционирования системы в этом случае отображены в переходах между состояниями, которые являются основой моделей. Ввиду, как правило, большой размерности моделей, представленных марковскими графами, прямые методы анализа, использующие операции над матрицами интенсивностей переходов, требуют большого объема вычислений.
Цель исследования состоит в развитии подхода, использующего асимптотические соотношения для оценок показателей надежности, получаемые на основе анализа топологии вложенных марковских цепей, что по сравнению с прямыми операциями над матрицами интенсивностей переходов является более эффективным инструментом, понижающим объемы вычислений.
Материалы и методы исследования
Рассмотрим простой пример. Пусть имеется комплекс из трех однотипных резервированных изделий (компонентов комплекса), который теряет работоспособность при отказе всех компонентов. При этом на объекте имеется также пополняемый в процессе эксплуатации комплект запасных частей (ЗИП) в количестве одной единицы изделия. При наличии изделия в составе ЗИП в текущий момент времени, отказавший компонент может быть быстро восстановлен, при этом интенсивность восстановления равна μ1. Если ЗИП исчерпан, он пополняется с интенсивностью μ2 < μ1. В этом примере имеет место зависимость поведения компонентов системы от наличия ЗИП. Модель надежности такого комплекса изделий можно представить в виде графа марковского процесса с конечным числом состояний (рис. 1). Задача состоит в оценке вероятности безотказной работы (ВБР) системы.
Начальным состоянием графа является левое нижнее состояние, обозначаемое парой чисел {0,0}. В этом и других состояниях первое число соответствует текущему количеству отказавших компонентов. Второе число в паре обозначает количество элементов ЗИП, использованных в составе системы, по условию задачи оно не превышает 1. Неработоспособное состояние системы обозначено буквой F. Интенсивности переходов между состояниями вследствие отказов компонентов обозначены соответственно λ, 2λ, 3λ. В такой модели системы число состояний равно семи, однако, если необходимо рассмотреть ЗИП в количестве k единиц, в модели потребуется число состояний, равное 3*(k+1) + 1. Таким образом, применение методов решения подобных задач на практике часто приводит к необходимости построения и анализов графов и матриц интенсивностей переходов большой размерности, что затрудняет вычисления и вызывает дополнительные вопросы оценки точности результатов расчета, усложняет их интерпретацию и анализ основных вкладчиков.
Другой подход к решению подобных задач предполагает, что отношения λ/μ1 и λ/μ2, малы, что выполняется на практике. При данных допущениях ВБР системы асимптотически удовлетворяет экспоненциальному закону, параметр которого может быть вычислен на основе анализа топологии графа и значений вероятностей переходов, составляющих его пути и петли.
Из теории известен ряд приближенных формул для расчета ВБР системы с восстанавливаемыми элементами, основанных на асимптотической теории, например:
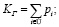
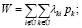
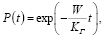(1)
где Ω – множество работоспособных состояний системы Кг – стационарный коэффициент готовности, W – стационарный параметр потока отказов, P(t) – вероятность безотказной работы, pi – стационарные значения вероятностей состояний процесса, описываемого марковским графом. Формула (1) хорошо аппроксимирует значение ВБР системы с восстанавливаемыми элементами при обозначенных выше условиях. Однако можно получить более точную асимптотическую оценку ВБР.
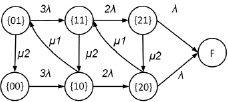
Рис. 1. Граф для задачи оценки ВБР с учетом ЗИП Источник: составлено автором
Обозначим qij – вероятности переходов вложенной цепи между состояниями i и j за один шаг, πiF – результирующие вероятности переходов из состояния i в F, обозначим Si – среднее время перехода из состояния i в любое из состояний, завершающих цикл (F или 0). π0F и S0 представляют, соответственно, вероятность отказа за один цикл, то есть период времени от t = 0 до момента отказа или возврата в начальное состояние, и среднее время цикла.
Оценка ВБР системы при малом π0F вычисляется [2, с. 56] по формуле
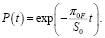(2)
Имеется также нижняя оценка ВБР, справедливая в более широких условиях (не предполагающих малость π0F) [2, с. 58]:
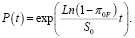(3)
Вычислить входящие в (2), (3) параметры можно, используя метод анализа топологии вложенных цепей. Для введенных выше величин справедливы системы уравнений:
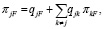(4)
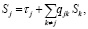(5)
где τj представляет собой среднее время нахождения процесса в состоянии j.
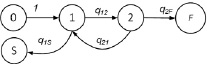
Рис. 2. Пример разомкнутого графа Источник: составлено автором
Чтобы найти общее решение, вначале рассмотрим простую цепь с разомкнутой петлей возврата в начальное состояние (фиксирование начального состояния эквивалентно размыканию его возвратной петли) (рис. 2).
При таком условии другие состояния не влияют на формирование вероятности состояния 0, так как возврат в него невозможен.
Решая системы (4) и (5), в итоге получим (с учетом q01 = 1):
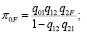
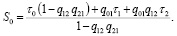(6)
Вычитаемое в знаменателе представляет вероятность единственной петли цепи (между состояниями 1 и 2). Структура левой и правой частей (6) аналогична, если учесть, что для вычисления S0 необходимо πjF заменить на Sj, и добавить вектор свободных членов τj .
Обобщением (6) на произвольный случай являются классические формулы, полученные Мэзоном [3]. Обозначим все прямые пути (то есть пути, не содержащие петель) из вершины 0 в вершину F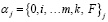 
, j =1,2 … N , а все петли 
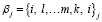, j =1,2 … M.
Определим вероятности путей и петель как произведения соответствующих вероятностей перехода:
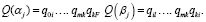
В [3] показано, что в общем случае решение для вероятности перехода из начального состояния (начальной вершины) цепи в состояние отказа дается формулой
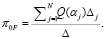(7)
При этом определитель графа Δ представлен знакопеременной формулой (8).
Каждое из слагаемых в (7), начиная со второго, содержит произведения вероятностей пар, троек и других комбинаций непересекающихся петель. Алгебраическое дополнение Δj для j-го пути представляет собой определитель графа, получаемого из исходного удалением вершин, лежащих на этом пути.
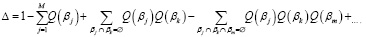(8)
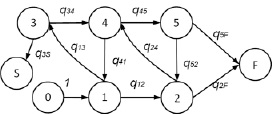
Рис. 3. Граф вложенной цепи переходов для решения задачи Источник: составлено автором
Если вернуться к (6), видно, что в числителе левой формулы записана вероятность прямого пути из 0 в F, а в числителе правой – произведения вероятностей прямых путей из i = 0 в j = 0,1,2 и τj. Кроме того, в первом слагаемом присутствует множитель Δ00 =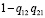 
, представляющий алгебраическое дополнение для начальной вершины (он равен определителю графа). Для путей из начальной в другие вершины Δ0j = 1, так как вершины, входящие в петлю, присутствуют в каждом из путей. Преобразовав исходный граф на рис. 1 во вложенную цепь и перенумеровав для удобства вершины, получим граф на рис. 3.
Граф содержит 3 петли и 4 прямых пути из начальной вершины в F. Поэтому для данного графа по аналогии с предыдущим примером запишем решение:
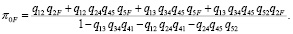(9)
Пути являются взаимоисключающими последовательностями событий. Например, первый и второй пути содержат два несовместных события с переходами из состояния 2, и т.д. Формула, аналогичная (9), может быть легко получена также и для S0.
Выше рассмотрены асимптотические методы анализа на основе вычисления вероятностей переходов, позволяющие заменить матричные вычисления анализом топологии графа вложенной цепи. Данный расчетный метод является более экономным в отношении объема вычислений (на графе имеется 7 путей и петель, в то время как размерность матрицы интенсивностей переходов исходного графа составляет 7*7). В данном примере это несущественно, однако для больших моделей необходим машинный анализ.
Ниже эти идеи развиваются в направлении применения для анализа вложенных марковских цепей традиционных подходов, базирующихся на методах анализа деревьев отказов (ДО). Для иллюстрации описываемого приема преобразуем граф на рис. 3 в форму традиционного дерева отказов, представленного на рис. 4.
На рисунке введены следующие обозначения: TR## с подчиненным оператором «И» обозначает условие перехода между состояниями системы, причем исходное состояние указывается в идентификаторе первым номером, а последующее состояние – вторым номером; базисные события ## обозначают переход, соответствующий дугам графа на рис. 3. Кроме указанных выше операторов TR## и базисных событий на ДО присутствуют также операторы «И» и «ИЛИ» (с идентификатором TR#, обозначающие условие нахождения графа в каком-то одном из его состояний. Заметим, что ДО на рис. 4 имеет ряд существенных отличий от традиционных деревьев, реализующих ФАЛ, а именно:
‒ базисными (элементарными) событиями ДО являются переходы между состояниями графа, а не отказы элементов системы;
‒ ДО может содержать петли в виде циклических ссылок операторов, которые не следует разрывать до выполнения анализа ДО;
‒ минимальные сечения отказов (МСО), определяемые путем анализа марковских графов переходов, являются несовместными, так как они представляют собой разные пути из начального состояния в состояние отказа.
Поиск МСО и петель деревьев, подобных показанному на рис. 4, может выполняться различными методами, например с использованием алгоритма обхода дерева.
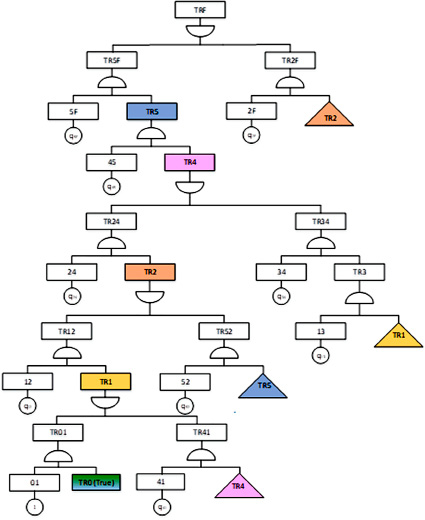
Рис. 4. Дерево отказов для анализируемого графа Источник: составлено автором
Как уже отмечалось, последовательности событий, формирующие прямые пути к вершинному событию, в таких ДО несовместны, однако верно большее – каждый такой путь является минимальным, то есть не содержит в себе другие пути. Сечения, не являющиеся минимальными, при расчете учитываются в (8) за счет вероятностей петель.
Результаты исследования и их обсуждение
Преимущество применения для анализа цепи традиционного ДО (рис. 4) заключается в возможности привлечения стандартного программного обеспечения (ПО), выполняющего поиск МСО и петель. Рассмотрим подробнее способы анализа ДО, представленного на рис. 4.
В этом примере, в результате применения алгоритма обхода ДО слева, при первой итерации формируется путь, состоящий из базовых событий 5F, 45, 24,12, 01. Соответственно, вероятность пути равна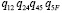 
. Следующая цепь получается заменой операнда в TR1, она заканчивается циклической ссылкой на оператор TR4, то есть формируется петля 24, 12, 41. Вероятность петли 
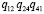. Процесс повторяется, пока не будут выявлены все пути и петли. Окончательный расчет ВБР системы при этом выполняется по формулам (6) и (7). Для графов большой размерности такой подход позволяет не только быстро выполнять расчеты, но также определять доминантные последовательности событий, определяющие результаты вычислений. При этом нет необходимости выполнять отбор МСО среди всех сечений.
Суммируя сказанное выше, можно заключить, что для систем, модели которых представлены в виде больших графов со сложной структурой, для получения оценок показателей надежности можно использовать российское ПО [4–6], реализующее метод дерева отказов. Необходимо отметить также, что марковский граф является прямым аналогом схемы функциональной целостности (СФЦ) [7], что позволяет для решения задач также использовать ПО, разработанное для анализа указанного вида моделей.
Кроме того, эвристически ясная процедура преобразования графа вложенной цепи в ДО, подобного показанному на рис. 4, либо в СФЦ позволяет написать скрипт, автоматизирующий данную конвертацию. Таким образом, трудоемкость процесса анализа фактически сводится к построению самой модели в виде марковского графа.
Заключение
В настоящей статье описан подход к анализу динамических моделей надежности сложных систем на основе марковских графов, позволяющий при приемлемой для практики точности оценок показателей надежности значительно понизить трудоемкость и объем вычислений, поскольку для сложных систем с многочисленными компонентами проблема размерности моделей выходит на первый план. Метод основан на использовании асимптотических соотношений для показателей надежности, определяемых на основании результатов анализа топологии вложенных цепей графов. При этом для выполнения анализа может применяться стандартное ПО, использующее метод дерева отказов или схем СФЦ. Очевидно, что общих правил разработки таких моделей в силу разнообразия решаемых задач не существует. Вместе с тем для ряда задач, подобных описанной выше, построение моделей может быть автоматизировано. В этих конкретных случаях, независимо от сложности решаемой задачи, имеется возможность создания сквозного инструмента анализа.
Библиографическая ссылка
Морозов В.Б., Морозова М.А. МЕТОД РАСЧЕТА НАДЕЖНОСТИ СЛОЖНЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ТОПОЛОГИИ МАРКОВСКИХ ГРАФОВ И ДЕРЕВА ОТКАЗОВ // Международный журнал прикладных и фундаментальных исследований. 2025. № 3. С. 34-39;URL: https://applied-research.ru/ru/article/view?id=13708 (дата обращения: 21.04.2025).
DOI: https://doi.org/10.17513/mjpfi.13708