Введение
В настоящее время водосборная территория речных бассейнов, являющаяся пространственным базисом народонаселения и природопользования и выполняющая важные социальную, экологическую и экономическую функции, в связи с нарушением естественных геологических, биологических и гидрохимических процессов в результате антропогенной деятельности, перешла в активную стадию «сукцессии», которая привела к последовательным и необратимым изменениям в среде обитания человека в пространственных и временных аспектах и которая требует нормирования. В условиях «жесткой» антропогенной деятельности на водосборных территориях речных бассейнов, как объектах комплексного обустройства, обеспечивающих безопасность жизнедеятельности человека, возникает необходимость разработки моделей интегральной оценки здоровья населения, позволяющих дать этому качественному явлению качественную оценку. Актуальность таких научных исследований связана со стохастическим характером возникновения и распространения заболеваний населений, требующих построения интегрального показателя, обеспечивающего единую оценку здоровья населения [1–3], на основе различных статистических методов с использованием медико-демографических показателей, позволяющих оценить темп и направленность изменения не только отдельных видов заболеваемости населения, но и спрогнозировать их временные аспекты, для разработки мероприятий по обеспечению улучшения здоровья населения.
Цель исследования – разработка математической модели интегрального показателя для оценки состояния здоровья населения с целью оперативной оценки ситуации и принятия управленческих решений.
Задача исследования – научное обоснование методологии построения математических моделей с использованием методов математической статистики, теории вероятности и агрегирования частных показателей для решения многопараметрических задач, обусловленных по выбору вида заболеваемости населения, разработка интегрального индекса здоровья населения, позволяющего их спрогнозировать во временных аспектах.
Материалы и методы исследования
Методы исследования поставленных задач основаны на материалистической теория научного познания, основанной на методах математической статистики, теории вероятности и средних значений.
Существует большое количество научных работ для оценки состояния здоровья населения с использованием интегральных индикаторов, базирующихся на построении многопараметрических моделей, среди которых следует выделить работы В.А. Медик и М.С. Толмачева [4], А.Г. Кулак [5], В.В. Мешечкина и Н.И. Богатыревой [6], базирующихся на теории математической статистики и теории вероятности.
В работе Б.Ф. Кирьянова [7], где для расчета интегрального показателя состояния общественного здоровья используются многопараметрические модели интегрального показателя (IP), одновременно учитывающий весовой коэффициент по видам заболеваемости:
 , (1)
, (1)
где WCi – весовые коэффициенты; SIi – i-ый показатель системы или i-ая переменная параметров, характеризующих состояние системы; n количество переменных показателей.
Для сравнительного анализа и оценки здоровья населения удобно использовать нормированный интегральный показатель IPi ∈ [0;1] и все показатели здоровья населения SIi ∈ [0;1] , которые представляются в относительных величинах, то есть в виде безразмерных величин.
Одним из фундаментальных направлений в области оценки здоровья населения является направление, развиваемое в работах А.Г. Кулака, где индекс здоровья населения [8] сформирован на основе методики Index-Numbers [9], базирующейся на «теории средних величин» известного английского статистика А. Боули [10]. Предложенная математическая модель здоровья населения А.Г. Кулака базируется на IndexNumbers и показателях, предлагаемых Всемирной организацией здравоохранения (ВОЗ) с использованием статистической информации организации здравоохранения, где в подготовительном этапе рассчитываются стандартизированные значения этих показателей для приведения исходных данных до сопоставимого вида по следующему выражению [8, с. 71]:
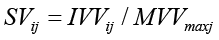 , (2)
, (2)
где SVij – стандартизированное значение j-го показателя в i-м интервале времени ( ,
,  ); IVVij – исходные значения переменных; MVVmaxj – максимальное значение j-го показателя за весь исследуемый период.
); IVVij – исходные значения переменных; MVVmaxj – максимальное значение j-го показателя за весь исследуемый период.
Проведенный анализ существующих подходов к математическому моделированию интегрального показателя здоровья населения показал, что в целом они разработаны на основе данных статистики показателей заболеваемости и инвалидности, физического развития населения, обеспеченности здравоохранения и образованности населения и факторов окружающей среды.
Результаты исследования и их обсуждение
Алгоритм построения интегральных показателей здоровья населения, основанных на статистических показателях здравоохранения, системе линейных алгебраических уравнений, базирующихся на теории регрессивно-корреляционного анализа, который состоит из пяти последовательных этапов, где в зависимости от решаемых задач, применяются различные методы исследования.
Первый этап. Обоснование системы важнейших медико-статистических показателей, влияющих на здоровье человека, установления источников информации для ее сбора, оценивается достоверность и надежность исходных статистических данных, для создания базы исследования.
Второй этап. На основе многолетних важнейших медико-статистических показателей, для выявления тенденции их изменения, с использованием корреляционно-регрессионного анализа, анализа временных рядов, статистических графиков и таблиц, определяются следующие статистические показатели:
– виды линейных уравнений трендов показателя заболеваемости населения:
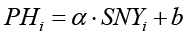 ;
;
 ;
;
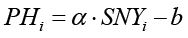 , (3)
, (3)
где PHi – годовые показатели заболеваемости населения на 100 тыс. человек; α – коэффициент регрессии; b – показатель, характеризующий увеличение следующего значения временного ряда; SNYi – номер периода или порядковый номер года;
– среднеарифметическое значение годовых показателей заболеваемости населения (AAPHi), определяется как число, равное всем числам множества, деленное на их количество:
 , (4)
, (4)
где ni – количество лет за периоды;
– модульный коэффициент годовых показателей заболеваемости населения (MCPHi), безразмерная характеристика, отношение какой-либо варьирующейся (изменяющейся) во времени величины к его среднеарифметическому значению:
 . (5)
. (5)
Третий этап. Для количественного представления значимости медико-статистического показателя обычно используются весовые коэффициенты интегрального показателя здоровья населения, базирующиеся на математической теории важности критериев, составляющей одно из направлений теории принятия решения, выбор которых обеспечивается на основе их парного сравнения в условиях полной определенности [11; 12]. Основой для расчета весовых коэффициентов каждого медико-статистического показателя является амплитуда/размах статистических показателей (RSIPHi), характеризующих разность максимальных и минимальных значений признаков в совокупности здоровья населения:
 ,
,
где RSIPHi – амплитуда размах статистических показателей здоровья населения; PHmaxi, PHmini – соотвественно максимальное и минимальное значения i-го показателя, характеризующего здоровье населения.
Для обобщения характеристики различия медико-статистического показателя здоровья населения с помощью абсолютных показателей, выраженных в единицах, не всегда возможно и в этих случаях для сравнительной оценки степени различия используются относительные показатели размаха статистических показателей здоровья населения, выраженные в относительных единицах в виде коэффициента относительного разброса показателей здоровья населения (RSCPHi) по следующей формуле:
 . (6)
. (6)
На основе коэффициента относительного разброса статистических показателей можно определить весовой коэффициент линейных моделей интегрального показателя здоровья населения по следующему выражению:
 , (7)
, (7)
где WCPYIi – весовой коэффициент показателей здоровья населения; ni – число показателей здоровья населения.
Значения весовых коэффициентов показателей здоровья населения определяются таким образом, чтобы их алгебраическая сумма равнялась единице, то есть
 [13; 14].
[13; 14].
Четвертый этап. В качестве метода исследования для математического моделирования интегрального показателя здоровья населения используется метод обобщенных или интегральных оценок показателей, характеризуемых неоднородными количественными и весовыми параметрами, базирующихся на теории событий и анализа ситуации, где согласно В.Е. Минакеру [15], в качестве интегральной оценки принимается арифметическая сумма оценок частных параметров здоровья населения:
 , (8)
, (8)
где IAPHi – интегральная оценка частных параметров здоровья населения; PPPHi – оценка i-го параметра здоровья населения.
Медико-статистические показатели имеют неодинаковую важность для здоровья населения, и для решения этих особенностей частных параметров здоровья населения возникает необходимость во введении коэффициентов весомости параметров, тогда формула для интегральной оценки частных параметров здоровья населения принимает следующий вид:
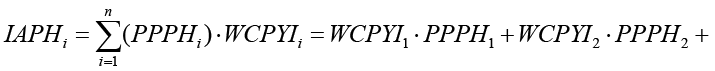
 , (9)
, (9)
где WCPYIi – весовой коэффициент i-го параметра здоровья населения.
Изложенные выше результаты сопоставительного анализа существующих методов построения интегральной оценки частных параметров здоровья населения показали возможность использования для оценки здоровья населения интегрального показателя (IIPHi), который определяется на основе суммирования средневзвешенных арифметических показателей частных параметров здоровья населения:
 , (10)
, (10)
где WCPYIi – весовой коэффициент показателей здоровья населения; ni – количество показателей здоровья населения.
Пятый этап. При количественной и качественной оценке интегрального показателя здоровья населения (IIPHi), в связи с существованием на практике разнонаправленных тенденций изменения во времени, необходимо выявить причинно-следственные связи основных факторов, влияющих на показатели здоровья населения (PHi). Для оценки причинно-следственных связей основных факторов можно использовать их амплитуды колебания (ΔIIPHi) в рассматриваемых промежутках времени (PTi):
 , (11)
, (11)
где IIPHimax – максимальное значение IIPHi в рассматриваемом промежутке времени; IIPHimin – минимальное значение IIPHi в рассматриваемом промежутке времени.
При этом изменение интегрального показателя здоровья населения (IIPHi) в соответствии с разбросом статистических показателей от IIPHimin до IIPHimax, будет изменяться пропорционально вкладам весового коэффициента (WCPYIi) показателей здоровья населения (PHi).
Таким образом, предложенный подход для оценки интегрального показателя здоровья населения, базирующийся на теории регрессивно-корреляционного анализа, амплитуды размаха статистических показателей, метода анализа ситуации, теории событий и интегрального показателя, как обобщающей характеристики здоровья населения, может быть использован для решения проблем здравоохранения при наличии соответствующих статистических материалов.
Заключение
В результате проведенного исследования выполнена систематизация и структурный анализ существующих методов оценки здоровья населения, с позиции использования их для решения комплексной задачи здравоохранения, на основе всех частных параметров здоровья, представленных в соответствующих статистических сборниках.
Временные ряды здоровья населения, полученные на основе государственных статистических данных, как случайные величины, зависящие от времени и начальных условий, требуют определить среднеарифметическое значение годовых показателей заболеваемости населения, виды линейных уравнений трендов показателя заболеваемости населения и модульный коэффициент годовых показателей заболеваемости населения с использованием метода тенденций.
При этом динамике заболеваемости во времени свойственна не только стохастическая составляющая, но также и детерминированная составляющая в виде тренда, с разнонаправленными (положительными и отрицательными) трендами и их функциональные зависимости в виде корреляционно-линейных уравнений с двумя переменными, служащие научной основой для прогнозирования медико-демографического состояния региона.
Использование метода обобщенных или интегральных оценок показателей, характеризуемых неоднородными количественными и весовыми параметрами, основанных на теории событий и анализе ситуаций с использованием математического моделирования интегрального показателя здоровья населения, позволяет учесть все виды заболеваемости, представленные в государственных статистических сборниках, и преобразовать их в единый показатель, удобный для прогнозирования их тенденций в пространственных и временных аспектах.
Рассмотренные в работе подходы по созданию базы исследования и методологические подходы, направленные на разработку алгоритма расчета интегрального показателя с применением теории регрессивно-корреляционного анализа, амплитуды размаха статистических показателей, метода анализа ситуации, теории событий и средних величин, позволяющие оценить и спрогнозировать медико-демографическое состояние во времени, на основе оценки тенденции изменения с использованием линейных трендов.
Конфликт интересов
Библиографическая ссылка
Мустафаев Ж.С., Мустафаева М.Б. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИНТЕГРАЛЬНЫХ ПОКАЗАТЕЛЕЙ ОЦЕНКИ ЗДОРОВЬЯ НАСЕЛЕНИЯ // Международный журнал прикладных и фундаментальных исследований. 2025. № 11. С. 11-15;URL: https://applied-research.ru/ru/article/view?id=13766 (дата обращения: 11.02.2026).
DOI: https://doi.org/10.17513/mjpfi.13766

