Виртуализация процесса защиты непрерывной информации заключается в установлении условий виртуализации, оптимизирующих этот процесс, и определении решений, соответствующих данным условиям. Отличительной особенностью процесса защиты непрерывной информации является высокая избыточность непрерывных сообщений, которую, как правило, не удается в полной мере устранить в формируемых криптограммах.
В процессе синтеза модели оптимальной защиты непрерывной информации с позиций виртуализации относительно условий теоретической недешифруемости устанавливались основные условия теоретической недешифруемости и определялись теоретические основы защиты непрерывной информации (скремблирования) для установленных условий. Основу определения условий обеспечения абсолютной недешифруемости при защите непрерывной информации составляло определение теорем скремблирования.
Теорема 1. Теорема цифрового скремблирования. Пусть скремблирование определяется непрерывным ансамблем сообщений S, дискретным ансамблем криптограмм E и дискретным ансамблем ключей K. Пусть дискретный ансамбль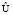 
является ансамблем виртуальных сообщений, полученным в результате виртуализации непрерывного ансамбля S. Тогда, если среднее количество взаимной информации равно
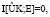(1)
то всегда существует цифровое скремблирование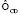 
, обеспечивающее теоретическую недешифруемость.
Теорема 2. Теорема виртуализации цифрового скремблирования. Пусть скремблирование определяется непрерывным ансамблем сообщений S, дискретным ансамблем криптограмм E и дискретным ансамблем ключей K. Пусть дискретный ансамбль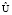 
является ансамблем виртуальных сообщений, полученным в результате виртуализации непрерывного ансамбля S. Пусть элементы выборочного пространства ансамбля 
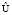формируются в результате цифрового компандирования сообщений выборочного пространства ансамбля S. Тогда, если при цифровом скремблировании, заданном дискретными ансамблями ключей K и криптограмм E, средняя взаимная информация 
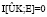, то всегда и только всегда будет справедливо равенство 
.
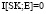Теоремы 1–2 определяют обобщенную модель виртуализации защиты непрерывной информации с позиций условий теоретической недешифруемости. Особенностью полученной модели является предусматриваемая виртуализация алгоритма формирования ключей, осуществляемая путем обеспечения адаптивно регулируемой неопределенности состояний источника ключа. Ансамбль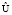 
является результатом виртуализации ансамбля S непрерывного источника информации. Таким образом, эффективность обобщенной модели процесса защиты непрерывной информации, с позиций условий теоретической недешифруемости, зависит от установленных условий виртуализации непрерывного источника информации.
Основу виртуализации непрерывных источников при цифровом скремблировании составляет цифровое компандирование, предусматривающее компрессию при скремблировании и экспандирование при дескремблировании. С этих позиций к основным условиям виртуализации непрерывных источников при цифровом скремблировании относятся: 1) минимизация информационных потерь; 2) обеспечение минимальной избыточности.
Полученная модель составляет фундаментальную основу стратегии оптимизации процесса защиты непрерывной информации, открывающей принципиально новую область возможностей разработки методов скремблирования, обеспечивающих абсолютную недешифруемость.
Библиографическая ссылка
Котенко В.В., Румянцев К.Е., Поляков А.И., Ежов А.И. МОДЕЛЬ ОПТИМАЛЬНОЙ ЗАЩИТЫ НЕПРЕРЫВНОЙ ИНФОРМАЦИИ // Международный журнал прикладных и фундаментальных исследований. – 2013. – № 8-3. – С. 124-125;URL: https://applied-research.ru/ru/article/view?id=3918 (дата обращения: 26.04.2024).