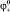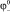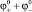Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы
• Литература

Кочешкова Л.Г. 1 Суворов Д.В. 1 Палашов В.В. 1 Кочева М.А. 1

---

1 Нижегородский государственный архитектурно-строительный университет

Статья в формате PDF

407 KB

1. Палашов В.В. Электродинамический расчет катодной защиты / В.В.Палашов, И.В. Палашов, С.Н. Жиляев / Изв. канд. инженер. наук им. А.М. Прохорова. – М.; Н. Новгород, 2005. –Т.15. – С. 106–109.

2. Палашов В.В. Закономерность изменения углов преломления потоков электромагнитной энергии заряженных ионов, движущихся встречно под воздействием ЭДС в грунтовых и водных средах. – М.: Открытие, диплом № 403, рег. № 506, 2010.

3. Кочешкова Л.Г., Кочева Е.А., Палашов В.В. Расчет электрических параметров в грунтовых и водных средах // Успехи современного естествознания. – 2012. – № 6. – С. 170–172.

В статье рассмотрена инновационная модель исследования механизма проводимостей в системе катодной защиты. Для изучения механизма проводимостей в грунтовых электролитах под воздействием постоянной или выпрямленной ЭДС была выбрана электродная система, представляющая собой наибольшие параметры электродов и среды, встречающиеся в технике – катодная защита. Используя аналогию понятий законов Снеллиуса, Максвелла, учитывая локализацию электромагнитной энергии (вектор Пойнтинга) и закон Фарадея (движения материальных частиц ионов и катионов) позволяет подобрать математическую функцию удобную для практического использования данных, полученных прямыми измерениями в проводниках второго рода, а также легко выявить оригинальные связи и явления, происходящие в системе катодной защиты, имеющей огромное значение в сохранение экологической безопасности и экономике.

Постановка задачи. C целью получения практических результатов в сложных системах можно разработать модель использования закона Снеллиуса (например, для изучение электрического тока в грунтовых и водных электролитах).

Сначала заметим, что отношение sinα/sinφ для любого вещества является неотъемлемым свойством – таким как его температура кипения или плавления. «Любую придуманную модель распространения света (или электромагнитной энергии) можно будет испытать, выясняя вопрос, объясняет ли она второй закон преломления – закон Снеллиуса».

Особенности рассматриваемой системы

1. Грунтовую и водную среды принято

считать не изотропными и даже не анизотропными, а гиротропными, поэтому ε и μ принимать за const и равным единице.

2. Ток образуется одновременно и противополярными частицами и движется от анода к катоду в виде положительных частиц, а от катода к аноду – отрицательных частиц с разными скоростями.

3. Система подчиняется законам Ома и Джоуля-Ленца, т.е. «вся» электромагнитная энергия источника, постоянной или выпрямленной ЭДС, превращается в теплоту.

4. Поток энергии заряженных частиц, движущихся в противоположных направлениях, принимается за общий поток вектора Пойнтинга, в котором локализована энергия источника, который при взаимодействии со средой раздваивается на два потока, сложно взаимодействующих между собой, но обязательно в соответствии с законами сохранения баланса энергии, импульса и количества движения.

5. На границах анод-среда и катод-среда, под воздействием ЭДС источника образуются два двойных слоя, емкости которых зависят от величины ЭДС источника.

6. Потенциальная система защищаемого сооружения (катода) является гальваническим элементом (источником электромагнитной энергии) не ЭДС, а источником тока [1].

Выбор базовой модели. Наиболее простой и понятной исходной моделью, для получения количественных показателей на базе прямых измерений в системе анод-катод нами принята модель Снеллиуса-Максвелла: падения, преломления и отражения энергии, локализованной в пространстве вектором Пойнтинга. Вектор Пойнтинга, как выше было показано, включает в себя напряженность магнитного и электрического полей, характеристику его зависимости от изменения магнитной восприимчивости, диэлектрической постоянной и является законом сохранения энергии.

На рис. 1 представлено геометрическое построение, приводящее к закону Снеллиуса.

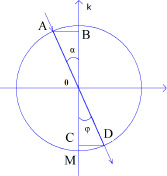
Геометрическое построение, приводящее к закону Снеллиуса

Здесь отношение хорд AB/AO = sinα, а СД/ОД = sinφ. Поскольку, АО и ОД есть радиус одной и той же окружности то:

где 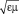, – показатель преломления, аналогично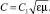

Методика исследования

1. Измерялась выпрямленная мощность P в цепи ваттметром при различных фиксированных значениях, возможных для данной установки токов I, измеряемых амперметром, устанавливаемых изменением напряжения по вольтметру U.

2. Заносились в журнал показания приборов (табл. 1) для каждого фиксированного режима источника.

Таблица 1

Экспериментальные данные для фиксированных напряжений от Umin до Umax

3. По выявленным автором формулам [2, 3]

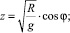
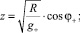
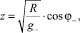
где Z = U/I+; 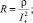; φ, φ+, φ– – углы преломления потоков движущихся частиц, определялись cosφ; cosφ+; и cosφ–, а также сумма углов φ = φ++φ– (табл. 2).

Приведенный расчет показывает (табл. 2), что:

1. Мощность, измеряемая ваттметром, равна мощности, равной произведению падения напряжения на ток, не измеряемый амперметром, а ток, определяемый суммой токов, образованных движением анионов и катионов в соответствии с законом Фарадея: I = P:U∙1,6∙10–19∙6,25∙1018.

2. При изменении уровня падения напряжения, измеряемого вольтметром, изменяются углы преломления энергий потоков движущихся частиц, направленных от анода к катоду и от катода к аноду.

3. При повышении уровня напряжения, приложенного к электродам, угол φ++ уменьшается, угол φ–- увеличивается, сумма углов при этом остается постоянной величиной и равной π/2.

4. Проводимости g+ и g– монотонно уменьшаются и в сумме составляют общую проводимость равную g. При g+ = g– ток в электролите равен нулю.

Таблица 2

Расчетные данные электронной и ионной проводимостей, углов преломления энергии от соответствующих сопротивлений и соответствующих падений напряжения на этих сопротивлениях

Библиографическая ссылка