Идемпотентная алгебра представляет собой область современной прикладной математики, связанную с изучением идемпотентных полуколец с операцией сложения. Несмотря на то, что идемпотентная алгебра является сравнительно молодой областью прикладных исследований, она уже нашла широкое применение в различных областях экономики, техники, управления, оптимизации и многих других [1-3].
Основным преимуществом идемпотентного подхода является возможность представления ряда нелинейных в обычном смысле задач их линейными в идемпотентном смысле аналогами, что приводит к упрощению их анализа, решения, интерпретации полученных результатов, а также программной реализации.
В прикладной математике и математическом моделировании применение идемпотентного подхода оправданно в ряде задач экономико-математического моделирования, в задачах с использованием графовых структур, при моделировании стохастических систем массового обслуживания [1].
Цель работы – исследование возможности применения идемпотентного подхода в задаче планировании производственного процесса.
При моделировании производственного процесса строится некоторая целевая функция (затрат, прибыли или проч.) вида:
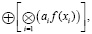
и решается оптимизационная задача в выбранном согласно прикладной области идемпотентном полукольце. Выделяют следующие идемпотентные полукольца [2]:
1) 
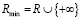с операциями 
, 
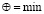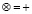и нейтральными элементами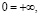 
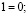
2) 
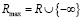с операциями 
, 
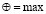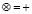и нейтральными элементами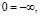 
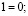
3) 
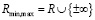с операциями 
, 
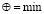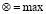и нейтральными элементами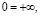 
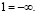
Рассмотрим постановку задачи моделирования и планирования производственного процесса и ее решение в идемпотентном полукольце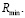 
Пусть имеется n видов сырья, которые должны использоваться в любом из m производственных процессов. Для всех процессов заданы нормы времени на потребление каждого вида сырья. Процесс остановится, если сырье хотя бы одного вида будет исчерпано.
Для каждого процесса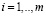 
введем обозначения:
yi – максимальная продолжительность процесса;
aij – среднее время потребления единицы сырья j
Для каждого вида сырья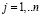 
определим величину 
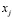– начальное количество сырья. Максимальная продолжительность процесса определяется равенством в полукольце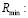 
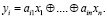
В векторных обозначениях имеем равенство:
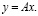(1)
Предположим, что для каждого процесса запланирована определенная продолжительность bi. Необходимо установить такой минимальный начальный запас сырья, чтобы при запуске любого из процессов обеспечить запланированную продолжительность процесса. Пусть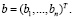 
Уравнение (1) имеет решение тогда и только тогда, когда 
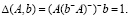При этом 
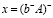– максимальное решение.
Была построена математическая модель производственного процесса прокатки сляба на непрерывном прокаточном стане («Стан-2000» на ОАО «Новолипецкий металлургический комбинат»). Основными ресурсами, используемыми на каждой стадии технологического процесса, являются топливо и электрическая энергия. В модель также были включены дополнительные потребности в ресурсах на каждой из технологических стадий производства. В результате решения задачи о планировании производства были получены приближенные решения в полукольце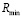 
, среди них выбрано оптимальное в смысле минимальной нормы невязки.
Выводы
Апробация данного подхода на ряде производственных процессов позволила прийти к выводу о том, что идемпотентная алгебра может быть использована в задаче планирования производства, реализация и непосредственные вычисления просты, однако существует ограничение на одновременное использование всех видов сырья в каждом из технологических процессов, нарушение которого моет привести к неразрешимости уравнения в полукольце Rmin. Данное ограничение сокращает область применения идемпотентного подхода в задаче планирования производственного процесса и требует дополнительных исследований в данном направлении.
Работа поддержана РФФИ, проект № 11-07-00580-а.
Библиографическая ссылка
Черных О.О. МОДЕЛИРОВАНИЕ ПРОИЗВОДСТВЕННОГО ПРОЦЕССА СРЕДСТВАМИ ИДЕМПОТЕНТНОЙ АЛГЕБРЫ // Международный журнал прикладных и фундаментальных исследований. 2013. № 10-2. С. 155-156;URL: https://applied-research.ru/ru/article/view?id=4101 (дата обращения: 11.05.2025).