Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Файлы
• Литература

Павлов А.М. 1

---

1 РГП на ПХВ «Восточно-Казахстанский государственный университет им. С. Аманжолова»

Статья в формате PDF

1035 KB

1.Вассерман А.А, Рабинович В.А. Теплофизические свойства жидкого воздуха иего компонентов.– М.: Изд. комитета стандартов, мер иизмерительных приборов при Сов. мин. СССР, 1968.– С. 240.

2.Френкель Я.И. Кинетическая теория жидкостей.– Л.: Наука, 1975.– С. 592.

В жидкостях наблюдается ближний порядок. Следовательно, молекулы или атомы совершают в основном колебательное движение около положения равновесия, которое время от времени меняется. Чтобы определить период и частоту колебаний необходимо найти потенциальную энергию молекулы, обусловленную её взаимодействием с ближайшими соседями. Для определения этой энергии воспользуемся моделью, аналогичной модели самосогласованного поля в атомной физике. Эта идея принадлежит Леннард-Джонсу и Девоншайру, и развита Я.И. Френкелем [2].

Суть этой идеи заключается в том, что задача о движении N взаимодействующих частиц заменяется задачей о движении каждой из них в поле, создаваемом остальными N-1 частицами. Поле, создаваемое этими N-1 частицами можно считать сферически симметричным, а сами частицы закрепленными в своих положениях равновесия, т.е. в узлах кристаллической решетки.

Получается, что каждый атом жидкости (или молекула) находится в сферической ячейке радиуса a, близкого к среднему расстоянию между соседними частицами в решетке с координационным числом ν и определяемого из условия, чтобы объём, приходящийся на одну частицу V/N, совпадал с тем, который соответствует кристаллическому состоянию.

Если считать атомы твёрдыми шариками с диаметром а, то при их плот ной упаковке в гранецентрированной кубической решётке с числом n=12 ребро ячейки равно 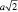и содержит 4 атома. Тогда объем, приходящийся на один атом

.

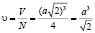В то время как объём сферической ячейки радиуса a равен 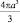, что несколько больше υ. Тем не менее, будем считать объём ячейки равным .

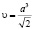Пусть молекула А зафиксирована в своём положении равновесия, а молекула В может занимать любое положение на сфере радиуса r<a, центром которой является точка О – положение равновесия молекулы В. Расстояние от А до О равно равновесному расстоянию между молекулами – a. Будем считать все молекулы неподвижными, кроме В, которая перемещается по указанной сфере. Точнее может занимать любое положение на этой сфере при колебаниях относительно точки О в усредненном поле сил остальных молекул. Таким образом, задача свелась к нахождению энергии молекулы В в этом усредненном поле, когда она отклонится от положения равновесия на расстоянии r.

Для определения указанной энергии воспользуемся потенциалом Леннарда-Джонса в виде:

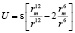, (1)

где rm – равновесное расстояние в этом потенциале, которое связано с диаметром молекулы соотношение: 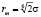или .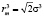

Расстояние rB можно выразить через a и r:

.

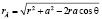После подстановки rB в (1) и интегрирования по θ от 0 до π, получаем:

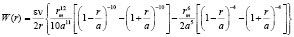, (2)

где n – число соседей у молекулы В. Разлагая выражения в круглых скобках в ряд по степеням r/a и ограничиваясь слагаемыми, содержащими r5/a5, будем иметь:

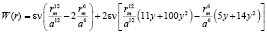, (3)

где 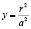. При r=0 получается энергия в состоянии равновесия, т.е. формула (1) при r=a:

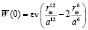. (4)

Тогда оставшаяся часть из (3) будет являться потенциальной энергией колебательного движения частицы В:

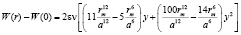. (5)

Отношение rm/a стоящее в круглых скобках можно заменить отношением собственного объёма атома или молекулы к объёму, приходящемуся на одну частицу. Из сказанного ранее следует, что собственный объём частицы равен

,

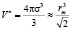а объём, приходящийся на одну частицу .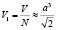

Отсюда

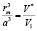. (6)

Поставляя это в (5), получим:

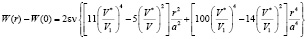. (7)

Как известно, вторая производная от потенциальной энергии по координате определяет коэффициент жёсткости молекулярных квазипружин С. В нашем случае

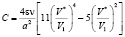. (8)

Чтобы С было положительным и не равнялось нулю, необходимо выполнение неравенства: rm>0,8768a или 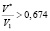. Обратное отношение 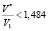. Это отношение меньше, чем отношение этих величин в критическом состоянии, равное .

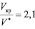Следовательно, при температурах гораздо ниже критических молекулы перестают колебаться, а совершают поступательное движение, как в газах. Эта температура, конечно, зависит от давления. Так у молекул аргона температура указанного перехода при давлении 5 бар равна 98К, а при 25 барах – 100К [1]. Получается, что при этих температурах в жидкостях происходит что-то вроде фазового перехода второго рода. Вроде ничего не меняется, кроме характера теплового движения. Однако характер теплового движения определяют окружающие молекулы. Следовательно, должно меняться число соседей и равновесное расстояние между молекулами, т.е. микроструктура жидкости. Теряется квазикристаллическое строение и жидкость становится аморфной. Если пренебречь нелинейным слагаемым в силе взаимодействия, т.е. второй квадратной скобкой в (7), то частота колебаний будет определяться выражением:

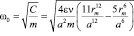. (9)

Как видно из (9) эта частота не зависит явно от Т, а зависит от числа соседей ν и отношения 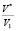. Однако и число соседей ν и указанное отношение являются функциями температуры. Следовательно, и ω0 будет функцией температуры.

Однако если учесть второе слагаемое в (7), то получается и явная зависимость частоты колебаний от температуры. Перепишем (7) в виде

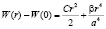, (10)

где С определяется выражением (8), а

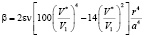. (11)

Определим сначала амплитуду колебаний, используя закон сохранения энергии:

.

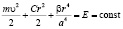При υ=0 смещение частицы равно амплитуде колебаний. Следовательно

,

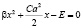где x=A2/a2. Решение этого уравнения будет:

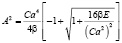. (12)

Как известно, среднее значение энергии молекулярного осциллятора равно kT. Кроме того, отношение 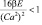. Так для аргона ε=120 при Т=85К и числе соседних молекул 6 это отношение равно 0,564. Следовательно, корень можно разложить в ряд и сохранить только первые два слагаемых. При этих условиях получаем

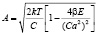
или при β=0

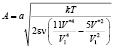. (13)

Если не считать зависимости ν и V1 от температуры, то A~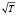. На самом деле и ν и V1 являются функциями Т, следовательно зависимость А(Т) носит более сложный характер. Если считать, что ν не зависит от Т, а V1~T (объёмное расширение при нагревании), то тогда амплитуда колебаний будет пропорциональна Т3/2.

Перейдем к определению периода и частоты колебаний. Поскольку не удалось свести интеграл 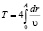к эллиптическому, будем определять частоту колебаний из дифференциального уравнения движения атома или молекулы:

.

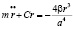Перепишем его в виде

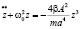, (14)

где z=r/A.

Поскольку однородное уравнение имеет решение

,

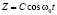то решение неоднородного уравнения будем искать в виде

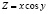. (15)

К этому условию добавим еще одно

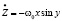. (16)

С помощью уравнений (14)–(16) получается следующая система уравнений для x и y:

;

.

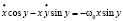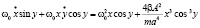Разрешая эту систему уравнений относительно 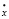и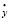

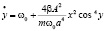. (17)

Поскольку отношение амплитуды колебаний к расстоянию между частицами мало, т.е. А/a«1, то система уравнений (17) имеет малый параметр. Это позволяет амплитуду х и фазу y искать в виде разложения по степеням этого параметра:

,

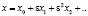
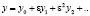где .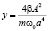

Тогда для х и у получается следующая система уравнений:

; ; …

; ; …

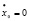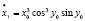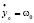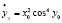Учитывая малость ε, можно ограничиться этим приближением. Примем, что в начальный момент частица отклонена на максимальное расстояние, т.е. х0=1. Тогда получаем:

;

.

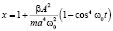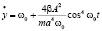Последнее равенство определяет частоту колебаний:

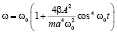. (18)

Если сюда подставить значение амплитуды из (12) и усреднить 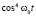, то получим:

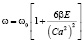. (19)

Среднее значение энергии колебательного движения молекул, как известно, равно kT, следовательно (19) можно переписать в виде

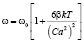. (20)

Отсюда видно, что средняя частота колебаний увеличивается при увеличении температуры.

Итак, из наших расчётов следует:

1. Жидкости, имея вдалеке от точки кипения квазикристаллическую структуру, при определенной температуре, зависящей от давления, теряют её и переходят в аморфное состояние.

2. Внешнее давление способствует сохранению квазикристаллической микроструктуры жидкости, так как при увеличении давления температура перехода увеличивается.

3. Амплитуда и частота колебаний молекул в жидкости зависят от температуры. Амплитуда колебаний пропорциональна Т1/2, а частота – пропорциональна Т.

Библиографическая ссылка