Колебания трактора, возникающие при выполнении машинно-тракторным агрегатом технологических операций, связанных с выращиванием сельскохозяйственных культур, приводят к нарушению агротехнических требований для создания благоприятных условий произрастания растений (глубина обработки почвы, заделки семян и др.), снижают тягово-сцепные свойства трактора, ухудшают условия труда водителя, уменьшают его работоспособность, оказывают вредное влияние на работу механизмов, вызывая их преждевременный износ. Колебания тракторов при их работе приводят к переуплотнению почв, а это вызывает снижение плодородия почв и, вследствие этого, урожайности полевых культур.
Необходимо повышать плавность хода тракторов. Весьма значительные исследования колебаний тракторов выполнены целым рядом авторов [1–6]. В то же время остается еще много нерешенных вопросов.
Важную роль в разработке мер по повышению плавности хода тракторов должны сыграть методы расчета показателей, характеризующих колебания тракторов. Эти методы нужно создавать на основе результатов углубленных исследований упругих или вязкоупругих свойств подвесок тракторов и реологических свойств почв. В настоящее время таких методов имеется мало.
Цели данной работы состояли в следующем: применить предложенную в работе [7] математическую модель задачи определения вертикальных колебаний передней и задней осей колесного трактора с вязкоупругой передней подвеской, работающего на уплотняющейся связной почве и метод расчета вертикальных колебаний такого трактора; найти этим методом на основании полученных нами экспериментальных данных, показатели, характеризующие колебания трактора Т150-К; по разработанным нами компьютерным программам выполнить расчеты, позволяющие оценить количественно влияние основных факторов (частоты колебаний возмущающих сил, амплитуды возмущающих сил, коэффициент демпфирования амортизаторов подвески) на вынужденные колебания трактора; исследовать взаимно независимые колебания передней и задней осей трактора и выявить некоторые условия их возникновения.
Материалы и методы исследования
Объектом исследования являлся колесный трактор с вязкоупругой передней подвеской, работающий на уплотняющейся связной почве. В работе использованы полученные нами ранее экспериментальные данные о вязкоупругих свойствах и зависимости от глубины плотности исследованных нами супесчаных почв. Выполнены компьютерные эксперименты по разработанным нами программам.
Результаты исследований и их обсуждение
Математическая модель задачи определения вертикальных колебаний осей колесного трактора с вязкоупругой передней подвеской при работе трактора. Метод расчета вертикальных колебаний трактора
Пусть машинно-тракторный агрегат, состоящий из трактора с полужесткой подвеской и агрегатируемой им машины работает на уплотняющейся связной почве. При полужесткой подвеске задние колеса трактора не подрессорены [4]. Оба моста трактора ведущие. Подвеска переднего моста является вязкоупругой. Она содержит упругие элементы, представляющие собой две продольные полуэллиптические рессоры, и вязкие элементы – два гидравлические амортизатора, предназначенные для снижения колебаний. Такой подвеской в числе некоторых других тракторов снабжен трактор Т-150К.
Поверхность почвы примем горизонтальной. Основное влияние на плавность хода трактора оказывают колебания поступательные вертикальные и угловые продольные. Угловые продольные колебания выражаются аналитически через поступательные вертикальные [4].
Как и в работе [7] введем вертикальные оси координат x и y. Ось x проходит через вертикальный диаметр наружной окружности переднего колеса, ось y – через вертикальный диаметр наружной окружности заднего колеса одной и той же стороны трактора (например, правой по ходу движения). Начало каждой из осей расположим на опорной поверхности. Вертикальные отклонения от положения равновесия точек трактора при колебаниях его передней и задней осей равны соответственно x и y.
Приведенная жесткость упругого элемента передней подвески равна
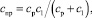 (1)
(1)
где ср – жесткость рессоры; c1 = G1/f1 – жесткость шины переднего колеса; G1– вертикальная нагрузка на ось переднего колеса; f1 – вертикальное перемещение его оси [2, 4].
Амортизатор оказывает вязкое сопротивление R = ηx′, где η – коэффициент демпфирования.
Для нахождения колебаний x и y передней и задней осей трактора составим, воспользовавшись принципом Даламбера, систему двух дифференциальных уравнений:
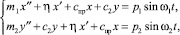 (2)
(2)
где c2 = G2/f2 – жесткость шины заднего колеса; G2 – вертикальная нагрузка на ось заднего колеса; f2 – вертикальное перемещение его оси; mj – подрессоренные части массы трактора, приходящиеся соответственно на его переднюю и заднюю полуоси (здесь и далее для переднего колеса j = 1, а для заднего – j = 2); pj– амплитуды колебаний вертикальных реакций опорного основания (возмущающих сил); ωj– круговые частоты колебаний возмущающих сил; t – время. Величины fj находим по формуле из работы [8]. Неподрессоренные массы трактора (массы колес) приближенно не учитываем, так как они существенно меньше подрессоренных [2, 4].
Вертикальные колебания передней и задней осей трактора определим как решение следующей задачи: найти частное решение системы уравнений (2), удовлетворяющее начальным условиям:
1) 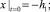 2)
2) 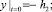
3) 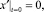 (3)
(3)
где h1 и h2 – полная осадка почвы соответственно под передним и под задним колесом трактора без учета влияния колебаний трактора.
Общее решение системы неоднородных дифференциальных уравнений (2) равно сумме общего решения (X, Y) системы однородных дифференциальных уравнений, соответствующей системе (2), и какого-либо ее частного решения (xч, yч): x = X + xч; y = Y + yч. В случае малого коэффициента η в [7] получили:
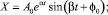
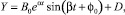 (4)
(4)
где 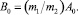 Круговая частота колебаний β и коэффициент α равны:
Круговая частота колебаний β и коэффициент α равны:
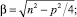 (5)
(5)
α = –p/2, (6)
где p = η/m1; (7)
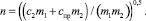 (8)
(8)
Величина p < n (если это соотношение выполняется, то коэффициент η считают малым).
Угол φ0– начальная фаза колебаний.
Частное решение системы (2) отыскиваем в виде:
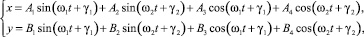 (9)
(9)
где Aj и Bj (j = 1, 2, 3, 4) – амплитуды слагаемых гармоник; γ1 и γ2 – сдвиги фаз колебаний осей по отношению к фазам возмущающих сил. Нашли γ1 = γ2 = π; это означает, что каждая из возмущающих сил и вызванные ею колебания оси находятся в противоположных фазах. (Этот результат аналогичен приведенному в работе [9] для случая исследования колебаний одного линейного осциллятора). Выполнив преобразования получили систему 8-и линейных алгебраических уравнений с 8-ю неизвестными Aj и Bj. Полученная система уравнений является совместной и определенной. Решая ее, находим Aj и Bj.
Используя общее решение системы (2) и начальные условия (3), нашли формулы для определения A0, φ0 и D.
Таким образом, вертикальные колебания передней и задней осей трактора, удовлетворяющие начальным условиям (3), описываются формулами:
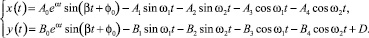 (10)
(10)
Первые слагаемые алгебраических сумм, стоящих в правых частях формул (10), характеризуют свободные (собственные), а остальные – вынужденные колебания осей трактора. Так как α < 0, то A0eαt → 0 и B0eαt → 0 при t → ∞, то есть свободные вертикальные колебания осей трактора со временем затухают. Круговые частоты вынужденных колебаний осей равны частотам ω1 и ω2 возмущающих сил. Вынужденные колебания, в отличие от свободных, со временем не затухают.
На основе выполненного математического моделирования нами предложен метод расчета вертикальных колебаний передней и задней осей трактора при его работе и разработаны компьютерные программы, позволяющие реализовать этот метод [7]. Для выполнения расчетов этим методом необходимо располагать данными о закономерностях деформирования почвы, эластичных колес трактора, а также его подвески.
В данной работе использованы результаты наших предыдущих исследований. Расчеты выполняли по разработанным нами компьютерным программам Soil, Modul E, Shina, Tractor и стандартной программе SGWIN 1.1. Результаты наших предыдущих исследований позволяют найти по приведенным выше формулам данные о колебаниях трактора. Помимо названных выше и примененных в представленной работе компьютерных программ, разработана и применена для выполнения расчетов компьютерная программа Amplitude.
Приняли, что верхний деформирующийся слой почвы, распространенный на глубину H, расположен на практически недеформирующемся основании. Поверхность почвы горизонтальна. Зависимость плотности ρ верхнего слоя почвы до проходов трактора от глубины z приняли квадратичной:
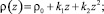
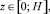 (11)
(11)
где k1 и k2 ≠ 0 – коэффициенты; ρ0 – свободный член, соответствующий ρ(0) (при z = 0). Зависимость (11) получена в результате статистической обработки экспериментальных данных [10, 12, 13].
При качении колес почва деформируется по гармоническому закону. Экспериментально подтверждено [10–13], что исследованные уплотняющиеся почвы в рассмотренных интервалах значений ρ и влажности w являются вязкоупругими и при гармоническом законе деформирования их свойства адекватно моделируются для каждого фиксированного z дифференциальным уравнением
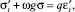 (12)
(12)
где σ – сжимающие напряжения, МПа; ε – относительные деформации сжатия; q, МПа и g – характеристики реологических (вязкоупругих) свойств почвы; ω – круговая частота гармонического процесса деформирования, c–1. Вязкоупругие свойства уплотняющихся почв моделировали этим уравнением.
Ход выполнения расчетов описан в работе [7]. В расчетах использовали экспериментальные данные, полученные нами в опытах, проведенных на поле экспериментального хозяйства РГАУ – МСХА им. К.А. Тимирязева [13]. Почва на этом поле – дерново-подзолистая супесчаная. Исследовали вязкоупругие свойства почвы, ее уплотнение колесами трактора МТЗ-82 на постоянном пути 30 м, влияние колебаний трактора на уплотнение почвы. Глубина распространения верхнего деформирующегося слоя почвы H = 0,9 м. Перед каждой серией экспериментов дважды выполняли дискование вспаханной почвы на глубину 0,3 м. Провели семь серий опытов. Каждая серия опытов состояла их шести последовательных проходов отдельно переднего и заднего колес трактора.
В данной работе в качестве исходной в каждом расчете применена полученная нами в результате статистической обработки экспериментальных данных квадратичная зависимость (11) плотности ρ верхнего слоя почвы до проходов колес тракторов от глубины z с параметрами: ρ0 = 1,2458 г/см3, k1 = 1,6287 г/(см3∙м), k2 = –1,0267 г/(см3∙м) (при w = 15 %). Корреляционное отношение для этой зависимости равно 0,9804.
Результаты компьютерных экспериментов по исследованию колебаний трактора Т-150К при работе на почве. Анализ полученных результатов
С использованием полученных экспериментальных данных о свойствах исследованной дерново-подзолистой супесчаной почвы выполнены компьютерные расчеты вертикальных колебаний x(t) и y(t) осей трактора Т-150К.
Трактор Т-150К тягового класса 30 кН с эксплуатационной массой 8400 кг имеет четыре ведущих колеса одинакового диаметра, радиус каждого колеса R = 0,7 мм; колеса снабжены шинами 21,3R24. Внутреннее давление воздуха в шинах передних и задних колес соответственно равно: 0,12 и 0,1 МПа. Массы, приходящиеся на переднюю и заднюю полуоси, соответственно равны: m1 = 2060, m2 = 1600 кг.
Подвеска трактора полужесткая, задний мост жестко соединен с рамой. Передние мосты подвешены на двух продольных полуэллиптических листовых рессорах. Подвеска трактора Т-150К снабжена также гидравлическими амортизаторами, работающими совместно с рессорами. Жесткость рессоры cp = 560 кН/м [1]. Коэффициент демпфирования амортизатора η = 300 Н∙c/м.
Рассматривали колебания, обусловленные неровностями пути. Согласно данным из работы [3] приняли, что неровности имеют равномерный закон распределения. Вынужденные вертикальные колебания трактора вызываются гармоническими колебаниями вертикальных реакций почвы на движущиеся колеса. Круговые частоты ωj колебаний возмущающих сил зависят от скорости v трактора и приведенных угловых скоростей колес [2, 4]. С увеличением v частоты ωj увеличиваются. Считая, что на участке поля длиной 1 м в среднем встречается одна неровность, приняли, что частоты ωj приближенно равны приведенным угловым скоростям колес. По результатам расчетов, выполненных по программе Tractor, вертикальных колебаний x(t) и y(t) осей трактора построены графики, характеризующие колебания осей. Полученные зависимости x(t) и y(t) удовлетворяют начальным условиям (3) рассмотренной задачи. На рис. 1 представлены построенные с помощью компьютерной программы Graph графики при v = 2 м/c (коэффициенты буксования колес δ1 = 0,1; δ2 = 0,09; p1 = p1 = 0,2 кН):
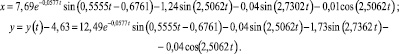 (13)
(13)
Нулевые линии графиков, характеризующих колебания обеих осей, совмещены.
Для этого выполнен параллельный перенос горизонтальной оси графика, описывающего колебания задней оси, на величину D. В результате расчетов получено, что в рассмотренных случаях свободные колебания затухают весьма быстро, время их затухания t ≤ 40 c. Выполненные расчеты подтвердили, что амплитуды вынужденных колебаний от начальных условий и времени не зависят, с течением времени они не затухают.
Помимо расчетов, выполненных по исходным данным полевых испытаний, нами проведено компьютерные эксперименты по исследованию влияния на вертикальные вынужденные колебания осей трактора Т-150К скорости трактора, частот возмущающих сил, амплитуд возмущающих сил, коэффициента демпфирования амортизаторов. Проведены однофакторные опыты и полные факторные компьютерные эксперименты. По результатам компьютерных экспериментов найдены по программе SGWIN 1.1 уравнения регрессии, характеризующие зависимости исследуемых показателей от названных факторов.
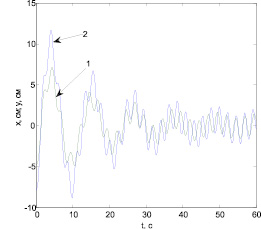
Рис. 1. Вертикальные колебания передней (1) и задней (2) осей трактора Т150-К при его движении по почве со скоростью v = 2 м/с
Однофакторные опыты по исследованию влияния на вертикальные колебания осей трактора скорости трактора, круговых частот возмущающих сил, амплитуд возмущающих сил, коэффициент адемпфирования амортизаторов. Для исследования влияния на вертикальные вынужденные колебания скорости трактора и амплитуд возмущающих сил провели семь однофакторных опытов, в которых принимали v = 0,9; 1,5; 2; 2,5; 3; 3,5 и 4 м/с. Определяемая при этих значениях v без учета влияния колебаний трактора полная осадка почвы под передним колесом соответственно равна h1 = 8,61; 5,98; 4,82; 4,01; 3,50; 3,12 и 2,88 см; под задним колесом соответственно равна h2 = 5,71; 4,01; 3,21; 2,73; 2,39; 2,14 и 1,95 см. Расчеты при каждом значении v выполнили при пяти различных значениях 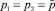 : 0,25; 0;2; 0;15; 0,1 и 0,05 кН.
: 0,25; 0;2; 0;15; 0,1 и 0,05 кН.
Суммарные амплитуды вынужденных колебаний As и Bs соответственно передней и задней осей трактора представляют собой суммы амплитуд гармоник, описываемых алгебраической суммой со второго по последнее из слагаемых в правых частях каждой из двух формул (10). Найдены уравнения регрессии, характеризующие зависимости As и Bs от v. При p2 = 190 Н, μ = 300 Н∙с/м получили: Bs = 4,17 – 3,32/v, см; корреляционное отношение равно 0,8251. Для исследования влияния круговой частоты возмущающей силы на Bs провели семь однофакторных опытов, в которых принимали ω2 = 1,35; 2,02; 2,73; 3,14; 3,45, 4.05 и 4,40 с–1. Найдены уравнения регрессии, характеризующие зависимости Bs от ω2. При p2 = 190 Н, μ = 300 Н∙с/м получили: Bs = 5,18 – 5б64/ω2, см. Корреляционное отношение этой зависимости равно 0,8873. Высокие корреляционные отношения во всех найденных уравнениях регрессии свидетельствуют о большой точности определения результативных факторов по этим уравнениям. Найдены уравнения регрессии, характеризующие зависимости амплитуд As и Bs вынужденных вертикальных колебаний осей трактора от амплитуд возмущающих сил (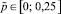 ). Получили, что As и Bs возрастают пропорционально возрастанию амплитуд pj. При v = 1,5 м/c, η = 300 Н∙с/м нашли следующие уравнения регрессии:
). Получили, что As и Bs возрастают пропорционально возрастанию амплитуд pj. При v = 1,5 м/c, η = 300 Н∙с/м нашли следующие уравнения регрессии: 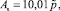 , см;
, см; 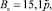 , см с коэффициентами корреляции 0,9856 и средними квадратическими отклонениями 0,0069 данных отдельных опытов от результатов расчетов по уравнениям регрессии. Получены данные, характеризующие влияние скорости трактора на изменение суммарных амплитуд As и Bs вертикальных вынужденных колебаний передней и задней осей трактора Т150-К и на изменение амплитуд их слагаемых гармоник (табл. 1).
, см с коэффициентами корреляции 0,9856 и средними квадратическими отклонениями 0,0069 данных отдельных опытов от результатов расчетов по уравнениям регрессии. Получены данные, характеризующие влияние скорости трактора на изменение суммарных амплитуд As и Bs вертикальных вынужденных колебаний передней и задней осей трактора Т150-К и на изменение амплитуд их слагаемых гармоник (табл. 1).
Таблица 1
Влияние скорости трактора на суммарные амплитуды вертикальных вынужденных колебаний передней и задней осей трактора Т150-К и на амплитуды их слагаемых гармоник
|
Амплитуды As и Bs и амплитуды слагаемых гармоник, cм |
v, м/с |
||||||
|
0,9 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
|
|
As |
1,36 4,90 |
0,54 2,00 |
0,34 1,25 |
0,21 0,81 |
0,17 0,63 |
0,15 0,54 |
0,14 0,53 |
|
Bs |
2,01 7,91 |
0,81 3,01 |
0,53 2,00 |
0,32 1,24 |
0,27 1,03 |
0,23 0,87 |
0,19 0,73 |
|
A1 |
1,21 4,39 |
0,52 1,89 |
0,34 1,24 |
0,21 0,77 |
0,17 0,62 |
0,15 0,53 |
0,14 0,52 |
|
A2 |
0,15 0,59 |
0,03 0,10 |
0,01 0,04 |
0 0,02 |
0 0,01 |
0 0 |
0 0 |
|
A3 |
0,07 0,24 |
0,01 0,03 |
0 0,01 |
0 0 |
0 0 |
0 0 |
0 0 |
|
A3 |
0,01 0,03 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
|
B1 |
0,11 0,39 |
0,11 0,07 |
0,03 2,01 |
0 0,01 |
0 0,01 |
0 0 |
0 0 |
|
B2 |
1,98 7,51 |
0,81 3,09 |
0,53 2,01 |
0,32 1,23 |
0,27 1,02 |
0,23 0,87 |
0,19 0,73 |
|
B3 |
0,11 0,39 |
0,01 0,05 |
0 0,02 |
0 0 |
0 0 |
0 0 |
0 0 |
|
B4 |
0,01 0,05 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
0 0 |
Примечание: в числителе – при 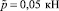 , в знаменателе – при
, в знаменателе – при 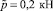 .
.
Полные факторные эксперименты по исследованию влияния на вертикальные вынужденные колебания осей трактора круговых частот возмущающих сил, амплитуд возмущающих сил, коэффициента демпфирования амортизаторов. Исследовали влияние на амплитуды As вертикальных вынужденных колебаний передней оси трактора круговой частоты возмущающей силы ω1, амплитуды p1 возмущающей силы, коэффициента η демпфирования амортизатора. Также исследовали влияние на амплитуды Bs вертикальных вынужденных колебаний задней оси трактора круговой частоты возмущающей силы ω2, амплитуды p2 возмущающей силы, коэффициента η демпфирования амортизатора. По разработанным нами компьютерным программам выполнили ряд расчетов, представляющих собой опыты в двух сериях (для переднего и для заднего колеса трактора) полных факторных компьютерных экспериментов типа N = 23, где N – число опытов в серии, 3 – число влияющих факторов, 2 – число уровней варьирования факторов [14]. Для каждого фактора выбрали основной уровень и по два равно от него отстоящих – нижний и верхний, которые соответственно равны: для ω1 = 1,36 и 3,81 с–1, для p1 = 50 и 250 Н, для η = 300 и 2800 Н∙с/м (для передней оси); для ω2 = 1,35 и 4,05 с–1, для p2 = 50 и 250 Н, для η = 300 и 2800 Н∙с/м (для задней оси). Ввели обозначения: 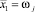 ,
, 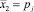 ,
, 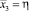 . Натуральные значения переменных
. Натуральные значения переменных 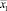 ,
, 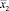 ,
, 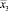 преобразованы в соответствующие кодированные по формуле
преобразованы в соответствующие кодированные по формуле
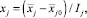 (14)
(14)
где j = 1, 2, 3 – номер фактора; 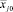 – натуральное значение основного уровня;
– натуральное значение основного уровня; 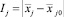 – интервал варьирования.
– интервал варьирования.
Матрица планирования эксперимента для передней оси представлена в табл. 2.
Таблица 2
Матрица планирования эксперимента для исследования влияния ω1, p1 и η на суммарные амплитуды вынужденных колебаний передней оси
|
Номер опыта |
|
|
|
|
1 2 3 4 5 6 7 8 |
1,36 3,81 1,36 3,81 1,36 3,81 1,36 3,81 |
50 50 250 250 50 50 250 250 |
2800 300 300 2800 300 2800 2800 300 |
Для каждого опыта, используя данные табл. 2, по компьютерной программе Tractor нашли амплитуды слагаемых гармоник A1, A4, A3, A4 для передней оси. Также для каждого опыта по программе Tractor нашли амплитуды слагаемых гармоник B1, B2, B3, B4 для задней оси. Так, в опыте № 5 вынужденные колебания осей описываются уравнениями:
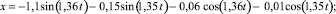
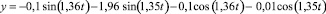 (15)
(15)
По компьютерной программе Graph 1 построили графики функций, описываемых уравнениями (15). На рис. 4 представлены графики, построенные по уравнениям (15). По этим графикам нашли суммарные амплитуды As и Bs. Аналогично построены графики и найдены амплитуды As и Bs для остальных опытов. Результаты расчетов использовали для получения уравнений регрессии амплитуд As и Bs от ωj, pj, η.
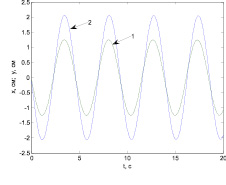
Рис. 2. Вынужденные вертикальные колебания передней (1) и задней (2) осей трактора Т150-К при его движении по почве с ω1 = 1,36 c–1, ω2 = 1,35 , p1 = p2 = 50 Н, η = 300 Н∙c/м
Уравнения регрессии в кодированных значениях переменных отыскивали в виде:
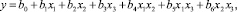 (16)
(16)
где y – значение результативного фактора; b0 – b6 – постоянные коэффициенты.
Получили выраженные в кодированных значениях переменных уравнения регрессии:
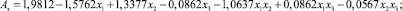 (17)
(17)
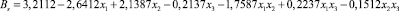 (18)
(18)
Коэффициенты множественной корреляции в уравнениях (17) и (18) равны 0,9955 и 0,9877, что свидетельствует о большой точности результатов расчетов по этим уравнениям.
В натуральных значениях переменных уравнения (17) и (18) преобразуются к виду:
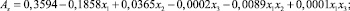 (19)
(19)
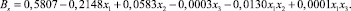 (20)
(20)
По уравнениям (17) и (18) видим, что основное влияние на амплитуды As и Bs оказывает круговая частота колебаний возмущающих сил ωj. Весьма значительно влияние амплитуд вынуждающих сил pj, а также произведения факторов ωj и pj. Роль коэффициента η демпфирования амортизаторов значительно меньше. Значительно также влияние произведения x1x2 факторов, характеризующее их совместное влияние. На амплитуду Bs существенно влияют произведения x1x3 и x2x3 факторов. Увеличении ωj и η приводит к уменьшению амплитуд As и Bs, а увеличение pj– к увеличению этих амплитуд. Влияние рассмотренных факторов на амплитуду Bs вынужденных колебаний задней оси больше, чем на амплитуду As вынужденных колебаний передней оси. Результаты полных трехфакторных экспериментов соответствуют результатам однофакторных опытов, проведенным на основании использования теоретических положений и результатам, полученным в исследованиях других авторов [2, 9, 15].
Применение полученных уравнений регрессии позволяет, варьируя в расчетах основные влияющие факторы ωj, pj и η, найти такие их значения, при которых вертикальные колебания трактора могут быть значительно уменьшены.
Результаты исследования взаимно независимых вертикальных колебаний передней и задней осей трактора
Из табл. 1 видно, что при увеличении v амплитуды As и Bs, а также Aj и Bj снижаются. Увеличение p1 и p2 вызывает возрастание As и Bs, а также Aj и Bj. На вынужденные колебания передней оси основное влияние оказывает слагаемое с амплитудой A1, это слагаемое имеет круговую частоту колебаний ω1. На вынужденные колебания задней оси основное влияние оказывает слагаемое с амплитудой B2, оно имеет круговую частоту колебаний ω2. С увеличением v число слагаемых гармоник уменьшается. При v ≥ 2,5 м/с вынужденные колебания каждой из осей состоят только из одной гармоники: с амплитудой A1– для передней и с амплитудой B2 – для задней оси. Это означает, что колебания осей становятся взаимно независимыми. При v ≥ 1,5 м/с и небольших p1 слагаемые с амплитудами A2, A3 и A4 значительно меньше, чем с амплитудой A1 и As ≈ A1. Также при v ≥ 1,5 м/с и небольших p2 слагаемые с амплитудами B1, B3 и B4 значительно меньше, чем с амплитудой B2 и Bs ≈ B2. Это показывает, что при v ≥ 1,5 м/с и небольших p1 и p2 колебания осей являются практически взаимно независимыми.
Пусть вертикальные колебания передней и задней осей трактора являются взаимно независимыми. При этом колебания передней оси моделируются дифференциальным уравнением
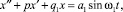 (21)
(21)
где p определяется формулой (7),
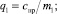 (22)
(22)
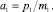 (23)
(23)
Общее решение уравнения (21) имеет вид
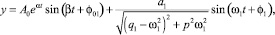 (24)
(24)
где
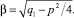 (25)
(25)
Первое слагаемое суммы, стоящей в правой части уравнения (24) характеризует свободные (собственные) колебания передней оси, а второе – ее вынужденные колебания. Угол φ01 – начальная фаза свободных колебаний, угол φ1 – начальная фаза вынужденных колебаний передней оси. Первое слагаемое названной суммы описывает затухающие колебания; при увеличении t оно убывает (так как α < 0), и, следовательно, через некоторый промежуток времени главное значение приобретает второй слагаемое, описывающее вынужденные колебания. Частота ω1 этих колебаний равна частоте вынуждающей силы a1sinω1t. Амплитуда вынужденных колебаний тем больше, чем меньше p и чем ближе 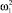 к q1.
к q1.
Нами исследованы зависимости амплитуд As = A1 вынужденных колебаний передней оси (независимых от колебаний задней оси) от частоты ω1 при различных значениях p1 = a1m1. Зависимости амплитуд вынужденных колебаний передней оси от ω1 характеризует формула
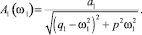 (26)
(26)
На рис. 3, а представлены полученные по формуле (26) кривые, характеризующие зависимости A1(ω1) амплитуд вынужденных колебаний передней оси трактора Т150-К при пяти значениях величин p1 = a1m1: 0,25; 0,2; 0,15; 0,1 и 0,05 кН и ω1 ∈ [0; 4] c–1. Из рисунка видно, что при увеличении ω1 от 0 до ≈ 0,2 c–1 значения A1 возрастают, достигая максимума, а при дальнейшем увеличении ω1 они убывают, асимптотически приближаясь к нулю. Однако следует отметить, что такие малые значения являются нереальными при работе трактора: диапазон скоростей переднего хода трактора Т150-К составляет 3,4–30,1 км/ч (больше 0,9 м/с), при этом ω1 > 1,34 c–1.
а б
Рис. 3. Зависимости амплитуд вынужденных вертикальных колебаний передней оси трактора Т-150К (независимых от колебаний задней оси) от круговой частоты вынуждающей силы: 1 – p1 = 0,25; 2 – p1 = 0,2; 3 – p1 = 0,15 ; 4 – p1 = 0,1; 5 – p1 = 0,05 кН
При всех реальных значениях ω1 (больших, чем 1,34 c–1) амплитуды вынужденных колебаний с увеличением частоты колебаний убывают; при ω1 ≥ 2 c–1 2 графики, полученные при различных p1 в масштабе рисунка практически совпадают. На рис. 3, б даны кривые, характеризующие зависимости A1(ω1)(, соответствующие графикам, представленным на рис. 3, а, при ω1 ∈ [2; 4]. На рис. 3 обозначены: ω1– через О1, A1 – через A1.
Нами исследованы также зависимости амплитуд As = A1 вынужденных колебаний передней оси (независимых от колебаний задней оси) от параметра
λ1 = ω1/β1, (27)
при различных значениях p1 = a1m1, где 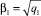 . Величина λ1 представляет собой отношение частоты возмущающей силы к частоте собственных колебаний трактора. Зависимости амплитуд вынужденных колебаний от величины λ1 характеризует формула
. Величина λ1 представляет собой отношение частоты возмущающей силы к частоте собственных колебаний трактора. Зависимости амплитуд вынужденных колебаний от величины λ1 характеризует формула
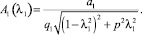 (28)
(28)
На рис. 4, а представлены полученные по формуле (28) кривые, характеризующие зависимости A1(λ1) амплитуд вынужденных колебаний передней оси трактора Т150-К при пяти значениях величин p1 = a1m1: 0,25; 0,2; 0,15; 0,1 и 0,05 кН и м/с. На рис. 4 обозначены: λ1– через L1, A1 – через A1.
а б
Рис. 4. Зависимости амплитуд вынужденных колебаний передней оси трактора Т150-К (независимых от колебаний задней оси) от λ1 = ω1/β1: 1 – p1 = 0,25; 2 – p1 = 0,2; 3 – p1 = 0,15 ; 4 – p1 = 0,1; 5 – 0,05
Вынужденные колебания задней оси трактора (независимые от колебаний передней оси) моделируются дифференциальным уравнением
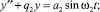 (29)
(29)
где q2 = c2/m2; (30)
a2 = p2/m2. (31)
Общее решение уравнения (29) имеет вид
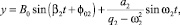 (32)
(32)
где
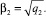 (33)
(33)
Первое слагаемое суммы, стоящей в правой части уравнения (32) характеризует свободные (собственные) колебания задней оси, а второе – ее вынужденные колебания. Угол φ02 – начальная фаза свободных колебаний. Исследование показало, что угол, соответствующей начальной фазе вынужденных независимых колебаний задней оси равен нулю. Как вынужденные, так и свободные колебания задней оси, независимые от колебаний передней оси, с течением времени не затухают. Вследствие этого колебания задней оси трактора больше колебаний его передней оси в течение всего времени работы трактора. Уменьшение амплитуды B0 собственных колебаний задней оси способствует снижению суммарной амплитуды ее колебаний.
Для трактора Т150-К при скорости v = 2 м/с, p2 = 0,25 кН вертикальные колебания задней оси являются независимыми от колебаний передней оси. Эти колебания при глубине h2 = 3,21 см описываются уравнением:
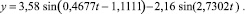 (34)
(34)
Нами проведено исследование зависимостей амплитуд Bs = B2 вынужденных колебаний задней оси (независимых от колебаний передней оси) от частоты ω2 при различных значениях p2 = a2m2. Эти зависимости характеризует формула
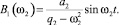 (35)
(35)
Вид графиков, построенных по формуле (35), соответствует виду графиков, представленных на рис. 3.
Выводы
1. На основе применения предложенной математической модели задачи определения вертикальных колебаний передней и задней осей колесного трактора с вязкоупругой передней подвеской разработан метод расчета вертикальных колебаний такого трактора. Разработаны позволяющие реализовать этот метод компьютерные программы.
2. Путем применения предложенного метод расчета с использованием полученных нами экспериментальных данных найдены показатели, характеризующие вертикальные колебания трактора Т150-К. Проведены однофакторные и полные трехфакторные компьютерные эксперименты, позволившие количественно оценить роль основных влияющих факторов (частот колебаний возмущающих сил, амплитуд возмущающих сил, коэффициента демпфирования амортизаторов подвески) в изменении показателей, характеризующих вынужденные вертикальные колебания трактора.
3. Использование полученных уравнений регрессии позволяет, варьируя в расчетах основные влияющие факторы ωj, pj и η, найти такие их значения, при которых вертикальные колебания трактора могут быть значительно уменьшены.
4. Для повышения плавности хода трактора необходимо:
– улучшать конструкционные свойства шин и показатели качества покрышек шин;
– снижать коэффициенты упругости шин;
– снижать коэффициенты жесткости шин;
– улучшать демпфирующие свойства шин и амортизаторов подвески передней оси.
5. Для снижения амплитуд вынужденных вертикальных колебаний осей трактора нужно увеличивать скорость трактора (в пределах, рекомендуемых агротехническими требованиями, предъявляемыми при возделывании различных сельскохозяйственных культур).
Для снижения частот вертикальных колебаний осей трактора нужно снижать скорость трактора (в допустимых пределах). В каждом конкретном случае необходимо находить оптимальное значение скорости.
6. Проведено исследование взаимно независимых колебаний передней и задней осей трактора. Исследование показало, что для трактора Т150-К в рассмотренных интервалах значений влияющих факторов при скорости трактора v > 1,5 м/с колебания осей становятся практически взаимно независимыми; при этом суммарная амплитуда колебаний задней оси увеличивается.
7. Полученные результаты могут быть использованы для выбора рациональных режимов работы машинно-тракторных агрегатов при выполнении технологических операций по возделыванию сельскохозяйственных культур.
Библиографическая ссылка
Золотаревская Д.И. ОЦЕНКА ВЛИЯНИЯ ОСНОВНЫХ ФАКТОРОВ НА КОЛЕБАНИЯ КОЛЕСНОГО ТРАКТОРА С ВЯЗКОУПРУГОЙ ПЕРЕДНЕЙ ПОДВЕСКОЙ // Международный журнал прикладных и фундаментальных исследований. 2013. № 10-3. С. 359-369;URL: https://applied-research.ru/ru/article/view?id=4209 (дата обращения: 14.03.2026).


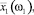 c–1
c–1
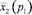 , Н
, Н
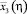 , Нм
, Нм