Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Глущенко А.Г. 1 Глущенко Е.П. 1

---

1 ГОУ ВПО «Поволжский государственный университет телекоммуникаций и информатики»

Рассмотрены эффекты фокусировки при прохождении света через пленки с керровской нелинейностью. Это позволяет использовать нелинейные пленки в качестве плоских линз. Показано, что особенности прохождения определяются геометрическими, физическими параметрами сред, а также амплитудой сигналов и распределением их интенсивности в поперечном к направлению распространения сечении.

Статья в формате PDF

404 KB

Плоские линзы

нелинейные пленки

керровская нелинейность

фокусировка

1. Веселаго В.Г. Электродинамика веществ с одновременно отрицательными значениями ε и μ // УФН. ‒ 1967. ‒ Т. 92. ‒ № 3. ‒ С.517.

2. Шевченко В.В. О сверхфокусировке плоской линзы из отрицательного материала // Журнал радиоэлектроники. № 6. – 2007.

3. Aieta F. et a. Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurface s// Nano Lett. – 2012. V.12 (9). – P. 4932–4936.

4. Pendry J.B. Negative refraction makes a perfect lens // Phys. Rev. Lett. – 2000. – 85(18). – P. 3966–3969.

Плоским линзам последнее время уделяется повышенное внимание в связи с потенциальной возможностью с помощью этих линз избежать абберационных искажений и реализовать свойства сверхразрешающей способности [1-4]. В литературе рассматриваются три способа фокусировки: неоднородного по радиусу распределения плотности среды, использование оптически отрицательных сред, использование искусственно-неоднородной среды. Неоднородность плотности среды с требуемой для оптического диапазона точностью наиболее простое, но технологически не реализуемое решение. Плоская (с плоскими границами) линза из материала с отрицательными диэлектрической и магнитной проницаемостями (оптически отрицательные среды), в частности, с равными по величине и разными по знаку по отношению к проницаемостям внешней среды, впервые была рассмотрена в работе [1], где дана геометрооптическая теория такой линзы. В статье [4] было заявлено, что такая линза обладает свойством сверхразрешения малых объектов, то есть способностью различать изображения объектов, размеры которых и расстояния между которыми меньше длины волны излучения. В статье [2] было показано, что бесконечная в поперечном направлении плоская линза из оптически отрицательной среды переводит поле точечного источника в точечное изображение независимо от длины волны излучения и обладает свойством сверхфокусировки. В [3] сообщается о создании плоской линзы по другой технологии. Вместо фазовых задержек отдельных лучей при прохождении света через всю толщину материала можно создать мгновенные фазовые сдвиги для отдельных лучей прямо на поверхности линз. Линза миллиметрового размера толщиной 60 нанометров изготовляется из кремния. Поверхность покрывается нанометровым слоем золота, из которого вытравливаются частицы – антенны нужной формы, которые при взаимодействии с электромагнитным излучением и располагаются концентрическими кругами. Антенна каждой формы реагирует с электромагнитным излучением на разной длине и создаёт фазовую задержку прямо на поверхности линзы. Массив наноантенн, называемый метаповерхностью, может быть настроен на длину волны простым изменением размера, угла и расстояния между антеннами. В сообщении предлагается делать такие линзы для диапазона от 1000 нм до 1 мм соответствующим подбором размеров и расстояний между антеннами. Видимая область не попадает в этот диапазон. Все эти способы связаны со сложностью технологий, из-за использования резонансных элементов узкополосны, не допускают возможности перестройки при изменении параметров излучений.

Модель плоской линзы. Здесь мы рассмотрим другую возможность управления локальными значениями показателя преломления самим оптическим сигналом с помощью пленки диэлектрика с керровской нелинейностью. Использование самого сигнала для управления его параметрами дает возможность создать управляемую легко перестраиваемую оптику, чем выгодно отличается от попыток решения проблемы фокусировки технологическими способами. Рассмотрим падение ограниченного в поперечном направлении луча света на пленку толщиной d с показателем преломления 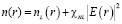( керровской нелинейность). Распределение поля по поперечному радиальному направлению неоднородное и описывается функцией E(r). За счет зависимости показателя преломления от интенсивности сигнала по поперечному сечению, пленка приобретает линзоподобные свойства: собирающей линзы при dn(r=0)/dr>0 и рассеивающей линзы при dn(r=0)/dr<0. Фазовый набег при неизменной толщине пленки зависит от расстояния до центра (рис. 1) из-за неоднородного распределения энергии в поперечном лучу сечении.

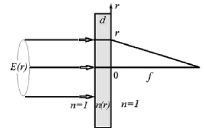
Рис. 1. Фокусировка луча при прохождении через пленку с керровской нелинейностью

Основные уравнения и результаты. Условием максимума в фокусе при сложении параллельных лучей, падающих на поверхность плоского слоя, является компенсация разности хода лучей в области после пленки их задержкой из-за различия скоростей лучей в различных областях области пленки. Условие фокусировки (интерференционного максимума для всех параллельных лучей, рис. 1) имеет вид:

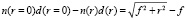, (1)

где f – фокусное расстояние.

Уравнение (1) показывает возможность различных способов фокусировки: 1) за счет изменения толщины пленки d(r). Использование неоднородности толщины слоя для фокусировки дает нам хорошо известную линзу,

2) за счет подбора радиальной неоднородности показателя преломления n(r). Использование искусственно создаваемой неоднородности показателя преломления n(r) дает возможность создать плоские неискажающие линзы толщиной в несколько десятков нанометров, однако стало возможным только в последнее время за счет использования современной нанотехнологии [4];

3) за счет нелинейности показателя преломления, зависящего от уровня сигнала, в свою очередь зависящего от r, в частности, при керровской нелинейности .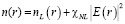

Соотношение (1) может использоваться для расчета функции распределения показателя преломления пленки, 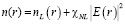, распределения поля E(r) или профиля толщины слоя диэлектрика d(r), обеспечивающих фокусировку луча за счет одного из этих параметров или комбинированного изменения параметров. Рассмотрим возможность создания радиальной неоднородности показателя преломления n(r) за счет эффекта Керра, радиальной неоднородностью интенсивности поля в поперечном сечении луча 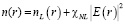. Пусть имеем плоский слой толщиной d=const (линейная часть показателя преломления предполагается постоянной, 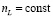), характеризуемый нелинейностью показателя преломления 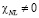. Найдем распределение поля E(r), при котором слой приобретает свойства собирающей линзы.

При параметре нелинейности 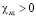фокусировка параллельного пучка света возможна при амплитуде волны в центре пучка, удовлетворяющей условию:

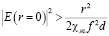. (2)

Таким образом, фокусировка имеет пороговое значение. При заданной интенсивности поля в центре пучка 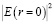фокусировка становится возможной при толщине пленки, удовлетворяющей условию:

.

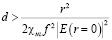Положение фокуса плоской линзы зависит от толщины слоя и интенсивности пучка :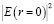

.

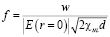Необходимая для фокусировки функция распределения поля определяется выражением:

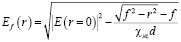. (3)

С учетом того, что фокусное расстояние обычно существенно больше радиуса пучка f>>r функция распределения поля может быть представлена в виде:

.

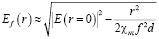Характер требуемой для точной фокусировки функции распределения поля по сечению показан на рис. 2. Здесь же для сравнения приведено распределение поля в гауссовом пучке.

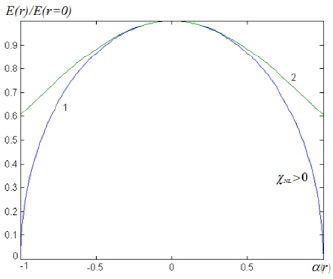
Рис. 2. Нормированная, обеспечивающая фокусировку функция распределения поля по радиусу (1) и функция, описываемая распределением Гаусса (2), .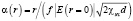

Точность фокусировки определяется точностью обеспечения необходимой функции распределения поля Ef(r)(3). При отклонении распределения поля от Ef(r) область фокусировки расплывается. Продольное распределение интенсивности поля на фокусном расстоянии зависит от степени отклонения реального поперечного распределения интенсивности от функции Ef(r).

Радиус пучка, обеспечивающий фокусировку, определяется соотношением:

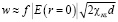
и пропорционален толщине слоя d, f, 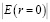. При заданной ширине пучка света w с ростом интенсивности поля уменьшается фокусное расстояние плоской линзы f, т.е. рост интенсивности поля увеличивает фокусирующие свойства плоской линзы. При коэффициенте нелинейности 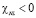слой приобретает свойство рассеивающей линзы.

Выводы. Сопоставление функций распределения поля в пучке необходимого для точной фокусировки и естественного для многих источников излучения гауссова распределения поля показывает, что основное различие наблюдается в периферийных областях пучка (r>0,5 w). При использовании источников с гауссовым распределением поля в пучке фокусировка будет «размытой». Ситуация аналогична размытости области фокусировки собирающих линз из-за погрешностей изготовления поверхностей линз. Для улучшения фокусировки требуется корректировка гауссового распределения интенсивности поля путем подавления периферийной области пучка. Очевидно, это технически намного проще реализовать, чем повышать требования к точности изготовления профилей поверхностей собирающих линз. Отметим, что соотношение (1) позволяет найти распределение интенсивности, необходимое для обеспечения свойств собирающей линзы для слоя с другими типами нелинейности показателя преломления.

Библиографическая ссылка