Простые числа приобретают особую важность в теории чисел в силу «фундаментальной теоремы арифметики», гласящей, что каждое составное число может быть представимо одним и только одним способом в виде произведения простых множителей [3, 7].
Первая теорема, утверждающая существование бесконечного множества простых чисел, была доказана уже Евклидом в «Началах», в книге 9, предложение 20 [3, 7].
Под критерием простых чисел понимается теоретико-числовое свойство, которое присуще лишь простым числам и наличие которого может быть установлено независимо от предварительной проверки простого числа. Простым примером является соотношение:
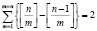, (1.1)
которое справедливо тогда и только тогда, когда n является простым числом. Так как слагаемые равны 1, если m делитель n, и равны нулю, если это не так, то сумма (конечная) представляет собой число d(n) делителей n, а равенство d(n)=2 характеризует простые числа. Естественно, формула (1), как и многие другие критерии, не пригодна для практических целей [6, 30].
Критерием числа на простоту является достаточное условие простоты числа. Кроме достаточных условий простоты числа также существуют необходимые условия.
Необходимым условием простоты числа является теоретико-числовое свойство числа присущее в большей степени простым числам, но это свойство могут иметь некоторые составные числа. Приведем примеры основных необходимых условий простоты числа:
1. Всякое простое число, большее 3, представимо в виде:
6k+1 или 6k–1. (1.2)
2. Если р – число простое, то верно сравнение:
р2–1≡ 0 (mod 24) (1.3)
3. Если р – число простое, то верны сравнения:
ар≡а (mod р), (a,p)=1, (1.4)
и ар-1≡1 (mod p), (a,p)=1, (1.5)
что означает, остаток от деления а р-1 на р равен 1, и соответственно остаток от деления ар на р равен а. (Малая теорема Ферма).
Существуют и другие необходимые условия простоты числа. Достаточным условием простоты числа является теоретико-числовое свойство числа присущее простым и только простым числам. Также приведем основные примеры этих условий, основанных на следующих теоремах:
1. Теорема Вильсона. Если p – число простое, то верно сравнение:
(p–1)!+1 ≡ 0 (mod p) (1.6)
Верно и обратное утверждение.
2. Теорема Лейбница. Если p – число простое, то верно сравнение:
(p–2)! – 1 ≡ 0 (mod p) (1.7)
Верно и обратное утверждение.
3. Теорема Серпинского. Если число вида p= 4k+1 и выполняется условие сравнения:
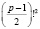+1 ≡ 0 (mod p), (1.8)
то число p – простое [5, 51-53].
Есть и другие теоремы, дающие условия простоты.
Проверка чисел на простоту на сегодняшний день является одним из самых актуальных задач в теории чисел, так как она связана с такой задачей как факторизация числа. Если проверка на простоту числа даст положительный ответ, то есть проверяемое число окажется простым, то операция факторизации числа отпадает. В случае отрицательного ответа встает задача нахождения нетривиальных делителей испытуемого числа.
Существует много тестов на простоту числа: тест Соловея-Штрассена, тест Миллера-Рабина, алгоритм Адлемана, Померанса, Румеля, алгоритм Ленстры, проверка числа теоремой Ферма, алгоритм Ленстры-Коена, алгоритмАдлемана- Хуанга (1972 г.), алгоритм Агравала, Кайалы, Саксены (2002 г.) и другие. Все вышеперечисленные методы и алгоритмы являются полиномиальными и потому являются вероятностными.
На сегодняшний день в криптографии в системе RSA открытым текстом используют многоразрядные числа, которые невозможно проверить на простоту числа со 100 процентной гарантией и невозможно разложить на простые множители (факторизация). Это связано с тем, что проверка больших чисел на простоту требует очень большое число операций, что не под силу даже суперсовременным компьютерам.
В этой статье мы хотим привести недостаток одного детерминированного алгоритма проверки числа на простоту, считающегося наиболее совершенным и потому имеющим широкое практическое применение в криптографии, а также представить новую теорему о критерии простого числа.
В книге Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. Москва, МЦНМО. 2003 г. В главе 1, §1.9 приведен детерминированный алгоритм проверки простоты на туральных чисел индийских математиков Агравала, Кайалы и Саксены (2002 г.),. Он имеет сложность O(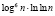
) арифметических операций (n – проверяемое число, c – некоторая абсолютная константа). Алгоритм основан на следующей теореме.
Теорема 1.71. Пусть p – нечетное натуральное число, a
Z(a,p)=1.
Число p является простым тогда и только тогда, когда
(x–a)p ≡ xp – a (mod p), [4, 48] (2.1)
Мы решили проанализировать эффективность этой теоремы.
Преобразуем левую часть сравнения (2.1) в следующий вид:
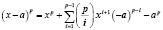. (2.2)
Если p – простое число, то верно сравнение:
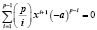(mod p), (2.3)
и сравнение (2.1) принимает вид:
– 
≡ 
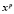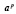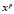– a (mod p), (2.4)
и последнее сравнение равнозначно малой теореме Ферма:
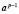≡ 1 (mod p). (2.5)
Теперь рассмотрим другой случай, когда p – составное число и притом является числом Кармайкла (псевдопростое числа), например, p1= 651=3∙11∙17, p2 = 2821=7∙13∙31, p3 = 10585=5∙29∙73, p4 = 15841=7∙31∙73 и так далее. Чисел Кармайкла бесконечно много [2, 703-722].
Экпериментальные вычисления показывают, что все эти числа пройдут тест на простоту по алгоритму индийских математиков и по малой теореме Ферма и дадут ложный ответ. Далее. При p – являющимся числом Кармайкла, естественно не найдутся числа q и k такие, удовлетворяющие условиям теоремы 1.71.
В связи с этой темой приводим новую теорему в теории чисел по критерию простого числа, являющейся банальным случаем, но не встречающейся в технической литературе.
Теорема о критерии простого числа. Автор – Ущтенов Есенбек Рискулович, авторское свидетельство № 128 от 14.02.2013 год, зарегистрированное в Комитете по правам интелектуальной собственности Министерства юстиции Республики Казахстан.
Теорема. Пусть n – натуральное нечетное число. Если выполняется условие (2.6), то верно утверждение, что n – простое число.
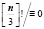(mod n) (2.6)
Искючения составляют только числа n=9 и n=25.
Доказательство.
Так как любое натуральное нечетное составное число может иметь наименьший делитель число 3, то наибольший делитель может быть равным числу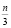 
. В случае, если это число имеет другие делители, то его делители будут находится в зоне между числами 3 и 
.
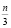Как известно, простое число n имеет два тривиальных делителя: 1 и самого себя n, и потому, не имея ни одного делителя от числа 3 и до числа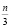 
, при делении этого простого числа на другие натуральные числа меньшие 
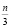, будут давать остатки от 1 до n–1.
На основании вышесказанного имеет место выражение (2.6).
Рассмотрим исключительные случаи.
Пример 1. Пусть n=9, тогда
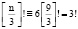. 1∙2∙3 = 6,
и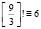 
(mod 9), (2.7)
Пример 2.
Пусть n=25, тогда
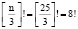1∙2∙3∙4∙5∙6∙7∙8 = 40320,
и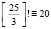 
(mod 25) (2.8)
Пример 3. Пусть n=49, тогда
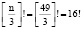. 1∙2∙3∙4∙5∙6∙7∙8∙9∙10∙11∙12∙13∙14∙15∙16,
и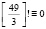 
(mod 25), (2.9)
потому что 7∙14=2∙49.
Из последнего примера видно, что последующие числа вида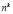 
, где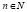 
, 
, 
, 
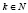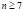, будут иметь результат:
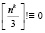(mod nk), (2.10)
и вследствие этого факта будут подчиняться условию (2.6), и соответственно, не будут являться простыми числами.
Теорема доказана.
Мы убедились, что теорема индийских математиков Агравала, Кайаны и Саксены 1.71 равнозначна малой теореме Ферма и поэтому не дает гарантированной простоты проверяемого числа и потому не эффективен.
Библиографическая ссылка
Акылбаев М.И., Уштенов Е.Р. НОВАЯ ТЕОРЕМА О КРИТЕРИИ ПРОСТОГО ЧИСЛА // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 1-2. – С. 255-257;URL: https://applied-research.ru/ru/article/view?id=4658 (дата обращения: 20.04.2024).