В основе теории электропроводности растворов электролитов, развиваемой в работах [1-5], лежит представление об энергии многочастичных взаимодействий через плазменное колебание зарядовой плотности. Существенным аргументом в пользу полученного уравнения для теоретических оценок электрических проводимостей могло бы быть установление его концептуального единства с теорией проводимости твердых тел. Возможный вариант решения данной проблемы и составляет предмет настоящей работы.
В качестве исходных предпосылок принимаются эквивалентные
представления плотности тока j через искомую проводимость λ, напряженность внешнего поля E, число Фарадея F, скорость движения зарядов ![]() , плотность носителей тока n0
, плотность носителей тока n0
![]() (1)
(1)
и четырехмерное уравнение движения в ковариантной форме
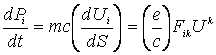 , (2)
, (2)
где ![]() - четырехмерная скорость;
- четырехмерная скорость; 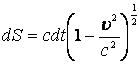 - пространственный интервал, при
- пространственный интервал, при ![]() , dS=cdt;
, dS=cdt; 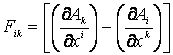 - антисимметрический ковариантный тензор электромагнитного
поля, как и четырехмерная скорость Ui, определяемая 4-радиусами-векторами
- антисимметрический ковариантный тензор электромагнитного
поля, как и четырехмерная скорость Ui, определяемая 4-радиусами-векторами ![]() и 4-векторами Ak и Ai; Pi=mcUi- 4-импульс.
и 4-векторами Ak и Ai; Pi=mcUi- 4-импульс.
Согласно равенству (1), основной проблемой для
нахождения λ является установление
скорости движения зарядов ![]() на основе уравнения
(2). Данное уравнение можно представить в развернутом виде, учитывая при этом,
что под дважды повторяющимися немыми индексами подразумевается суммирование:
на основе уравнения
(2). Данное уравнение можно представить в развернутом виде, учитывая при этом,
что под дважды повторяющимися немыми индексами подразумевается суммирование:
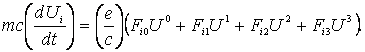 (3)
(3)
Для наглядности последующих рассуждений представим тензор в виде матрицы:
 , (4)
, (4)
в которой индекс i=0, 1, 2, 3 нумерует строки, а индекс k=0, 1, 2, 3- столбцы. Примем, что электрическое поле Ey направлено вдоль оси Y, а магнитное Hz- вдоль оси Z.
Уравнение (3) допускает раздельный анализ для
временной координаты i=0 и пространственной i=1, 2, 3. Для первого варианта уравнение (3) при 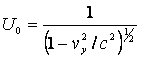 имеет вид
имеет вид
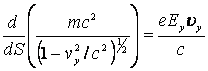 . (5)
. (5)
Из матрицы (4) видно, что при i=0 магнитное поле отсутствует вообще, а скорость ![]() направлена вдоль поля Ey. Известно, что для
направлена вдоль поля Ey. Известно, что для ![]() , где c- скорость света, возможно разложение величины U0, приведенной выше, в ряд по степеням
, где c- скорость света, возможно разложение величины U0, приведенной выше, в ряд по степеням ![]() , т.е. справедливо
, т.е. справедливо 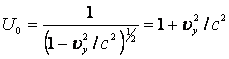 . Тогда для истинных траекторий движения зарядов в системе с
потенциалом
. Тогда для истинных траекторий движения зарядов в системе с
потенциалом ![]() , где ρ- плотность зарядов,
, где ρ- плотность зарядов, ![]() - элемент объема, а R- расстояние от точки наблюдения до dVв левой части уравнения (5) имеет место следующая аппроксимация
- элемент объема, а R- расстояние от точки наблюдения до dVв левой части уравнения (5) имеет место следующая аппроксимация
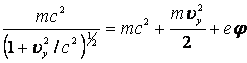 , (6)
, (6)
что формализует обобщенный импульс Pi [8, стр.90].
Далее, подставляя уравнение (6) в (5), при ![]() и последующем интегрировании
выражения
и последующем интегрировании
выражения
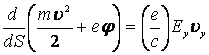
приходим к равенству следующего вида:
![]()
По определению ![]() есть работа
электрических сил. Тогда
есть работа
электрических сил. Тогда ![]() является внутренней
энергией [7], поскольку левая часть данного равенства представляет собой сумму
кинетической и потенциальной энергий. Отсюда, учитывая известное максвелловское
распределение по скоростям
является внутренней
энергией [7], поскольку левая часть данного равенства представляет собой сумму
кинетической и потенциальной энергий. Отсюда, учитывая известное максвелловское
распределение по скоростям 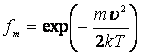 , получаем требуемое выражение для определения скорости движения
зарядов:
, получаем требуемое выражение для определения скорости движения
зарядов:
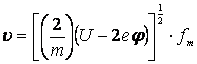 . (7)
. (7)
Детальное описание величин m, U, eφ и fm приведено в работах [1-5].
Следующий вариант анализа уравнения (3) связан с пространственными координатами i=1, 2, 3 при заданной геометрии сил. Выбранные направления электрических и магнитных полей Ey и Hz при i=2 приводят уравнение (3) и матрицу (4) к следующим видам:
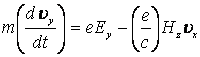 , (8)
, (8)
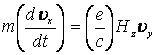 . (9)
. (9)
Здесь учитывается, что 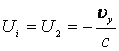 и
и ![]() , как ковариантные компоненты 4-скорости. Для решения
уравнений (8) и (9) умножают уравнение (8) на мнимую единицу i и складывают с
уравнением (9). При этом получается следующее равенство:
, как ковариантные компоненты 4-скорости. Для решения
уравнений (8) и (9) умножают уравнение (8) на мнимую единицу i и складывают с
уравнением (9). При этом получается следующее равенство:
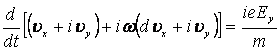 , (10)
, (10)
где ![]() - представляет собой частоту циклотронных колебаний.
- представляет собой частоту циклотронных колебаний.
Последующий анализ этого равенства дан в [8,стр.83].
Но если иметь в виду, что «компоненты скорости являются периодическими
функциями времени», то в (10) возможна стандартная аппроксимация ![]() . В этом случае после очевидных преобразований имеет место
выражение:
. В этом случае после очевидных преобразований имеет место
выражение:
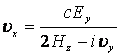 . (11)
. (11)
Подставляя данное значение ![]() в выражение (8),
получаем следующее равенство:
в выражение (8),
получаем следующее равенство:
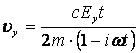 . (12)
. (12)
Таким образом, найденные значения скоростей (7) и (12) для временной и пространственных компонент уравнения (3), при их последующем использовании в уравнении (1), приводит к равенствам:
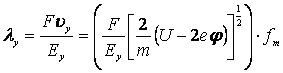 , (13)
, (13)
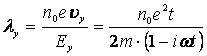 . (14)
. (14)
Очевидно, что при Hz=0, имеет место ω=0, и уравнение (14) трансформируется в классическую формулу Друде для проводимостей твердых тел [6, стр.271]. Наиболее существенным моментом в полученном уравнении (14) является то, что данное уравнение при iωt=1 обладает сверхпроводимостью [6, стр.449].
Таким образом, согласно уравнениям (13) и (14), искомая подвижность для растворов электролитов [4] определяется выражением
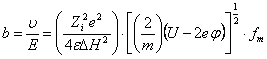 ,
,
а для твердых тел
 .
.
СПИСОК ЛИТЕРАТУРЫ
1.Балданов М.М., Мохосоев М.В. // ДАН СССР.-1985.- Т.284.- С.1384.
2. Балданов М.М., Мохосоев М.В., Танганов Б.Б. // ДАН СССР.-1989.-Т.308.-С.106.
3. Балданов М.М., Танганов Б.Б., Мохосоев М.В. //Журн. физ. химии.-1990.-Т.64.-С.88.
4. Балданов М.М., Танганов Б.Б., Мохосоев М.В.// Журн. физ. химии.-1991.-Т.65.-С.362
5. Балданов М.М., Танганов Б.Б. //Журн. физ. химии.-1992.-Т.66.-С.1084.
6. Киттель Ч. Введение в физику твердого тела. - М.: Наука,1978.-360 с.
7. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред.- М.: Госиздат. физ. мат. лит.,1959.-526 с.
8. Ландау Л.Д., Лифшиц Е.М. Теория поля.- М.: Наука, 1988.-683 с.
Библиографическая ссылка
Балданова Д.М., Балданов М.М., Танганов Б.Б. ПРОБЛЕМА ПРОВОДИМОСТЕЙ СИСТЕМ ЗАРЯДОВ В ГАЗОВОЙ ПЛАЗМЕ, ПЛАЗМЕ ТВЕРДЫХ ТЕЛ, РАСТВОРАХ ЭЛЕКТРОЛИТОВ И ТЕНЗОР ЭЛЕКРОМАГНИТНОГО ПОЛЯ // Международный журнал прикладных и фундаментальных исследований. 2010. № 1. С. 31-35;URL: https://applied-research.ru/ru/article/view?id=467 (дата обращения: 07.03.2026).

