Задача определения контактных напряжений имеет большое значение для расчета на прочность подшипников, зубчатых и червячных передач, шариковых и цилиндрических катков, кулачковых механизмов и других деталей машин.
Благодаря применению компьютерных технологий возможности расчета контактных напряжений в механизмах существенно расширились. Программа ANSYS поддерживает три контактные модели: узел с узлом, узел с поверхностью и поверхность с поверхностью. Каждый тип модели использует разные типы контактных элементов. Конечно-элементная модель распознает контактную пару по наличию контактных элементов, которые накладываются на те части модели, которые будут анализироваться на взаимодействие. Для формирования контактной пары эти элементы используют понятия «целевая поверхность»и «контактная поверхность». Для определения двумерных контактных пар используются конечные элементы TARGE169, CONTA172, для трехмерных контактных пар – TARGE170, CONTA174 [1].
Основные шаги для выполнения контактного анализа «поверхность к поверхности» изложены ниже:
- создание геометрической модели и сетки;
- проектирование контактной и целевой поверхностей;
- определение контактной и целевой поверхностей;
- установка реальных констант;
- установка необходимых граничных условий и опций решения;
- решение контактной задачи;
- анализ результатов.
С использованием данного алгоритма была разработана методика решения контактных задач на основе метода конечных элементов в ПК ANSYS [2,3]. Данная методика была опробирована на контактных задачах, решение которых получено классическими методами механики. Рассмотрим некоторые из них.
Задача контактного взаимодействия двух стальных шаров.
Рассмотрен случай возникновения контактных напряжений при взаимодействии стальных объектов (шара с шаром диаметрами 30 и 40 мм) при нагружении силой 1Н (вектор силы направлен от верхней точки меньшего шара и от нижней точки большего шара к точке касания шаров), как указано на рис. 1. Необходимо определить распределение давления в зоне контакта.
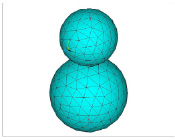
Рис. 1. Эскиз модели взаимодействия шара с шаром
Определим распределение контактных напряжений по поверхности шара. Согласно рис. 2 максимальное напряжение возникает в зоне соприкосновения шаров. С другой стороны, пятно контакта имеет форму эллипса, что еще раз доказывает соответствие компьютерного моделирования и реальное поведение объектов.

Рис. 2 Распределение контактного напряжения по поверхности
Проведено сравнение полученных результатов с аналитическим решением.
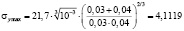 Па.
Па.
При моделировании были получены следующие результаты (рис. 3): нормальное напряжение по оси OY составляет 4,2354 Па, а следовательно погрешность составляет
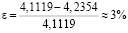 .
.
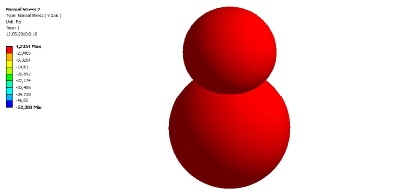
Рис. 3 Эпюра напряжений по оси OY
2. Задача взаимодействия двух цилиндров с параллельными осями.
Рассмотрим взаимодействие двух цилиндров с параллельными осями. Через два одинаковых стальных цилиндра длиной 200 мм передается равномерно распределенная нагрузка интенсивностью 500 кг/мм. Необходимо определить наибольшее напряжение по поверхности соприкасания, если диаметры цилиндров 70 мм.
Для расчета наибольшего напряжения необходимо построить модель цилиндров по исходным геометрическим параметрам. Произвести разбиение стальных цилиндров. Далее жестко закрепляем основания цилиндров и прикладываем равномерно распределенную нагрузку вдоль образующих цилиндров на боковых поверхностях. После разбиения размеры элементов на линии нагружения составляют порядка 9 мм, поэтому величина приложенной нагрузки будет рассчитана следующим образом
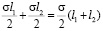
и составляет 4250 кг соответственно.
Результаты моделирования нагружения стальных балок представлены на рис. 4. По шкале максимальное напряжение по критерию фон Мизеса составляет около 100 кг/мм2.

Рис. 4. Распределение напряжений стальных балок
Для верификации модели решим данную задачу аналитическим способом. Первоначально приведем все исходные данные к международной системе единиц. При сжатии двух цилиндров радиусами R1 и R2, загруженных нагрузкой, равномерно распределенной по длине цилиндров, интенсивностью P, наибольшее напряжение будет определяться по формуле:
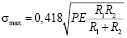 ,
,
(если цилиндры сделаны из материала с коэффициентом Пуассона 0,3 и модулем упругости E). Тогда
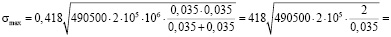
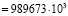 (Па) ≈
(Па) ≈ 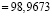 (кг/мм2).
(кг/мм2).
Полученный расчетный результат 989673·103Па и результат автоматизированного анализа в программном комплексе 100 кг/мм2 (в системе СИ 981000·103 Па) имеют небольшое расхождение 0,8 %.
Несмотря на то, что максимальные напряжения достаточно велики, это не означает разрушение материала в зоне контакта.
Полученные результаты работы могут использоваться для решения различных задач механики сплошных сред.
3. Контакт деформируемой модели с недеформируемой поверхностью
В качестве объектов исследования рассмотрены резиновый кубик и стальное основание (рисунок 5. Сверху кубик подвергается давлению. Необходимо определить напряжения и деформации кубика. Стальная форма принята абсолютно жесткой.
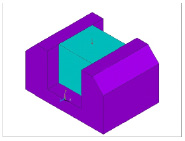
Рис. 5. Деформируемый кубик в жесткой форме
Жестко закрепляем основание формы, задаем в качестве контактных поверхностей – нижнюю грань резинового кубика и соприкасающуюся грань стальной недеформируемой формы (рис. 6).
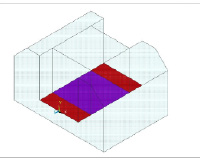
Рис. 6. Контактная пара
Анализируя полученные результаты, видно, что максимальные напряжения возникают на гранях резинового кубика, что соответствует действительности. Результаты моделирования представлены на рис. 7.
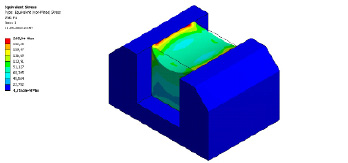
Рис. 7. Распределение контактных напряжений
Результаты проведенных исследований показали, что даже в зоне контакта возникают значительные напряжения, превышающие предел допустимых. Природа этого явления заключается в высоком уровне концентрации напряжений около нагруженного отверстия, где в зоне максимальных окружных напряжений имеет место коррозия трения, связанная с механическим истиранием поверхностей.
Таким образом, предложенная методика компьютерного анализа контактных напряжений является еще одним шагом на пути к точному моделированию деталей машин.
Библиографическая ссылка
Тутанов С.К., Даненова Г.Т., Коккоз М.М. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ КОНТАКТНЫХ НАПРЯЖЕНИЙ // Международный журнал прикладных и фундаментальных исследований. 2014. № 4. С. 36-39;URL: https://applied-research.ru/ru/article/view?id=5066 (дата обращения: 03.03.2026).

