Ранее в работе [2] было рассмотрено аналитическое описание распространения новшеств с использованием стохастической фрактальной клеточной модели. При этом было установлено, что распространение новшеств (новые технологии, потребительские товары, идеи) происходит в условиях существования соответствующих прототипов, новшества могут либо победить прототипы в конкурентной борьбе, либо нет, эта конкурентная борьба может происходить с различной степенью жесткости.
При описании распространения новшеств в некоторой абстрактной среде математическая модель должна быть не только достаточно общей, чтобы быть способной описать особенности любой конкретной среды, но и быть практически полезной и реализуемой с помощью средств вычислительной техники [2-3].
В качестве простейшего случая рассмотрим систему уравнений
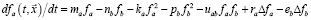, (1)
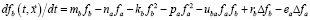. (2)
Точку насыщения можно найти, приравняв левую часть уравнений нулю и вычеркнув члены с пространственными производными.
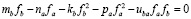, (3)
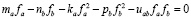. (4)
Вычтя из (3) умноженное на ka/pa уравнение (4), мы получаем линейное по fa уравнение. Выразив тогда fa через fb и подставив в (4), мы получим нелинейное уравнение одной неизвестной, которое легко может быть решено численно. С другой стороны, рассматривая взаимодействие между двумя распространяющимися новшествами как слабое, можно с хорошей точностью применить метод теории возмущений. Для этого систему (3)-(4) можно переписать в виде
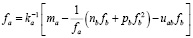, (5)
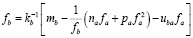. (6)
Систему (5)-(6) можно решать, взяв, например как начальное приближение
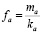, (7)
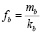. (8)
и подставляя эти значения в правую часть системы последовательными итерациями уточнить результат. В этом случае мы можем искать решение, при котором «выживают» и сосуществуют в стабильном состоянии оба новшества одновременно. Наряду с таким решением следует учитывать и ситуацию, когда одно из новшеств не выдерживает конкуренции и одно из выражений (7) или (8) следует заменить нулем. Найдя же решение, где оба новшества сосуществуют, и, подставив его в систему (1)-(2), можно изучить поведение малых отклонений – будут ли они затухающими, либо, напротив, покажут неустойчивость (метастабильность) такого решения.
Для уравнений (3)–(4), проведя описанные выше вычисления, получим
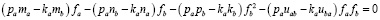, (9)
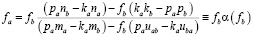. (10)
Аналогично (9), вычтя из (4) выражение (3), умноженное на kb/pb, получим
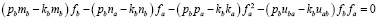. (11)
Подставив (10) в (11) получим
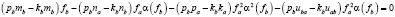. (12)
Решив теперь квадратное уравнение (12) относительно fb и выразив решение через коэффициенты, включающие a(fb), мы получим нелинейное уравнение одной переменной – вполне подходящее для решения его методом итераций. Действительно, в случае, когда коэффициенты перед нелинейными членами в (3)-(94) малы по сравнению с коэффициентами перед членами линейными, тогда a(fb) «слабо» зависит от fb и потому итерационное решение будет достаточно точным уже на первых шагах. Найденное решение может рассматриваться как возможное «стабильное» решение, только если найденные значения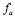 
и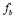 
будут больше нуля. Кроме того, такое решение должно быть «точкой притяжения», а не «точкой отталкивания». Заменив в (1)-(2) переменные 
, 
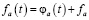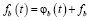и, рассматривая только линейные по j члены, получим систему уравнений вида
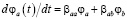, (13)
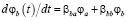(14)
с матрицей b, определяющей свойства решения (затухание к стабильной точке, либо «отталкивание»).
Для уравнений (3)-(4) следует также рассмотреть случаи, когда выживает только одно из двух новшеств, тогда, например, положив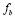 
= 0, мы получим
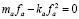. (15)
Уравнение же (15) имеет в свою очередь также два решения – уничтожение новшества (fb=0) или стабильное состояние насыщения (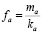
). Использование же для анализа найденного решения линеаризованной системы уравнений (13)-(14) может в этом случае быть не совсем корректным ввиду того, что даже при малых отклонениях величин возможен выход их за область определения (отрицательные значения).
На первом этапе анализа, используя уравнения (1)-(2) и не учитывая распределение плотностей в пространстве, интересно проанализировать случаи, когда наличие второго новшества начинает реально сказываться на развитии первого новшества и когда результат изменяется критическим образом. При таком анализе большое количество свободных параметров системы уравнений затрудняет формулировку любых полученных результатов в наглядной форме.
Знак коэффициентов uab определяет, является ли пара новшеств «дружественной» или «конкурирующей». В качестве примера дружественной пары можно рассматривать распространение автомобилей и распространение автозаправочных станций. Другой пример – продажа товаров в ассортименте позволяет покупателю делать выбор и снижает вероятность того, что покупатель уйдет без покупки. Поэтому, если в продуктовом магазине одновременно на прилавке есть говядина, свинина, баранина и птица, то сразу трудно сказать – будут ли эти товары «дружественными» или «конкурирующими». В целом – эти товары конкурируют, удовлетворяют «почти» одну и ту же потребность и существенное снижение цены на один вид мяса может снизить потребление мяса других видов. С другой стороны, лучшая обеспеченность товарами широкого ассортимента ведет к повышению уровня жизни и развитию потребительского спроса.
В случае, когда рассматривается распространение только одного новшества в изотропном пространстве, достаточно использовать три коэффициента – предел насыщения, характерное время перехода к насыщению и коэффициент диффузии. Тогда, перейдя к безразмерным величинам (концентрации, времени и расстоянию) уравнение может быть записано как
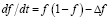, (16)
причем в уравнении (16) уже отсутствуют какие-либо свободные коэффициенты за исключением размерности пространства N, используемой в операторе лапласиана D. В случае, если мы рассматриваем распространение новшества от некоторой компактной области засева на значительные расстояния, процесс можно рассматривать как сферически симметричный. В этом случае расстояние R от центральной области начального засева является единственной существенной пространственной переменной. Тогда, отбросив в лапласиане члены, учитывающие пространственные вращения, получим
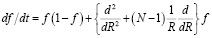. (17)
Уравнение (17) имеет один свободный параметр N, причем этот параметр «размерности» пространства может быть и не целым числом, если модель основывается на представлении о фракталах. Решение уравнения (17) представляет собой достигшее насыщения решение вплоть до радиуса R1, переходную зону вплоть до радиуса R2 и «незасеянное» пространство при больших расстояниях от области начального засева. Приняв условно для границ R1 и R2 концентрации, равными 90 % и 10 % соответственно, можно при различных параметрах N изучить, как ведут себя зависимости R1(t) и R2(t), а также «объемы»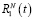 
и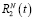 
при изменении эффективной размерности пространства.
Решение уравнения (17) представляет собой наиболее простой для анализа случай. Этот случай характеризуется наличием одной начальной области засева. В случае нескольких разных начальных областей засева фронты распространения от различных областей сталкиваются, выпуклый фронт при этом локально может стать вогнутым, что приводит к некоторому увеличению скорости распространения. Анализ решения в многомерном пространстве или для фрактальной модели при этом существенно усложняется.
Следующим шагом, после рассмотрения решения уравнения (16) может быть рассмотрение системы уравнений
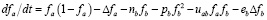; (18)
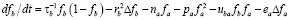, (19)
причем для второго новшества характерное время τb и характерный пространственный масштаб rb отличаются от аналогичных параметров, принятых за «единицу» для первого новшества. При этом величина «насыщения» для второго новшества также может быть нормирована на единицу. В том случае, когда характерное время установления для второго новшества много больше времени установления для первого, тогда в каждый момент времени развития второго новшества мы можем считать, что концентрация первого новшества не меняется. Тогда уравнение (18) просто выражает величину fa через fb, увеличивая, в итоге, нелинейность уравнения (19). Такое решение не представляет интереса, т.к. квадратичная нелинейность в исходных уравнениях была выбрана условно и ее вид не меняет принципиально картину развития процессов.
При наличии «быстрого» процесса, в каждый момент установившегося во времени, кажется, что просто меняются параметры среды распространения. И хотя параметры среды распространения на начальном этапе развития новшества и на этапе насыщения становятся разными, в области реального развития новшества, усредненные параметры могут быть выражены в рамках исходной модели с квадратичной нелинейностью.
Предположим теперь, что согласно уравнениям (18)-(19) первое новшество быстро развилось и достигло насыщения. Тогда для второго новшества уравнение принимает вид
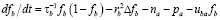, (20)
причем правая часть уравнения становится больше нуля при (оценочно) превышении порога
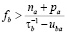. (21)
В этом случае второе новшество не сможет самопроизвольно развиться на занятом пространстве, если отсутствует начальная область с концентрацией, превышающей порог. На границе такой области и происходит реальная активная конкурентная борьба старого с новым. При рассмотрении такого процесса можно выделить две важных задачи – сферически-симметричное развитие и конкуренция новшеств на плоском фронте. В первом случае важна размерность пространства (если размер занятой сферы немного больше характерного размера ). Во втором случае – задача в пространстве становится одномерной и направление движения фронта конкуренции показывает, победит ли второе новшество либо оно не будет развито.
Развивая рассмотренный выше случай, использующий большое отличие характерных времен установления для двух разных новшеств, можно рассмотреть и случай с произвольным соотношением характерных времен и произвольным соотношением характерных размеров. Общий анализ такого случая сложен, так как любые результаты моделирования трудно представить в наглядной форме. Однако сразу же среди решений можно выделить случай, когда два разных новшества могут сосуществовать в некоторых процентных долях устойчиво, либо с колебательным процессом, либо развитие одного из новшеств полностью вытесняет другое. Последний случай приводит к появлению пространственного фронта борьбы, причем «толщина» такого фронта не может быть большой именно из-за «неуживчивости» двух новшеств между собой. В этом случае клеточная модель, в которой возникновение насыщения либо гибель на клетках зависит от ограниченного количества соседей клетки, будет достаточно реалистично отображать конкурентную борьбу. В случае же, когда новшества могут смешиваться и сосуществовать в течение длительного срока, пространственная структура и динамика границ играют меньшую роль именно из-за малой выраженности (размытости) этих границ. Следовательно, в общем случае изучения проблемы распространения новшеств можно выделить три разных по смыслу случая. В первом случае (например, система хищник-жертва) интересные решения, позволяющие делать выводы по возможностям управления процессом, возникают уже при рассмотрении только одной переменной – времени, без какого-либо учета пространственной структуры. Во втором крайнем случае – эффективная (фрактальная) размерность пространства важна, так как процессы разворачиваются на выраженных границах областей. В промежуточном случае существенного взаимопроникновения двух разных новшеств возможны сложные (например, колебательные) процессы, как во времени, так и в пространстве.
Ниже на рисунках иллюстрируется характерное поведение системы «хищник-жертва» для некоторых значений коэффициентов.
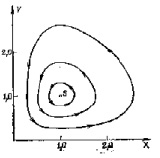
Рис. 1. Замкнутые фазовые траектории для модели хищник – жертва Видна аналогия с маятником без затухания. Задано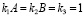 
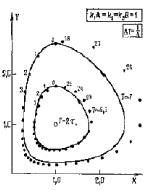
Рис. 2. Оценка траектории Используемые постоянные шаги по времени проясняют характер изменений фазовой скорости. Задано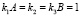 
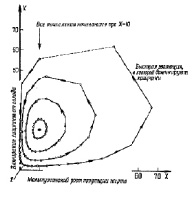
Рис. 3. Результаты численных расчетов, моделирующих эволюционную игру лиса – кролик: 1 – медленная независимая эволюция: хищники исчезают, жертвы размножаются
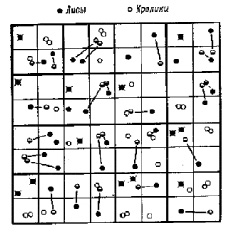
Рис. 4. Результаты типичного «хода» в эволюционной игре, показывающие мертвых лис, воспроизведенных кроликов и кроликов, которые попадаются на обед лисам. Здесь – перечеркнутый темный кружок это мертвые лисы, двойной пустой кружок это результат воспроизводства кроликов, наполовину закрашенный кружок – это превращение кролика в лису
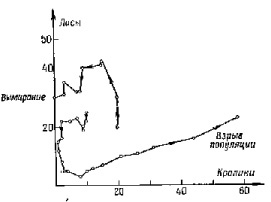
Рис. 5. Некоторые типичные результаты игры, демонстрирующие возможность вымирания кроликов или взрыв их популяции
Рис. 6. Некоторые типичные результаты игры, демонстрирующие возможность вымирания кроликов или взрыв их популяции
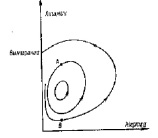
Рис. 7. Возможное неправильное управление экологией на основе стратегии, которая на первый взгляд кажется правдоподобной
Таким образом, предложена математическая модель распространения новшеств с использованием стохастической фрактальной модели и проведены иллюстративные расчеты для некоторых конкретных случаев.
Библиографическая ссылка
Лугин В.Г. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ НОВШЕСТВ С ИСПОЛЬЗОВАНИЕМ СТОХОСТИЧЕСКОЙ ФРАКТАЛЬНОЙ КЛЕТОЧНОЙ МОДЕЛИ // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 4. – С. 109-114;URL: https://applied-research.ru/ru/article/view?id=5082 (дата обращения: 23.11.2024).