В существующей на сегодняшний день теории принятия решений как в условиях риска, так и в условиях полной неопределенности [3, 6], используется матрица платежей, или равносильная ей, матрица рисков. В платежной матрице содержатся данные о возможных альтернативах, предполагаемых состояниях природы, а также количественные меры результатов, выражаемые в виде прибыли или убытка, при каждом сочетании альтернативы и состояния природы. В условиях риска в матрицу платежей добавляется еще строка с известными (из тех или иных соображений) объективными вероятностями состояний природы. Принятие наилучшего решения осуществляется на основании матрицы платежей. Причем в условиях риска – путем вычисления ожидаемых платежей с выбором наилучшего решения, соответствующего максимальному их значению, а в условиях полной неопределенности – на основании различных критериев (Вальда, Сэвиджа, Гурвица и пр.), которые, однако, противоречат друг другу, что затрудняет окончательный выбор.
Используемые в теории принятия решений модели – в условиях риска и полной неопределенности – являются неадекватными. Так, модель принятия решений в условиях риска требует знания объективных вероятностей наступления различных состояний природы. Между тем, применение объективных (классических, статистических) вероятностей к человеческой деятельности в любой сфере – экономике, социологии, менеджменте, психологии и пр. – неправомерно, поскольку последние не являются вероятностными объектами (подробнее см. [1, 4, 5, 7]). Обе модели – в условиях полной неопределенности и в условиях риска – исходят из допущения, что будущий результат принятого решения при каждом сочетании «решение – состояние природы» является единственным и строго определенным. Между тем, в результате принятого решения в будущем может реализоваться множество самых разнообразных исходов, носящих как благоприятный (шансы), так и неблагоприятный (риски) для субъекта характер [4], причем какие именно состояния природы и конкретные результаты актуализируются в будущем являются полностью неопределенными и непредсказуемыми. Поэтому при рассмотрении различных сочетаний «решение – возможное состояние природы» необходимо анализировать все возможные шансы (прибыли, удачи) и риски (ущербы, неудачи).
Вместе с тем, в существующей литературе по принятию решений в различных областях (экономике, менеджменте и пр.) рассматриваются исключительно риски. Вместе с тем, психология принятия решений свидетельствует об ином: человек предпринимая ту или иную деятельность руководствуется в первую очередь теми преимуществами и возможностями, которые сулит ему достижение поставленной цели и только в последнюю очередь рассматривает возможные неудачи и трудности на своем пути. В противном случае, то есть при ориентации только на неудачу, будет отсутствовать мотивация, необходимая для начала любой деятельности. Здесь мы солидарны с великим экономистом Дж. Кейнс, который полагал, что именно мотивация на успех, а не на будущие возможные неудачи, заставляет субъекта принимать решение и действовать, воплощая его в жизнь [2]. В силу сказанного, при принятии решения необходимо анализировать как шансы, то есть выгоды, так и риски, то есть препятствия и неудачи, но не одни лишь риски, как это сложилось в литературе («риск-менеджмент», «рискология» и пр.).
В данной статье рассматривается метод для принятия наилучшего решения в условиях полной неопределенности, который учитывает прогнозы и оценки наступления в будущем множества результатов (шансов и рисков), которыми может завершиться принятое решение. Метод использует модифицированную матрицу платежей (вместо обычной матрицы платежей), отражающую реализацию в будущем множества шансов и рисков при каждом сочетании «принятое решение – состояние природы». Наилучшее решение принимается на основе максимального значения комплексного критерия, отражающего баланс между всеми суммарными шансами и всеми суммарными рисками. Для визуального отображения соотношений между суммарными шансами и рисками вводится диаграмма шансов и рисков. Применение метода рассмотрено на конкретном примере.
Процедура принятия решения в условиях неопределенного будущего, с учетом прогнозировании и оценки множества шансов и рисков.
Процедуру, реализующую разработанный метод рассмотрим на модельном примере газетного киоска: продавец газет закупает газеты у поставщика накануне вечером по цене 1 у.д.е., а продает их на следующий день утром по цене 2 у.д.е. [3, 6]. Объем спроса на газеты априори не известен, поэтому продавец не знает сколько газет ему следует закупить, чтобы, с одной стороны, не упустить свою выгоду, если закупит мало газет, а с другой – не остаться с нераспроданными газетами, если закупит их слишком много.
Природой здесь является спрос на газеты на следующий день, состояниями природы (С) – объем неизвестного ожидаемого спроса (ОС), относительно которого продавец полагает, что завтра он может составить 1 экз. – состояние С1, 2 экз. – состояние С2 или 3 экз. – состояние С3. Содержанием решения (А) продавца является выбор объема закупаемых газет (ОЗ) накануне: 1 экз. (решение А1), 2 экз. (решение А2) или 3 экз. (решение А3). Значения платежей (прибыли или убытка) П, у.д.е. рассчитываются как П = 2 у.д.е. × min{ОС,ОЗ} – 1 у.д.е.×ОЗ. Предполагается, что вероятности наступления состояний природы по оценкам продавца газет составят соответственно 0,2 (для С1), 0,6 (для С2) и 0,2 (для С3).
Рассмотрим принятие решений с двух точек зрения: по существующей теории принятия решений и по предлагаемому методу.
Существующая теория принятия решений. В существующей теории принятия решений используются стандартная матрица платежей (табл. 1) и критерий принятия решения, представляющий собой ожидаемый платеж [3]. При этом делается неявное допущение, что при данном конкретном сочетании «решение – состояние природы» результатом будет один единственный исход (прибыль/убыток), наступающий с вероятностью 1 (табл. 1).
Таблица 1
Стандартная матрица платежей модели продавца газет
|
Альтернативы (А) |
Состояния природы – ожидаемый спрос на газеты, экз. |
Ожидаемые платежи |
||
|
С1 |
С2 |
С3 |
||
|
А1 |
1 |
1 |
1 |
1∙0,2 + 1∙0,6 + 1∙0,2 = 1 |
|
А2 |
0 |
2 |
2 |
0∙0,2 + 2∙0,6 + 2∙0,2 = 1,6 |
|
А3 |
– 1 |
1 |
3 |
(– 1)∙0,2 + 1∙0,6 + 3∙0,2 = 1 |
|
Вероятности состояний природы |
0,2 |
0,6 |
0,2 |
|
Наилучшим будет решение А2, соответствующее максимальному значению ожидаемого платежа (1,6 у.д.е)
Вместе с тем, допущение, при котором каждое сочетание «решение – состояние природы» завершается с вероятностью 1 одним единственным результатом (табл. 1) – прибылью или убытком – не может быть признано адекватным реальной практике, поскольку любое решение всегда приводит к множеству различных последствий, каждое из которых может актуализироваться в реальности с той или иной вероятностью.
Предлагаемый метод принятия решений. Рассмотрим процедуру принятия решений предлагаемым методом. В данном примере решение при каждом состоянии будущего спроса, может иметь различные последствия: (а) получение прибыли (шанс), (б) убытки из-за несоответствия предложения спросу (риск), (в) упущенная выгода, как альтернативная прибыль от инвестирования тех же средств в иной проект (риск), (г) утрата части клиентов, если продаваемые продавцом газеты будут в постоянном дефиците (риск), (д) рост объема продаж, если закупаемые продавцом газеты будут пользоваться спросом (шанс) и прочие. Примем для простоты, что множество шансов и рисков, которые могут актуализироваться в будущем имеют следующее содержание: (а) все закупленные газеты будут распроданы с наибольшим доходом (шанс ch1), (б) ни одна газета не будет продана и продавец понесет убытки (риск ri1), (в) будет продано газет меньше, чем ожидалось, так что продавец газет недополучит часть дохода (риск ri2).
Для реализации метода составляется модифицированная матрица платежей (табл. 2). Каждая ячейка матрицы содержит данные по шансам и рискам (ch1, ri1, ri2), которые могут актуализироваться при различных сочетаниях «решение Аi – состояние природы Сj», то есть (Аi, Сj).
Таблица 2
Модифицированная матрица платежей продавца газет
|
Решения (А) |
Шансы ch1 и риски ri1, ri2 |
Количественные меры (М), вероятности (Р) и величины (Ch1/Rk) шансов / рисков при состояниях природы |
Полная величина шанса / риска |
Полная вероятность шанса / риска |
||||||||
|
С1 |
С2 |
С3 |
||||||||||
|
M |
P |
Ch1/ Rk |
M |
P |
Ch1/ Rk |
M |
P |
Ch1/ Rk |
||||
|
А1 |
ch1 |
2 |
0,4 |
0,8 |
2 |
0,6 |
1,2 |
2 |
0,8 |
1,6 |
1,2 |
0,6 |
|
ri1 |
1 |
0,3 |
0,3 |
1 |
0,2 |
0,2 |
1 |
0,1 |
0,1 |
0,2 |
0,2 |
|
|
ri2 |
0 |
0,3 |
0 |
2 |
0,2 |
0,4 |
2 |
0,1 |
0,2 |
0,28 |
0,2 |
|
|
А2 |
ch1 |
2 |
0,1 |
0,2 |
4 |
0,5 |
2 |
4 |
0,7 |
2,8 |
1,8 |
0,46 |
|
ri1 |
1 |
0,4 |
0,4 |
1 |
0,3 |
0,3 |
1 |
0,2 |
0,2 |
0,3 |
0,3 |
|
|
ri2 |
0 |
0,5 |
0 |
2 |
0,2 |
0,4 |
4 |
0,1 |
0,4 |
0,32 |
0,24 |
|
|
А3 |
ch1 |
2 |
0,3 |
0,6 |
4 |
0,5 |
2 |
6 |
0,6 |
3, 6 |
2,04 |
0,48 |
|
ri1 |
1 |
0,5 |
0,5 |
1 |
0,3 |
0,3 |
1 |
0,3 |
0,3 |
0,34 |
0,34 |
|
|
ri2 |
0 |
0,2 |
0 |
2 |
0,2 |
0,4 |
4 |
0,1 |
0,4 |
0,32 |
0,18 |
|
|
Субъективные вероятности состояний природы |
0,2 |
0,6 |
0,2 |
|||||||||
В табл. 2 введены следующие обозначения и вычисляемые величины:
– субъективные вероятности актуализации (Р-столбцы в табл. 2) шансов и рисков 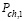 (Аi, Сj),
(Аi, Сj), 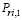 (Аi, Сj),
(Аi, Сj), 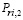 (Аi, Сj), назначенные продавцом/экспертом;
(Аi, Сj), назначенные продавцом/экспертом;
– количественные меры (М – столбцы в табл. 2) шансов и рисков, рассчитываемые по формулам: 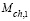 (Аi, Сj) = 2 у.д.е. × min{ОС,ОЗ},
(Аi, Сj) = 2 у.д.е. × min{ОС,ОЗ}, 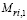 (Аi, Сj) = 1 у.д.е.×ОЗ,
(Аi, Сj) = 1 у.д.е.×ОЗ, 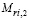 (Аi, Сj) = 2 у.д.е.×РС (РС – реальный спрос, оказавшийся меньшим ожидаемого; здесь принято, что РС = ОС – 1);
(Аi, Сj) = 2 у.д.е.×РС (РС – реальный спрос, оказавшийся меньшим ожидаемого; здесь принято, что РС = ОС – 1);
– величины шансов Ch(Аi, Сj) и рисков Rk(Аi, Сj), k = 1, 2 (Ch1/Rk – столбцы в табл. 2), равные произведениям количественных мер M(Аi, Сj) и вероятностей актуализации P(Аi, Сj);
– полные величины шансов Ch1(Аi) и рисков Rk(Аi), k = 1, 2 для каждого решения Аi, i = 1, 2, 3, равные усредненным по вероятностям всех состояний природы Сj (j = 1, 2, 3) величин шансов и рисков [4]:
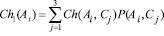 ,
,
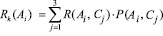 .
.
Например, полная величина шанса для решения А1 будет равна (табл. 2): Ch1(А1) = 0,8∙0,2 + 1,2∙0,6 + 1,6∙0,2 = 1,2;
– полные вероятности актуализации шансов Pch,1 (Аi) и рисков Pri,1(Аi), Pri,2 (Аi) [4], с которой полные величины шансов и рисков, соответствующие каждому решению Аi, i = 1, 2, 3, актуализируются в будущем. Определяются усреднением по вероятностям P1, P2, P3 состояний природы С1, С2, С3. Например, полная вероятность шанса для решения А1 составит (данные см. в табл. 2) Pch,1 (А1) = Pch,1 (А1,С1)∙P1 + +Pch,1 (А1,С2)∙P2 +Pch,1(А1, С3)∙P3 = 0,4∙0,2 + +0,6∙0,6 + 0,8∙0,2 = 0,6.
По вычисленным значениям полных величин шансов и рисков, а также полным вероятностям их актуализации (табл. 2), определяются значения суммарных шансов Ch(Аi) и суммарных рисков R(Аi) (табл. 3) для каждого решения Аi [4]:
Ch(Аi) = Ch1(Аi)∙ Pch,1 (Аi),
R(Аi) = R1(Аi)∙ Pri,1 (Аi) + R2(Аi)∙ Pri,2 (Аi).
Например, суммарный риск для решения А2 составит
R(А2) = 0,3∙0,3 + 0,32∙0,24 = 0,1668.
Таблица 3
Суммарные шансы Ch(Аi), суммарные риски R(Аi) и комплексный критерий R&Ch
|
Решения (А) |
Суммарный шанс |
Суммарный риск |
Комплексный показатель шансов и рисков |
|
А1 |
0,72 |
0,096 |
0,624 |
|
А2 |
0,828 |
0,1668 |
0,6612 |
|
А3 |
0,9792 |
0,1732 |
0,806 |
Принятие окончательного решения основывается на максимизации комплексного критерия [4]
R&Ch(Аi) = βCh Ch(Аi) – βR R(Аi),
по всем комплексным критериям, рассчитанным для каждой альтернативы Аi.
Комплексный критерий R&Ch(Аi) характеризует соотношение баланса между благоприятными (шансами) и неблагоприятными (рисками) для субъекта результатами принятого решения Аi. Наилучшее решение будет соответствовать максимальному значению критерия R&Ch среди всех остальных решений. Коэффициенты βCh и βR отражают относительную важность шансов и рисков с точки зрения склонности субъекта к риску: при его склонности к риску βCh < βR, при осторожном отношении βCh > βR, при нейтральном отношении βCh = βR. В данном примере примем, что субъект одинаково относится как к шансам, так и рискам, то есть βCh = βR = 1.
Значения комплексного показателя R&Ch(Аi), вычисленные для каждого решения (табл. 3) позволяют заключить, что наилучшим будет решение А3, соответствующее максимальному значению критерия R&Ch(А3) = 0,806. Таким образом, согласно предлагаемому методу рекомендуется принять решение А3, в отличие от решения А2, рекомендуемого обычной существующей теорией принятия решений со стандартной матрицей платежей (табл. 1). Принятие решения А3 является более адекватным реальной действительности, поскольку принимает во внимание множественность возможных исходов решений. Для наглядного отображения суммарных шансов и рисков служит [4] диаграмма шансов и рисков (рисунок).
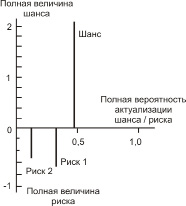
Диаграмма шансов и рисков для решения А3
Заключение
Разработанный в статье метод позволяет принимать наилучшие решения в условиях полной неопределенности, с учетом прогнозирования и оценки множества возможных результатов и последствий (шансов и рисков) принятых решений. Структуру данных для принятия решений отражает введенная модифицированная матрица платежей, значительно отличающаяся от обычной, полнотой представления множества возможных будущих результатов принятых решений. Наилучшее решение принимается на основании максимизации комплексного критерия, характеризующего соотношение баланса между суммарными величинами шансов и рисков, а также – диаграммы, в визуальном виде представляющей баланс между ними. Алгоритм разработанного метода продемонстрирован на конкретном модельном примере.
Библиографическая ссылка
Мадера А.Г. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ ПРИ АКТУАЛИЗАЦИИ В БУДУЩЕМ МНОЖЕСТВА ВОЗМОЖНЫХ ШАНСОВ И РИСКОВ // Международный журнал прикладных и фундаментальных исследований. 2014. № 4. С. 136-140;URL: https://applied-research.ru/ru/article/view?id=5087 (дата обращения: 03.03.2026).


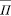 , у.д.е.
, у.д.е.