К современным тенденциям стратегического управления предприятием [1, 2] относится создание структуры, занимающейся, в частности, разработкой программного обеспечения для поддержки принятия решений руководителем предприятия. Рассматривается одна из задач, решение которой обеспечивает указанную выше поддержку принятия решений руководителем по повышению эффективности деятельности предприятия в смысле рационального расходования его ресурсов при повышении критериев его функционирования.
Постановка задачи[1]. На предприятии имеется N расходных подразделений (структур), требующих для своего функционирования денежных вложений. Каждое подразделение ежегодно вносит вклад в обобщённый критерий функционирования предприятия при определённых денежных вложениях в неё. При очередном вложении денежных средств каждая структура планирует в конце отчетного интервала времени увеличить обобщённый критерий функционирования предприятия на заданный показатель с указанием риска невыполнения ей этого показателя. Руководитель предприятия имеет в распоряжении определённую сумму денег для вложения в указанные расходные структуры в начале отчётного интервала времени и по своему усмотрению определяет доли каждой структуре из общей выделенной суммы на все подразделения. Задача заключается в определении денежных сумм, планируемых для выделения каждому подразделению при условии достижения максимума величины обобщённого критерия функционирования предприятия.
Математическое описание. Введем функцию вида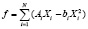 
, представляющую собой планируемый вклад в величину обобщённого критерия функционирования всеми подразделениями. Первое слагаемое под знаком суммы – планируемый вклад в величину f структуры номер i, второе слагаемое – риск невыполнения этого планируемого вклада, Xi – денежная сумма, планируемая для выделения структуре номер i, подлежащая определению в рассматриваемой задаче, Ai – заданный коэффициент, связывающий величину вклада в критерий подразделением номер i c суммой денежного вклада в него, bi – заданный коэффициент, связывающий величину риска невыполнения планируемого вклада в величину критерия подразделения номер i c суммой денежного вклада в него.
Условие руководителя предприятия в выделении средств расходным подразделениям предприятия представим зависимостью вида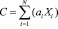 
, где С – планируемая к выделению расходным структурам сумма, ai – весовой коэффициент, назначенный руководителем предприятия для структуры номер i. В частности, эти коэффициенты могут быть равными единицам.
Согласно постановке задачи, необходимо максимизировать функцию f при условии C.
Сформулированная задача – это задача на условный экстремум функции нескольких переменных, которые по смыслу задачи должны быть положительными действительными числами.
В соответствии с методом решения таких задач, использовав функцию f и условие C, составляем функцию Лагранжа
,
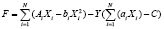где Y – дополнительная переменная.
Необходимые условия экстремума функции Лагранжа F или условного экстремума функции f есть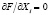 
, следовательно,
, 
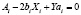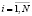; (1)
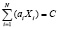. (2)
Для определения достаточных условий максимума функции Лагранжа F можно воспользоваться критерием Сильвестра, для чего следует найти значения вторых частных производных этой функции в точках экстремума, составить из них определитель, а затем составить известные неравенства путём выделения из этого определителя «диагональных определителей» и вычислить их. В результате реализации этой процедуры будут наложены ограничения на параметры функции F, при которых достигается её максимум. В данной задаче удобнее использовать второй способ определения достаточных условий – это определение знака второго дифференциала функции F. В данном случае второй дифференциал функции Лагранжа F имеет вид
.
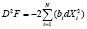Так как по смыслу задачи коэффициенты bi положительны, то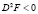 
, а значит, функция F в точке экстремума имеет максимум.
Для определения экстремальных значений Xi необходимо решить систему (1), (2), состоящую из (N+1)-го уравнения относительно (N+1) неизвестных Xi, Y. Решив систему (1) относительно Xi, получим:
, 
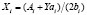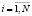. (3)
Подставив найденные решения Xi в уравнение (2), получим уравнение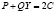 
и решим его относительно Y:
.
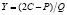Здесь введены обозначения:
, 
.
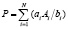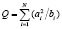Подстановка Y в (3) даёт решения для значений Xi, максимизирующих функцию f. Вклад каждого подразделения в приращение критерия функционирования предприятия в процентах определяется формулами
, 
,
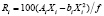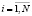где f – значение функции при указанных выше максимизирующих её значениях аргументов.
[1] Постановка задачи согласована с Механовым Д.С.
Библиографическая ссылка
Слепова С.В., Шахина М.А., Щипицын А.Г. МАКСИМИЗАЦИЯ КРИТЕРИЕВ ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ ПРЕДПРИЯТИЯ ОТ ВЛОЖЕНИЯ СРЕДСТВ В ЕГО РАСХОДНЫЕ ПОДРАЗДЕЛЕНИЯ // Международный журнал прикладных и фундаментальных исследований. 2014. № 4. С. 182-183;URL: https://applied-research.ru/ru/article/view?id=5100 (дата обращения: 09.05.2025).