Проведем небольшой ретроспективный анализ вопроса о принятии и совершенствовании стандартов школьного образования. Обновление образовательных стандартов проходило в России дважды – в 1998 и в 2004 годах. Но особых изменений в школьную жизнь эти обновления не внесли, практически все осталось по-прежнему. В декабре 2004 г. было принято решение Правительства РФ о разработке стандартов второго поколения. В чем была основная необходимость разработки новых стандартов?
Стандарты первого поколения создавались, во-первых, в условиях развала СССР, исчезновения сверхдержавы, резкой смены идеологических и политических векторов нашей жизни. Эти стандарты прошли под лозунгом деидеологизации и гуманизации образования. Вторая отличительная особенность тех стандартов заключалась в том, что они, с одной стороны, сконцентрировались на отборе нового содержания образования, а с другой – формировались в условиях невнятных идеологических и политических установок.
Отличительной особенностью новых федеральных государственных образовательных стандартов (ФГОС), принятых в 2010 г., является их личностная ориентация – отказ от предметного центризма и переход к личностной центрации образования. Цель образования рассматривается как подготовка человека к будущей деятельности в обществе, а содержание образования – как освоение общих методов и форм человеческой деятельности.
Новые ФГОС отвечают идеям компетентностного подхода, определяющего целевую ориентацию учебного процесса на формирование определенных компетенций, отражающие готовность человека действовать в конкретных ситуациях.
Для достижения результатов обучения, которые отмечены в новых ФГОС, нужны соответствующие педагогические технологии. Оставаясь лишь в рамках классно-урочной системы вряд ли можно достичь этих результатов.
Начальные школы России с 1 сентября 2011 года стали работать по новых Федеральным государственным образовательным стандартам начального обшего образрвания.
24 декабря 2013 года распоряжением Правительства Российской Федерации за номером 2506-р принята Концепция развития математического образования в Российской Федерации. В ней отражены цели создания Концепции, рассмотрены современное состояние, задачи, подходы к организации математического образования.
В документе указаны три уровня требований к результатам математической подготовки:
- первый уровень – для успешной жизни в современном обществе;
- второй уровень – для прикладного использования математики в дальнейшей учебе и профессиональной деятельности;
- третий уровень – для подготовки к продолжению образования и творческой работе в математике и смежных с ней научных областях.
Конечно, в документе есть неясности и даже туманности. Например, что значат слова: «Достижение какого-либо из уровней подготовки не должно препятствовать индивидуализации обучения и закрывать возможности продолжения образования на более высоком уровне или изменения профиля»?
Школа должна предоставить каждому учащемуся, независимо от места и условий проживания, возможность достижения любого из названных выше уровней математического образования в соответствии с его индивидуальными потребностями и способностями.
Обеспечение этого требования напрямую зависит от учительских кадров, подготовка которых должна отвечать современным требованиям.
Сейчас российская единообразная система получения высшего профессионального образования, в том числе и педагогического, сменяется новой многоуровневой системой, существенно отличающейся от моноуровневой как по содержанию, так и по структуре организации.
По новой многоуровневой формуле обучения на получение общего высшего образования отводится четыре года (программа бакалавриата), а на овладение специализированными знаниями и профессиональными навыками два года (программа магистратуры).
К сожалению, в стандартах и других нормативных документах до сих пор четко не разделены сферы деятельности бакалавра и магистра образования. Заметим, что уже в вузе следует развести приоритеты при подготовке бакалавров и магистров. Бакалавриат должен предоставлять основу знаний необходимых для работы учителя математики. Магистратура же завершает подготовку квалифицированного учителя математики для профильной школы.
Одним из основных критических замечаний к современным образовательным стандартам является явное несоответствие количества часов, отводимых на изучение дисциплины, в данном случае математики, и объема материала, необходимого для обучения будущего учителя математики.
Новые образовательные стандарты требуют активизации самостоятельной работы студентов, что влечет за собой другую методику организации лекционных и практический занятий. В этой связи лекции все больше приобретают обзорный характер, а практические занятия – черты семинарских.
В 2002 году академик В.И. Арнольд на парламентских слушаньях в Государственной думе РФ произнес знаменитую речь о состоянии математического образования, которая получила большой резонанс и, возможно, отстрочила поспешное принятие новых стандартов образования в средней и высшей школе. В этом выступлении академик свидетельствовал: «По статистике Американского математического общества в сегодняшних Штатах разделить число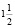 
на 
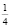может, в зависимости от штата, от одного до двух процентов школьных учителей математики. Из «стандартов» простые дроби давно у них исчезли, поскольку компьютеры считают только десятичные. Большинство американских университетских студентов складывают числители с числителями и знаменатели со знаменателями складываемых дробей: 
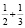есть, по их мнению, 
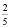. Обучать после такого «образования» думать, доказывать, правильно рассуждать никого уже невозможно, население превращается в толпу, легко поддающеюся манипулированию со стороны ловких политиков без всякого понимания причин и следствий их действий» [15].
С тех пор прошло одиннадцать лет, В.И. Арнольд ушел в мир иной, но его слова звучат как набат всем педагогам, радеющим за отечественное математическое образование.
Подобную картину, но уже в школе, описывает М.А. Чошанов: «Участникам эксперимента – ученикам начальных классов США и России – предлагалась задача: «Пастух с пятью собаками охраняет стадо из 125 овец. Сколько лет пастуху?». Результаты: 70 % российских школьников сразу же заподозрили, что в той задаче «то-то не то», «чего-то не хватает». В результате они сделали вывод, что в задаче не хватает информации, и сформулировали ответ: «Задача не имеет решения». В то время как 75 % (!) американских школьников пытались найти численное решение данной задачи. Вот как они рассуждали: «125+5=130 (… слишком старый пастух), 125-5=120 (… пастух все равно очень старый),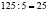 
(… теперь о’кей! ответ: пастуху 25 лет)». Оказывается, американских школьников попросту не учат правильно решать задачи» [18 , с. 5].
О.А. Саввина, размышляя о стандартах последнего поколения для педагогического образования (ФГОС по направлению подготовки 050100.62 «Педагогическое образование»), задается вопросом: «А не получит ли «передовой» американский опыт распространение в России?» [16, с. 34].
Многие ученые и практики отмечают резкое снижение качества математического образования в России.
Ректор МГУ академик В.А. Садовничий заявил на сентябрьском 2009 г. заседании Российского съезда ректоров, что примерно 60% первокурсников двух факультетов «провалили» контрольную по математике единого госэкзамена (факультеты математики и вычислительной математики). И это в самом элитном российском вузе! А что в других вузах?
Преподаватель Ростовского государственного экономического университета В.А. Деминский провел в начале 2009/10 учебного года самостоятельную работу среди студентов. Вот как выглядело типовое задание:
Решите систему уравнений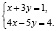 
Решите уравнение 2х2 +3х+1=0.
Выполните действие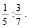 
С первым заданием из 190 человек справились только 39 % участников исследования, правильно выполнить все три задания смогли лишь 50 студентов (27 % от общего числа первокурсников). 29 человек (16 %) не смогли решить ни одного задания.
И.П. Костенко в статье «Кризис отечественного математического образования» [14] проследил генезис качества математического образования в России и назвал этапы:
- падение качества знаний (1920-е годы);
- рост качества знаний (1930-е годы);
- дальнейший рост качества знаний (1940-е годы);
- продолжение роста качества знаний (1950-1956 годы);
- резкое падение качества знаний (1956-1960 годы);
- замедленное падение качества знаний (1960-е годы);
- обвальное падение качества знаний (1970-е годы);
- продолжение падения качества знаний (1980-е годы);
- на дне (1990-2012 годы).
В.А. Болотов, будучи в 2009 году заместителем министра образования РФ, признавал, что 70 % школьников «не осваивают математику и физику».
Заслуживает внимания суждение учителя математики Д.Д. Гущина о том, что наше «лучшее физико-математическое образование» уже настолько не лучшее, что даже и не образование.
Если оставаться в рамках подготовки бакалавров по действующим учебным планам, то нужно срочно искать эффективные пути и средства повышения качества математической подготовки студентов.
Важным средством является самостоятельная работа студентов, которая позволяет наряду с предметными знаниями, овладевать теми видами деятельности, которые характерны для будущей профессиональной деятельности.
Анализ ФГОС высшего профессионального образования по направлению подготовки 050100 «Педагогическое образование» (квалификация (степень) «бакалавр») [17] показывает, что в них отсутствует предметная составляющая. В нем нет ни слова о том, что учитель-предметник должен знать свой предмет хотя бы в объеме школьного курса.
Новые стандарты написаны в контексте компетентностной парадигмы образования, противопоставившей их традиционной знаниевой парадигме. Тем самым из педагогического лексикона вычеркнуты устоявшиеся понятия: «знания», «умения» и «навыки». Но тогда как перевести на «компетентностный язык» совершенно ясные и понятные требования к математическому образованию, например: знать способы решения тригонометрических уравнений; уметь складывать обыкновенные дроби; уметь решать квадратные уравнения и т.д.
Ясно одно: предметная область должна занять в подготовке учителя, в том числе и учителя математики, свое надлежащее место.
В новых учебных планах подготовки бакалавров направления «Педагогическое образование», профиль «Математическое образование» резко сокращено число часов на математические дисциплины. Подтвердим сказанное фактами.
В учебном плане подготовки специалиста – учителя математики (срок обучения 4 года) в 1963 году на математическом факультете Омского государственного педагогического института им. А.М. Горького на изучение математического анализа отводилось 1000 часов и 192 часа на изучение дополнительных глав математического анализа, а в 2012 году в учебном плане бакалавриата по направлению «Педагогическое образование», профиль «Математическое образование» (срок обучения 4 года) отводится на изучение математического анализа 540 часов (это трудоемкость, из них 234 часа аудиторных), на дополнительные главы математического анализа отводится 108 часов (это трудоемкость, из них 26 часов аудиторных). На курс «Элементарная математика» в 1963 году на математическом факультете отводилось 640 аудиторных часов, а в 2012 году на этот же курс отводится лишь 360 часов (это трудоемкость, из них 162 часа аудиторных). Подобное обстоятельство имеет повсеместный характер.
Резкое сокращение числа часов в бакалавриате на математические дисциплины, как показывает практика, приводит к тому, что у студентов не формируются ни пресловутые предметные знания, умения и навыки, ни провозглашенные современными стандартами компетенции.
Надо заметить, что в стандартах общего образования также акцент сделан на «обеспечение преимущественно общеобразовательной и общекультурной подготовки». Отсюда и порядок расположения требований к результатам освоения основной образовательной программы: личностные, метапредметные и лишь на последнем месте предметные результаты.
С.Н. Бычков замечает: «заострение внимания на метапредметных и личностных результатах, выдвижение их на первый план излишне: математика сама своим собственным содержанием позволяет достигать всего сразу, следуя собственной двухтысячелетней традиции» [1, с. 58].
Библиографическая ссылка
Далингер В.А. НОВЫЕ ОБРАЗОВАТЕЛЬНЫЕ СТАНДАРТЫ И РОССИЙСКОЕ МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 4. – С. 207-210;URL: https://applied-research.ru/ru/article/view?id=5118 (дата обращения: 19.04.2024).