Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Наврузов К.Н. 1

---

1 Ургенчский государственный университет им. Ал-Хорезми

В статье приведены состав крови и её реологические модели. Анализированы литературные исследования по реологии крови в современном уровне. Обобщены существующие модели с точки зрения упруговязкопластической жидкости. При этом определены упругий, вязкий и пластический коэффициенты для крови.

Статья в формате PDF

1028 KB

реологическая модель крови

уравнение Кэссона

упругий коэффициент

вязкий коэффициент

пластический коэффициент

1. Файзуллаев Д.Ф., Наврузов К.Н. Обобщенная аппроксимационная модель неньютоновских жилкостей // Изв. А.Н. Узбекистана. Сер. тех. наук. 1985, №3 С. 54-58.

2. Наврузов К.Н., Хакбердиев Ж.Б. Динамика неньютоновских жидкостей. – Ташкент: Фан, 2000. – 246 с.

3. Наврузов К.Н. Биомеханика крупных кровеносных сосудов. – Ташкент: Fan va texnologiya, 2011, 144 с.

В больших кровеносных сосудах и в желудочках сердца при движении крови, скорость сдвига намного больше чем единицы. В связи с этим, в этих участках движение крови можно считать гомогенной средой, с осредненными параметрами: осредненная плотность, осредненное давление, осредненная скорость и др. В этом случае вязкость крови зависит от концентрации эритроцита или гематокрита H. Поэтому, вместо вязкости крови, используется кажущуюся вязкость, являющейся функцией от эритроцита. Во многих существующих работах, посвященные для составления реологические уравнения крови с осредненными параметрами, кроме констатации экспериментальных данных содержатся попытки сопоставления их с теми или иными известными в реологии соотношениями. В данной статьи предлагаемая модель крови, по существу не отличается от однофазной смеси. Однако здесь учитывается ее неньютоновские свойства в виде вязкопластичной, вязкоупругой и вязкоупругопластиной смеси а также все параметры входящие в уравнениях смеси, определяется со средними параметрами движения (средняя плотность, средняя скорость, кажущуюся коэффициенты вязкости смеси (крови)).

Судя по многим публикациям, и обработка экспериментальных данных в координатах 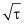, , 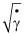что реологические свойства крови (только для стационарных течений) удовлетворительно описываются уравнением Кэссона, которая для чистого сдвига даёт соотношение 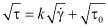[1].

, (1)

где t – напряжение, τ0 – предельное напряжение, 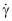– скорость сдвига, k – кэссоновскbq коэффициент вязкости. Из этой формулы видно, что модель Кэссона описывает нелинейно-вязкие свойства крови. Постоянные k и τ₀ могут быть функциями температуры и состава крови. В работе [2] обобщены кэссоновской и другие существующие вязкопластические модели в одной обобщённой модель с помощью разложения функции в ряды Тейлора

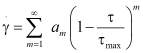, (2)

где am – коэффициенты ряда, определяемые из конкретных моделей с помощью формулы

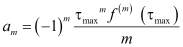. (3)

Кроме того, если экспериментально определена взаимосвязь между напряжением и скоростью сдвига в виде графика или таблицы, то это можно аппроксимировать с достаточной точностью методом наименьших квадратов или другими методами математической статистики. Тем самим определяется значение коэффициента a_m. Такой подход даёт возможность с одной стороны, обобщить существующие частные модели, с другой ликвидировать математические трудности при решении конкретно поставленных задач. Вязкопластичные модели крови существенно ограничены с точки зрения нестационарности [1], так как в этих моделях не учитывается временный эффект. Кроме того, отличающая от нуля разность первых нормальных напряжений в вискозиметрических течениях не может быть объяснена на основе предположения, что тензор напряжений однозначно определяется тензором деформации. Поэтому они могут быть использованы лишь в ламинарном стационарном течении. Так же они могут быть использованы в качестве первого приближения для колебательного потока при малой амплитуде. Отсюда втекает, что при использовании этих моделей в задачах, не касающихся вискозометрических течений таких как, течения крови по сосудам, надо быть осторожным, иначе в противном случае могут быть существенные пробелы при расчетах нестационарных переходных процессов. Поэтому здесь составление реологических уравнений крови, ее упругие свойства приобретает существенное значение. Наиболее распространенной моделью упруговязкой жидкости является обобщенная максвелловская модель. Она основана на одномерных механических моделях, составленных из «пружин» (упругость) и «поршней» (вязкость) [1-3].

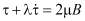, (4)

где 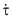– временная производная от тензора напряжений, λ – релаксационный коэффициент, μ – эффективный динамический коэффициент вязкости крови, τ – тензор напряжений. Добавление члена 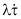содержащего временную производную от t, позволяет, представит с помощью данного уравнения явление релаксации напряжения, характерное для жидкости (крови) с памятью. Максвелловская модель жидкости может применяться для течения крови в крупных кровеносных сосудах, когда скорость сдвига 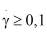. При мелких же сосудах, у движения крови обязательно появляется пластические свойства. Исходя из этих соображений, вместо релаксационной формулы Максвелла предложим реологическое уравнение, учитывающие пластические свойства крови в одноосном случае

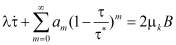. (5)

Здесь для модели Кэссона am имеет вид

,

.

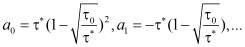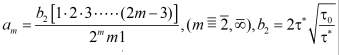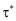– максимальное напряжение, при течении крови по кровеносным сосудам преобладает максимальное значение при 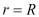, т.е., на стенки сосудах; τ₀ – предельная напряжения крови. τ₀ изменяется в промежутке 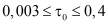(дин/см2) µk – кажущая вязкость крови определяется по формуле

,

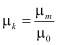где µ_m – относительная вязкость определяется из [3]. µ₀ – вязкость плазмы, 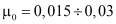пз Е – упругий коэффициент крови. Приблизительно, он равен 340 н/м2 l – релаксационный коэффициент. Определяется по формуле

.

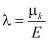Для крови, трёхэлементного упруговязкопластичного случая предложим новая модель, когда элементы состоят из двух вязких и одного упругого элемента. Формула, которая связывает напряжение и скорости деформации

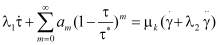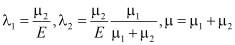, (6)

где λ₁, λ₂ – релаксационные коэффициенты, µ_k – кажущийся коэффициент вязкости крови при стационарном течении. Величины λ₁, λ₂, имеющие размерность времени, носят название времени релаксации, для напряжений и скоростей деформаций. Когда 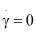(течение остановлено), напряжения, существовавшие в момент остановки, будут затухать (релаксировать) по закону 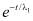, а при снятии напряжений, течение будет затухать по 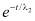. При исследовании жидкостей, проявляющих временные эффекты, прямое восстановление реологического соотношения усложнено, и потому чаще используют процедуру простого подбора коэффициентов в гипотонических моделях. В настоящее время на вискозиметрах, наиболее распространены два типа динамических экспериментов: измерения при периодическом (синусоидальном) изменении задаваемой прибором характеристики во времени, измерения релаксации напряжений или релаксации течения в переходных режимах, от одного стационарного течения к другому. Ниже рассмотрим первый тип измерения подбора коэффициентов.

Пусть колебательное течение происходит между пластинами, одна из которых неподвижна, а вторая совершает колебания по закону 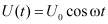, сопряжено с преодолением действующей на нее силы 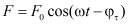пропорциональной напряжению сдвига на стенке. Для простоты положим, что частота 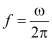не очень велика, так что ускорения в жидкости малы (точнее, силы инерции малы в сравнении с силами вязкости). Тогда течение будет квазистационарным во все моменты времени. Профиль скоростей линии, но его наклон, т.е скорость сдвига, периодически изменяется в фазе со скоростью границы:

.

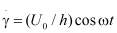Измерения амплитуды напряжений 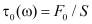и угла сдвига фаз 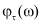при различных частотах позволяют вычислить динамическую вязкость h′ и коэффициент h″, являющейся мерой упругости:

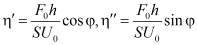. (7)

Комплексное число 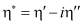называют комплексной вязкостью; его удобно использовать при теоретическом решении задач о вискозиметрических течениях. В этом случае ньютоновской жидкости соответствуют 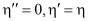. Для жидкости, описываемой реологическим уравнением в работе автора [3] параметры η′, η″ связаны с истинными реологическими коэффициентами η, λ₁, λ₂ формулами:

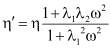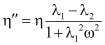; . (8)

Зная η из опытов со стационарными течением, по η′ и η″ можно восстановить значения λ₁ и λ₂. Если вычисленные так λ₁, λ2 оказываются одними и теми же для всех частот, то это подтверждает пригодность выше предложенного уравнения. Если же результаты вычислений зависят от частоты, то, следовательно, найдены только кажущиеся коэффициенты релаксации, а истинное реологическое уравнение могут, отличаться от выше найденного.

Библиографическая ссылка