Как известно, деформативные свойства грунтов меняются вместе с координатами точки, и допущение об их однородности представляет собой идеализацию реальных состояний. Конечно, при условии неоднородности, математическая задача несравненно сложна и, поэтому в таких случаях нередко прибегают к различным родам упрощения модели, приемлемым с той или иной точки зрения. При этом в одной группе задач параметры, характеризующие свойства материала, кусочно постоянны. Это означает, что исследуемое тело состоит из нескольких однородных тел. В другой группе задач они представляют собой непрерывные функции координат точки. Причем грунт, модуль деформации которого непрерывно увеличивается с глубиной, называется непрерывно неоднородным. В связи с этим в данной работе рассмотрим процесс уплотнения непрерывно неоднородных упругоползучих грунтов, состояние которых описывается выражением [1]
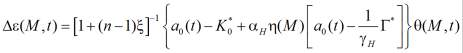, (1)
где
; 
; 
; 
;
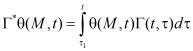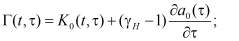
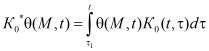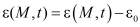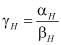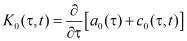– ядро ползучести, соответствующее однородной среде; 
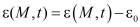; ε0 – начальный коэффициент пористости; x – коэффициент бокового давления; e(t) – коэффициент пористости для исследуемого момента времени t; 
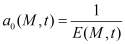– коэффициент мгновенного уплотнения; 
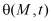– сумма главных напряжений; n – размерность рассматриваемой задачи.
Выражение (1) дает возможность оценить влияние неоднородности на общее состояние уплотнения упругоползучего грунта и является определяющей зависимостью между коэффициентом пористости и суммой главных напряжений, т.е. оно является основным уравнением, описывающим состояния непрерывно-неоднородных упруго-ползучих грунтов.
Процесс уплотнения трехфазной земляной среды без учета вязких свойств скелета и переменности коэффициента фильтрации согласно [7] описывается следующим образом
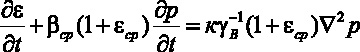, (2)
где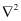 
– оператор Лапласа; 
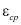– средний коэффициент пористости; 
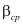и к – коэффициент объемного сжатия и фильтрации; р – давление в поровой жидкости, 
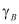– объемный вес воды.
Вместо e(t) в (2) подставив (1), соотношение (2) приводим к следующему виду:
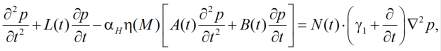(3)
где
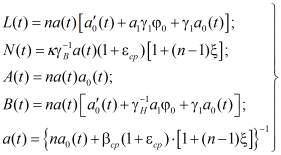. (4)
Для решения уравнения (3), помимо граничных условий имеем два начальных условия [1]:
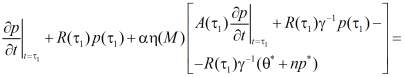
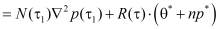; (5)
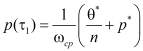. (6)
где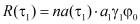 
; 
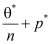– начальное распределение порового давления для двухфазной среды исследуемой задачи.
Таким образом, процесс уплотнения упругоползучих неоднородных грунтов математически будет описан дифференциальным уравнением вида (3) при начальных условиях (5), (6), т.е. вся задача сводится к определению решений уравнений (3) при соответствующих краевых условиях.
Для решения (3) при (4) – (6) обычно применяется метод возмущений, успешно используемый в теории упругости неоднородных тел [3]. Согласно этому методу вводится некоторый малый параметр g:
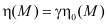. (7)
Здесь η0(М) – неоднородная функция, зависящая от координат.
Затем решение уравнения (3) ищется в виде:
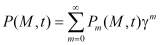. (8)
Выражения (7) и (8) подставим в (3), затем приравниваем коэффициенты при одинаковых степенях g. При этом получим
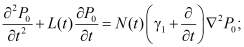(9)
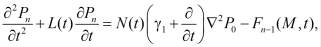(10)
где
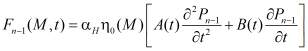. (11)
Начальными условиями для этих дифференциальных уравнений будут:
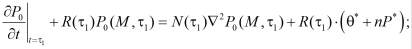
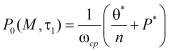; (12)
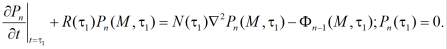(13)
Функция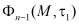 
, входящая в (13) имеет вид:
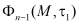
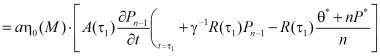(14)
Итак, для решения задач механики уплотнения упругоползучих неоднородных грунтов требуется найти непрерывные функции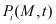 
, удовлетворяющие в области 
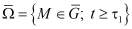системе линейных дифференциальных уравнений (9), (10) с начальными (12), (13) при (11), (14) и граничными условиями общего вида
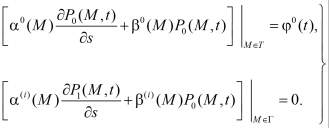. (15)
Здесь G – конечная область, ограниченная замкнутой кусочно-гладкой поверхностью Г; s – внешняя нормаль к Г.
.
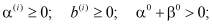
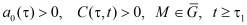В целом исследуемая задача относится к неоднородным задачам теории консолидации упругоползучих грунтов. Решение этой задачи, безусловно, предоставляет большие трудности. Однако знание собственных функций соответствующей однородной задаче позволяет решать и неоднородные.
Рассмотрим одномерную задачу теории консолидации многофазных неоднородных грунтов, обладающих свойством ползучести. Для этой задачи требуется определить давление в поровой жидкости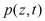 
, напряжение в скелете грунта 
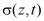и осадок уплотняемого слоя конечной мощности h.
Для данного случая вместо функци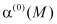и 
и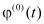 
, входящие в выражение при z =h имеем 
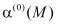=0,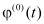 
=0, а при z = 0 имеем 
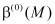=0 и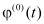 
=0. Следовательно, 
=
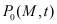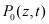=0, а собственная функция представляется в виде:
.
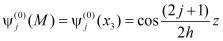Тогда выражение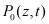 
запишется следующим образом:
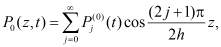(16)
где функция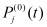 
, для данного случая имеет вид:
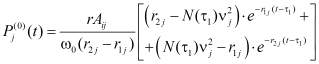. (17)
Определив и другие функции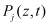 
распределение порового давления в неоднородном упруго-ползучем грунте можно представить в виде:
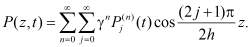(18)
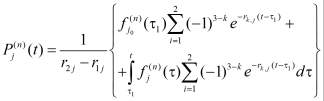
При этом напряжение в скелете грунта вычисляется по формуле
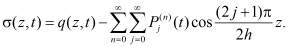
Для определения перемещения границ уплотняемого слоя воспользуемся известной формулой определения осадка:
.
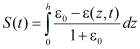Теперь рассмотрим решение краевой задачи (3)-(6) применительно к уплотнению слоя трехфазного упругоползучего грунта с водоупором на глубине h, ограниченном с боков водонепроницаемыми стенками, и находящимся под действием равномерно распределенной нагрузки q, приложенной на участке (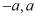
) поверхности массива.
Расчетная формула, которая дает возможность вычислить давление в поровой жидкости, т.е.
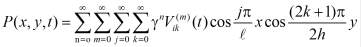. (19)
Величины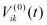 
, 
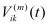в выражении (19) находятся из:
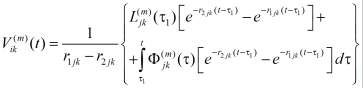, (20)
,
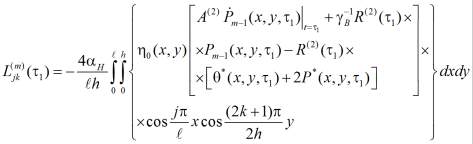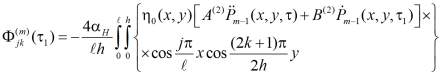
(21)
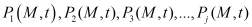– последующие решения задачи. Например, 
имеет вид:
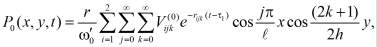(22)
где
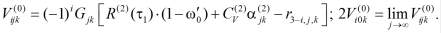(23)
Величина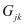 
, входящая в выражение (10) вычисляется по формуле
.
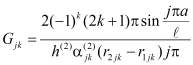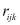– корни квадратного алгебраического уравнения;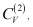 
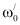Причем коэффициенты А(2), В(2), R(2), входящие в соотношения (19)-(21) вычисляются по
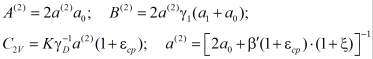(22)
Выражение (22) включает в себя основные характеристики уплотняемого массива, и оно полностью отражает физико-механические свойства грунта.
Пользуясь соотношениями (19)-(22) определены давления в поровой жидкости. Поровое давление дает возможность находить сумму главных напряжений в скелете грунта, а также вертикальные перемещения верхней поверхности уплотняемого массива.
Анализ вычислений показывает, что давление в поровой жидкости для плоской задачи меньше, чем для одномерного случая. В то же время характер изменения кривых, как для порового давления, так и для осадка и напряжений в скелете грунта остаются такими же, как для одномерного уплотнения. Задачи теории уплотнения упругоползучих неоднородных грунтов в различных постановках также исследованы авторами данной работы [2-6].
Библиографическая ссылка
Дасибеков А.Д., Юнусов А.А., Сайдахметов П.А., Омашова Г.Ш. МЕТОД ВОЗМУЩЕНИЙ В ТЕОРИИ УПЛОТНЕНИЯ УПРУГОПОЛЗУЧИХ НЕОДНОРОДНЫХ ЗЕМЛЯНЫХ МАСС // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 8-3. – С. 18-22;URL: https://applied-research.ru/ru/article/view?id=5740 (дата обращения: 21.11.2024).