Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Майер Р.В. 1

---

1 ФБГОУ ВПО «Глазовский государственный педагогический институт им. В.Г. Короленко»

С помощью метода имитационного моделирования решена проблема оптимизации распределения времени изучения различных элементов учебного материала (ЭУМ) в зависимости от их сложности. Для этого создана компьютерная модель ученика, изучающего последовательность из 100 ЭУМ различной сложности, определяющая количество знаний в конце обучения. Проводится серия испытаний, в которых варьируются длительности изучения каждого ЭУМ и решается соответствующая оптимизационная задача. При этом суммарное время обучения не изменяется. В статье приводится программа в среде Free Pascal и получающиеся графики при различных коэффициентах усвоения ученика.

Статья в формате PDF

1541 KB

дидактика

математическая теория обучения

имитационное моделирование

кибернетическая педагогика

компьютерная модель ученика

1. Кудрявцев В.Б., Вашик К., Строгалов А.С., Алисейчик П.А., Перетрухин В.В. Об автоматном моделировании процесса обучения. – Дискретная математика. – 1996. – Т. 8, вып. 4. – C. 3 – 10.

2. Леонтьев Л.П., Гохман О.Г. Проблемы управления учебным процессом: Математические модели. – Рига, 1984. – 239 с.

3. Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения. – Глазов: ГГПИ, 2013. – 138 с. (http://maier-rv.glazov.net)

4. Майер Р.В. Многокомпонентная модель обучения и ее использование для исследования дидактических систем // Фундаментальные исследования: Педагогические науки. – 2013. – № 10. – С. 2524 – 2528.

5. Майер Р.В. Основная задача математической теории обучения и ее решение методом имитационного моделирования // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 2 – С. 36–39. URL: www.rae.ru/upfs/?section=content &op=show_article&articleid=5002 (дата обращения: 27.02.2014).

6. Редько В.Г. Модели адаптивного поведения и проблема происхождения интеллекта – «Математическая биология и биоинформатика». – 2007 – том 2, N 1. – С. 160 – 180.

7. Соловов А.В., Меньшиков А.А. Дискретные математические модели в исследования процессов автоматизированного обучения // Educational Technology & Society. – 2001. – № 4. – С. 205 – 210.

1. Имитационное моделирование процесса обучения

Оптимизация учебного процесса требует разработки теоретических основ дидактики, построения математической теории обучения. В настоящее время получил распространение информационно-кибернетический подход к анализу дидактических систем, основанный на рассмотрении системы «учитель–ученик» с точки зрения теории управления. Возник и развивается новый раздел педагогики – кибернетическая педагогика, в основе которой лежит утверждение о том, что процессы обучения и воспитания во многом сводятся к управлению развитием различных качеств личности учащихся с помощью целенаправленных и согласованных воздействий со стороны учителя и родителей. Одним из важнейших направлений кибернетической педагогики является оптимизация процесса обучения, нахождение таких форм и методов организации учебного процесса, при которых функционирование системы образования было бы наиболее эффективным, то есть при наименьших затратах приносило бы максимальную пользу.

Среди современных методов исследования педагогических систем особое положение занимают методы математического и имитационного (компьютерного) моделирования. Их сущность состоит в том, что реальная педагогическая система заменяется абстрактной моделью, – некоторым идеализированным объектом, который повторяет наиболее существенные свойства изучаемой системы. При этом исследуется поведение модели с помощью математических методов [1, 2] и путем компьютерной имитации [4–7]. Последнее означает создание компьютерной программы, которая ведет себя подобно системе “учитель–учащиеся”, и проведение серии испытаний при различных параметрах, начальных условиях и внешних воздействиях. Изменяя начальные данные и параметры модели, можно исследовать пути развития системы, определить ее состояние в конце обучения. Также может быть решена оптимизационная задача [3, с. 86–90], заключающаяся в нахождении распределения учебного материала, уровня требований учителя, длительности занятий, при которых уровень знаний учащихся в конце обучения достигнет заданного значения, а сам процесс обучения будет удовлетворять наложенным ограничениям на затраты времени и усилий учеников и учителя.

Дидактическая система «учитель–ученик» является самонастраиваемой: учитель выбирает такие методы обучения, при которых ученик достигает наиболее высоких результатов. При этом он стремится минимизировать суммарные усилия P и затраты времени t на обучение, максимизируя целевую функцию – уровень знаний ученика Z. Ученик в свою очередь стремится так организовать свою деятельность, чтобы минимизировать разность между уровнем требований учителя U и уровнем приобретенных знаний Z (или выполненной работой). Определяя оптимальный путь обучения, получаем методику, по которой работает идеальный учитель.

2. Оптимизация времени изучения ЭУМ различной сложности

Допустим, учебный курс состоит из 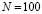элементов учебного материала (ЭУМ) 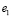, , 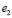..., 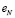, характеризующихся сложностью 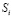из интервала [0; 1]. Если 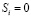, то сложность i-го ЭУМ минимальна, он очевиден для ученика. При 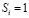сложность ЭУМ такова, что для его изучения требуется очень много времени. Рассмотрим два варианта: 1) сложность 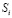– случайная равномерно распределенная величина в из интервала [0; 1]; 2) сложность 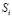равномерно растет от 0 до 1 с шагом 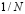по закону 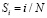. Общее время изучения T, равное сумме всех ti (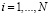) остается постоянным, коэффициент усвоения учащегося a задан. Необходимо: 1) определить оптимальные значения 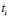длительностей изучения каждого ЭУМ, при которых уровень знаний ученика в конце обучения будет максимальным; 2) получить соответствующую зависимость уровня знаний ученика от сложности ЭУМ; 3) изучить зависимость распределения времени ti изучения ЭУМ от их сложности 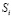при различных коэффициентах усвоения 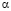и продолжительностях обучения T.

Будем исходить из того, что знания ученика 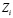: 1) увеличиваются со скоростью, пропорциональной произведению разности 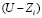на 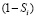; 2) вследствие забывания уменьшаются со скоростью 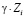. Получаем дифференциальное уравнение [3, 4]:

.

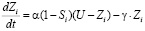Уровень требований учителя U для каждого ЭУМ равен 1. Будем считать, что знания 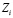i-го ЭУМ в результате обучения увеличиваются от 0 (ЭУМ совсем не изучен) до некоторого значения, не превышающего 1. Максимально возможное значение 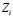равно 1, что соответствует полному изучению i-го ЭУМ. Рассматриваемое дифференциальное уравнение можно записать в конечных разностях:

.

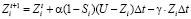Программа должна моделировать изучение первого ЭУМ в течение времени 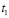, затем изучение второго ЭУМ в течение времени 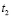и т.д., изучение N-го ЭУМ в течение времени 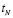(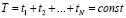). Определив уровень усвоения каждого ЭУМ, можно рассчитать суммарное количество знаний в момент t: 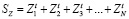и в конце обучения. Чтобы решить оптимизационную задачу, необходимо случайным образом варьировать время ti изучения i-го ЭУМ и принимать такие значения ti, при которых уровень знаний ученика в конце обучения становится выше.

Число параметров оптимизации равно N. Компьютерная программа ПР–1, решающая данную оптимизационную задачу, содержит:

1. Блок задания параметров модели, в котором задаются: 1) коэффициенты усвоения a и забывания 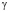ученика; 2) количество N изучаемых ЭУМ; 3) общее время обучения 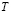; 4) сложность каждого ЭУМ 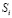, которая равномерно растет от 0 до 1 с шагом 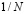по закону 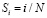либо принимает случайные значения из интервала [0; 1]; 5) начальные значения оптимизируемых переменных 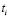(время изучения i-го вопроса). В программе ПР–1 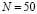, 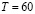УЕВ (усл. ед. времени), 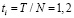УЕВ,.

2. Процедуру Obuchenie, в которой осуществляется моделирование обучения. Она, исходя из известных 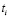, определяет уровень знаний ученика 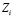по каждому i-му вопросу, а также суммарное количество знаний ученика Z по всем N вопросам в конце обучения.

3. Процедуру Grafik, которая очищает экран и строит графики: 1) зависимости 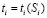времени изучения различных ЭУМ от их сложности; 2) зависимости 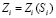количества знаний учеников для различных ЭУМ в конце обучения от их сложности .

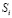Программа ПР–1

4. Цикл Repeat … until, в котором осуществляется оптимизация. В нем случайным образом выбираются 5 ЭУМ, изменяются их время изучения ti на небольшие случайные величины, пересчитываются все остальные ti так, чтобы их сумма оставалась равной T. Для этого в цикле вычисляются новые значения 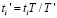, где 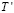– сумма всех ti после их изменений. Снова моделируется изучение N вопросов (процедура Obuchen;) и вычисляется суммарный уровень знаний 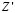. Если он оказывается выше предыдущего, то изменения принимаются, а иначе – отвергаются и все повторяется еще раз. Так продолжается до тех пор, пока суммарное количество знаний Z не достигнет максимума.

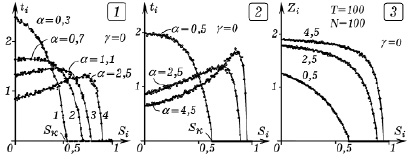
Рис. 1. Оптимальные распределения времени ti изучения ЭУМ и уровня усвоенных знаний Zi в зависимости от сложности Si при различных α ()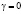

3. Результаты моделирования

В результате работы программы ПР-1 строится график зависимости времени 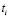изучения различных ЭУМ от их сложности 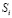, при которой суммарный уровень знаний ученика 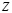в конце обучения максимален. В случае, когда 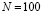, 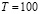УЕВ и 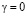, получаются кривые, изображенные на рис. 1.1 и 1.2. Для каждого α существует критический уровень сложности ЭУМ Sк; те вопросы, у которых 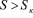, изучать не следует (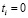). При низком коэффициенте усвоения 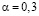нужно изучать лишь те вопросы, сложность которых невелика, затрачивая на них больше времени (рис. 1.1, кривая 1). Вопросы со сложностью 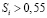изучать не следует. При увеличении α ученик быстрее усваивает информацию, поэтому время изучения простых вопросов с 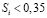уменьшается (кривые 2 и 3, соответствующие 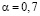и 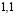), а за счет этого увеличивается круг вопросов, которые должны быть изучены (S_к растет).

При высоком коэффициенте усвоения α учащийся должен изучать почти все вопросы за исключением самых сложных (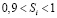), которые он все равно усвоит плохо (кривая 4, 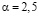). Это объясняется тем, что при 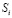, стремящимся к 1, скорость увеличения знаний 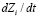уменьшается до 0, и время, требуемое для изучения данного ЭУМ, стремится к бесконечности. Для не очень сложных вопросов с 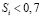, которые изучаются достаточно полно (так что после обучения 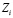близко к 1), оптимальное время изучения ЭУМ прямо пропорционально сложности ЭУМ. На рис. 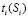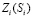1.2 и 1.3 представлены графики и при 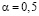, , 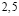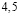. Видно, что по мере увеличения S_i уровень усвоения i-го ЭУМ уменьшается, то есть после обучения ученик простые вопросы знает лучше сложных.

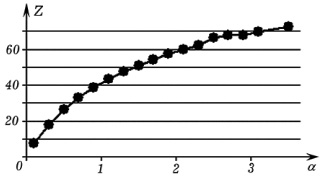
Рис. 2. Зависимость суммарного уровня знаний Z в результате оптимального обучения от коэффициента усвоения a пр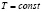и и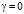

При фиксированном времени обучения T повышение коэффициента усвоения α ученика приводит к росту суммарного количества знаний Z в конце обучения. Получающийся график зависимост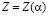и при 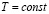, 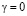и оптимальной организации обучения (распределении ti) изображен на рис. 2. Он представляет собой возрастающую кривую, которая с ростом α от 0,1 до 3,5 увеличивается от 7 до 70. Максимально возможное значение Z равно .

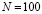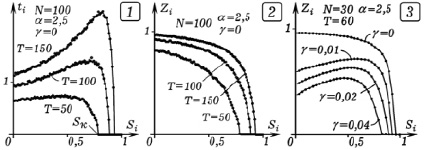
Рис. 3. Результаты оптимизации времени ti изучения ЭУМ при различных T и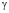

На рис 3.1 представлены результаты оптимизации времени изучения ti различных ЭУМ в зависимости от их сложности 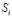в случаях, когда время изучения T равно 50, 100 и 150 УЕВ. На рис 3, 2 изображены соответствующие графики зависимости знаний 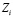ЭУМ от их сложности 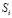. Видно, что если длительность обучения T становится меньше, то Sк снижается, то есть следует изучать простые ЭУМ с небольшой 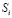, затрачивая на каждый из них меньше времени. При большой длительности обучения T (например, 150 УЕВ) критическая сложность Sк растет, график 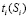сначала возрастает, а потом резко падает до 0.

На рис. 3.3 представлены графики 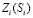при различных коэффициентах забывания γ. Видно, что при больших γ ученик успевает забыть часть информации, полученной в начале обучения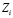, и при 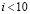становится меньше. Предлагаемая компьютерная модель позволяет решить задачу и при других параметрах модели α, γ, N, T.

Выводы

Обсуждаемая модель процесса обучения позволила исследовать зависимость оптимального распределения времени изучения отдельных вопросов (ЭУМ) от α, γ, N, T. Было установлено следующее: 1) характер распределения 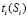сильно зависит от соотношения коэффициента усвоения ученика α, длительности обучения T и количества изучаемых вопросов N; 2) при малых коэффициентах усвоения α имеет смысл изучать только простые ЭУМ, добиваясь высоких знаний для ЭУМ с 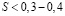; 3) при высоком коэффициенте усвоения α следует изучать ЭУМ, имеющие сложность 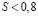, причем на более сложные ЭУМ необходимо затрачивать больше времени, чем на менее сложные; 4) при уменьшении длительности обучения T нужно ограничиться изучением ЭУМ с низкой сложностью; 5) при отсутствии забывания распределение уровня знаний ученика от сложности ЭУМ характеризуется убывающей функцией 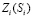; 6) если имеет место забывание, то уровень владения учащимся ЭУМ с низкой сложностью (которые изучались вначале) снижается. Полученные результаты соответствуют основным положениям теории обучения.

Библиографическая ссылка