Известо, что при изложении основных закономерностей квантовой механики, математического аппарата микромира, соотношении неопределенностей Гейзенберга, волновых функций, вероятности нахождения микрочастицы у студентов ВУЗа возникают определенные трудности с освоением новых материалов по квантовой механике. В первую очередь возникнуть сомнения относительно точности определения координат микрочастицы. Во-первых попробуем разобраться с понятием микрочастицы, что означает само слово микрочастица. При вводной лекции по квантовой механике по аналогии с оптикой, где свет имеет двойственную природу, корпускулярно-волновой дуализм света, эта двойственная природа света переносится также на любую частицу в микромире. Например рассмотрим электрон, что он собой представляет, эта частица или волна? При таком вопросе студент не знакомый с квантовой теорией затрудняется ответить точно, в принципе в квантовой механике на этот вопрос ответ будет следующий: электрон- это микрочастица со специфическими свойствами, в одних явлениях он демонстрирует корпускулярные свойства, а в других явлениях он демонстрирует волновые свойства. Вот это точное определение свойственное квантовой теории! Значит двойственную природу света можно смело переносить и на любую частицу в микромире, т.е. на микрочастицу.
Дифракционную картину на экране можно наблюдать не только от естественного света но и от отдельных частиц, например от электронов, протонов и т.д. Отсюда сразу становится ясно, что каждая микрочастица также обладает корпускулярно-волновыми свойствами как и свет.
Теперь попробуем разобраться с точностью определения координаты и вероятностью нахождения микрочастицы в определенной области микромира. Здесь мы должны непременно обьяснить студентам, что в микромире встречаются такие явления, которые не имеют аналогов в классической механике, например явления туннельного эффекта, т,е эффект просачивания электронов через потенциальный барьер. Суть туннельного эффекта заключается в том, что микрочастица летящая с определенной скоростью, с определенной энергией Е к потенциальному барьеру с энергией U, при случае когда энергия микрочастицы меньше высоты потенциального барьера она имеет вероятность прохождения через потенциальный барьер, когда энергия микрочастицы больше высоты потенциального барьера, она может и отскочить от потенциального барьера в обратную сторону.
Вот это явление никак не укладывается в теорию обычной классической механики, поэтому мы говорим, что оно не имеет классического аналога, в целом в квантовой механике имеются и другие явления которые не могут быть обьяснены с точки зрения классической теории.
Теперь рассмотрим координату электрона например, в классической механике мы сможем точно указать координату и импульс электрона, а в квантовой теории они задаются с определенной вероятностью, согласно соотношению неопределенностей Гейзенберга, т.е.
;
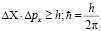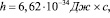
Чем точнее мы хотим определить координату частицу,тем больше мы ошибаемся в определении импульса частицы, и наоборот, чемточнее мы хотим определить импульс частицы, тем больше мы ошибаемся в определении координаты частицы. Вот эти параметры: координата и импульс определяются с точностью до постоянной Планка, а это означает тридцать четыре нуля после запятой, более точнее определить эти параметры не возможно, это заложено самой природой микрочастиц! Имеется еще и другое соотношение неопределенностей Гейзенберга, аналогичное для энергии и времени, здесь точность определения такое же как в вышеуказанном случае.
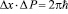
ΔtΔE = 2πh
Вот здесь мы должны детально обьяснить физическую природу определения параметров электрона, во-первых, естественно точность определения параметров не может быть бесконечной, об этом мы говорили когда сказали про постоянную Планка. Во-вторых, определение любых параметров измеряется с помощью приборов, эти приборы тоже состоят из атомов, электронов, протонов, нейтронов,других частиц, а соотношение неопреленностей Гейзенберга заложено в самой природе этих частиц!
Значит квантовая механика, в отличие от классической механики в определении параметров микрочастицы пошла еще дальше, еще глубже она установила причинно-следственную связь, выяснила глубокий философский смысл физической природы микрочастиц, если соотношение неопределенностей Гейзенберга в классической физике приводится как интуитивно полученное выражение, а в квантовой теории оно теоретически получается из законов микромира сложными математическими преобразованиями. В данной статье доказательства соотношения неопределенностей Гейзенберга не ставилась нам самоцелью, она имеется во многих литературах по квантовой механике [1–3].
Теперь попытаемся разобраться определением вероятности нахождения микрочастицы в заданном обьеме. В микромире квантовая частица может находиться в определенном обьеме, в момент времени t, вокруг радиуса вектора rс равной вероятностью в любой точке пространства. Вероятность нахождения микрочастицы определяется согласно следующему определению:
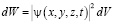
где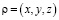 
– плотность вероятности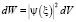 
Значит движение электронов точно описывает теория вероятностей.
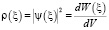
В квантовой механике рассматривается определенная модель бесконечно глубокой потенциальной ямы, где может находиться микрочастица. Для этой микрочастицы решается уравнение Шредингера для одномерного случая, из этого уравнения находим волновые функции и значения энергии, которые являются собственными функциями и собственными значениями оператора. Здесь мы не будем подробно останавливаться на решение этого уравнения, математических расчетах и т.д., рассмотрим только полученный конечный результат, сделаем выводы. Для того, чтобы показать насколько квантовая механика точно определяет вероятность нахождения микрочастицы в данной потенциальной яме потенциальную яму разделим по вертикали на несколько частей. Если потенциальную яму разделим на 2 части, тогда вероятность нахождения должна быть W = 0,5, а если на 5 частей тогда W = 0,2, а если потенциальную яму разделит на 20 частей, тогда W = 0,05. Математически все таки должно быть. В квантовой механике когда находим вероятности нахождения микрочастицы в данной потенциальноя яме, тогда выполнения интеграла по формуле мы точно получаем все эти значения с точностью до одной сотой после запятой. Рассмотрим следующую задачу:
Задача 1. Электрон расположен в бесконечно глубокой прямоугольной потенциальной яме. Ширина ямы равноl. Определить вероятность того, что электрон в возбужденном состоянии находиться (n = 3) в одной трети части потенциальной ямы.
Решение:
Напишем стационарное уравнение Шредингера для электрона находящегося в бесконечно глубокой прямоугольной потенциальной яме:
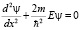
Ее решение
, 
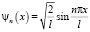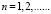
В возбужденном состоянии n = 3
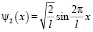
соответствует такая собственная функция. Квадрат этой собственной функции определяет вероятность нахождения частицы в данной точке пространства, значит
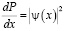отсюда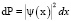 
Вероятность нахождения электрона в данной точке будет следующая:
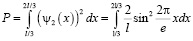
Интегрируем последнее полученное выражение:
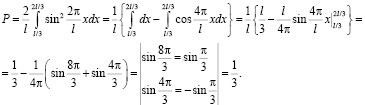
Вот здесь наглядно видно точность и триумф квантовой механики, самой красивой теории теоретической физики!
Одним словом квантовая механика в отличие от классической механики наглядно и точно, детально описывает физические процессы протекающие в микромире.
Библиографическая ссылка
Абекова Ж.А., Оралбаев А.Б., Ермаханов М.Н., Орманова А.А. ОСОБЕННОСТИ ИЗЛОЖЕНИЯ ОСНОВ И ТОЧНОСТИ КВАНТОВОЙ МЕХАНИКИ ПРИ РЕШЕНИИ ЗАДАЧ МИКРОМИРА // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 10-2. – С. 31-33;URL: https://applied-research.ru/ru/article/view?id=5991 (дата обращения: 19.04.2024).