Производственная функция (production function) – формализованное соотношение, связывающее количество производимой продукции и факторы производства, в качестве которых рассматриваются труд и капитал. Производственная функция используется для описания различных экономических единицы: предприятий, отраслей, народнохозяйственной системы в целом. В последние годы появились работы, посвященные использованию производственных функций и в региональных исследованиях. Однако, использование производственных функций в региональных измерениях, как правило, требовало адаптации методических схем не только под методологические ограничения, вызванные задачами исследований, но и под возможности статистической базы [1, 2, 5]. О плодотворном использовании этих функций в описании региональных процессов говорят результаты исследований, в том числе и авторских, позволяющие отобразить специфику региональных производственных процессов каких-либо регионов, выявить тенденции и закономерности производства ВРП в конкретных регионах и региональных группах [см., напр.: 1, 3, 7, 10]. Как показывают исследования, особенное значение имеют выявленные особенности производства ВРП для формализованного отображения проблемы межрегиональной дифференциации экономического пространства России [2, 6, 8, 9, 10]. В целом, следует заключить, что тематика производственных функций достаточно широка, что предполагает обозначение вопросов, которые будут рассмотрены в настоящей работе.
Цель работы преследует рассмотрение следующих вопросов. Во-первых, истории развития производственных функций. Во-вторых, рассмотрение современного классического понимания производственной функции и ее применения для целей региональных исследований.
История развития производственных функций. Как отмечал автор в предшествующих работах [см., напр.: 2], наиболее комплексное критическое изложение специфики и сущностных оснований развития производственных функций приведено в фундаментальном труде Марка Блауга «Экономическая мысль в ретроспективе».
В частности, здесь обсуждаются квадратичная производственная функция рикардовской системы [4, С.95-98]. Затем приводятся бесплодные попытки доказательства Уикстида («Очерк о согласовании законов распределения»), что совокупный продукт в точности сводится к возмещению издержек каждого из производственных факторов в соответствии с их предельной производительностью, и доказательство этого утверждения Флаксом [4, С.408–409].
Несомненный интерес для познания сущности производственных функций представляет обсуждение обозначенной Флаксом связи проблемы исчерпанности продукта с теоремой Эйлера об однородных функциях [4, С. 409–410]. А затем, когда читатель уже уверует в утверждение о том, что производственная функция имеет линейно-однородный вид, что более высокая или низкая степень однородности не имеют экономического смысла, М. Блауг приводит формальные свойства подобных функций с одновременной фиксацией серии предостережений относительно ряда экономических показателей [4, С.411–419].
Обобщая формальные свойства, приводятся аргументированные фундаментальные утверждения.
Во-первых, предельный продукт какого-либо фактора варьирует только при изменении относительных количеств применяемых факторов.
Во-вторых, эти факторы обладают комплементарностью, т.е. увеличение количества переменного фактора снижает его предельную производительность, но увеличивает предельную производительность фиксированного производственного фактора.
В-третьих, совокупный продукт в точности складывается из выплат используемым производственным факторам в соответствии с их предельной производительностью.
Но все эти утверждения справедливы только для производственных функций типа Кобба-Дугласа. Из этого следует важный методологический вывод – если показатели эластичности оцениваются исходя из относительных долей производственных факторов, которые в сумме составляют совокупный доход, то предполагается, что такая производственная функция имеет вид функции Кобба-Дугласа.
Что касается экономического смысла линейно-однородных производственных функций, то справедлив тезис – только когда производственная функция линейно однородна, выплаты производственным факторам в соответствии с предельной производительностью полностью исчерпают продукт.
Но, далее формулируется вопрос – если производственная функция не является однородной первой степени? В принципе, подразумевается, что конкуренция на рынках факторов производства обеспечивает оплату производственных факторов в размере их предельной ценности или предельного продукта в денежном выражении вне зависимости от типа производственной функции. Но, если производственная функция не является линейно однородной первой степени, то совокупный продукт либо превысит, либо будет меньше суммы долей при распределении. Очевидно, что в случае отрицательного эффекта масштаба сумма факторных выплат, определенных характером рыночного механизма, будет меньше ценности выпущенной продукции, а остатки присваиваются некоторым «фиксированным» факторам. В случае положительного эффекта масштаба совокупный продукт оказывается недостаточным для оплаты вклада всех факторов в соответствии с их предельной производительностью. То есть, какой-то фактор должен получить меньше, чем его предельная производительность.
Эти утверждения объясняются связью между предельными и средними издержками. Линейно-однородная производственная функция образует горизонтальную долгосрочную кривую средних издержек. В случае возрастающей отдачи или снижающихся издержек в долгосрочном периоде кривая предельных издержек лежит ниже долгосрочной кривой средних издержек. В этом случае экономическая единица (фирма) начинает нести убытки, поскольку оплата фактора согласно его предельному продукту есть результат действия механизма ценообразования, основанного на предельных издержках.
Эти рассуждения служат основой тезиса Хотеллинга-Лернера – ценообразование на основе предельных издержек во всех отраслях экономики потребовало бы субсидий для любой отрасли со снижающейся ценой предложения. При этом, как справедливо подчеркивается, – «положительный эффект масштаба уничтожает конкуренцию и, следовательно, основу для оплаты факторов в соответствии с их предельной производительностью. Подобным образом, цена, покрывающая долгосрочные предельные издержки в случае, когда последние превышают долгосрочные средние издержки, обязательно приведет к образованию остатка» [4, С. 419].
Такой подход к рассуждениям о сущностных основаниях производственных функций позволяет затрагивать важнейшие смежные сферы экономических знаний, тем самым, позволяя комплексно освещать экономические процессы. На взгляд автора, этот аспект чрезвычайно важен для процесса обучения экономике студентов, направленного на формирование у студентов метода познания экономических проблем. Нередко, к сожалению, подменяемого формальным заучиванием значительного количества фактов, теорий, без структурного взаимопроникновения знаний.
К сожалению, в большинстве учебников по экономической теории, по истории экономических учений и т.д. производственные функции если и обсуждаются, то крайне скупо. Наиболее четко производственные функции проявляются в учебниках по дисциплинам близким к прикладной математике – математической экономике, эконометрике, математическим методам и моделям в экономике и т.п.
Следует отметить, в отличие от того же Блауга, в учебниках по этим дисциплинам математическое изложение производственных функций более оптимальное [см., напр.: 5, С. 14–26]. Но при этом отсутствует «сопряжение» с рядом базисных понятий экономической теории. Конечно, с одной стороны, это закономерно, поскольку учебники носят достаточно узкодисциплинарный характер. С другой стороны, опыт работы автора над реальными экономическими задачами методами математического моделирования указывает на проблему, нередко, избыточного применения упрощающих предпосылок, влекущего выхолащивание смысла экономических категорий, или увлечения математической стороной описания в ущерб задачи реалистичности представления экономического объекта (процесса). Другая проблема – при обучении студентов возникает необходимость не только объяснения конкретных задач в рамках производственных функций, но и объяснения связей с фундаментальными понятиями и экономическими законами, которые студенты успешно забыли позабыть. Это проблема диктуется не только временным разрывом между преподаванием дисциплин экономической теории и эконометрики, но также нередким отсутствием необходимой сопряженности предметов между собой.
Классическая производственная функция и пример ее использования в региональных исследованиях. Напомним, классической поход к моделированию производственных процессов с помощью производственных функций состоит в использовании динамических рядов исследуемой экономической системы, характеризующих выпуск продукции в виде объемов производства за определенные промежутки времени и используемые для этого ресурсы (труд и капитал), для оценивания параметров производственной функции. Сама производственная функция выражает зависимость результата производства от затрат ресурсов. Показательная производственная функция имеет вид:
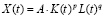 ,
,
где X(t) – выпуск продукции за период t; K(t) – капитал за период t; L(t) – труд за период t.
Остальные переменные (A, p и q) являются оцениваемыми параметрами и при логарифмировании соотношения могут быть определены методом наименьших квадратов.
При этом А всегда больше нуля и называется коэффициентом нейтрального технического прогресса (при постоянных p и q выпуск в точке (K, L) тем больше, чем больше A), p – эластичностью[1] по фондам, q – эластичностью по труду.
Напомним, экономический смысл эластичности заключается в том, что при увеличении соответствующего фактора на 1 %, результат увеличится на количество процентов, равных значению эластичности. Имея достаточные по длине динамические ряды можно с помощью уравнения функции связать выпуск продукции, капитал и труд.
Используемые показатели. Предшествующие исследования позволили охарактеризовать зависимость производства ВРП субъектов Российской Федерации от основных фондов и количества занятых в экономике [подробнее см.: 1, 2]. То есть, за выпуск X(t) принимался ВРП за год; за K(t) – капитал (стоимость основных фондов) за год t; за L(t) – труд (количество занятых в исследуемой системе) за год t.
В настоящее время автором разработаны модели для трех региональных групп:
- группа регионов всей России: 82 субъекта – все субъекты Российской Федерации (за исключением Чеченской республики по причине неполноты исходных статистических данных, Республики Крым и г.Севастополя по причине недавнего вхождения в состав Российской Федерации, исключающего целесообразность рассмотрения предыстории субъектов иного государства);
- группа субъектов зоны Севера России, территории которых полностью включены в зону Севера: 13 субъектов (Мурманская область, Республика Карелия Архангельская область, Ненецкий автономный округ (АО), Чукотский АО, Камчатский край, Сахалинская область, Магаданская область, Ямало-Ненецкий АО, Ханты-Мансийский АО – Югра, Республика Коми, Республика Саха (Якутия), Республика Тыва);
- группа несеверных регионов: 69 субъектов – регионы Российской Федерации без группы субъектов зоны Севера России.
Однако в новых моделях изменены показатели. Рассмотрено два варианта. В первом варианте составляющие модели производственной функции характеризуются показателями: выпуск – индекс физического объема ВРП субъектов Российской Федерации; ресурс труда – индекс среднегодовой численности занятых в экономике субъектов Российской Федерации; ресурс капитала – индекс физического объема основных фондов экономики (все индексы приведены к 2000 г.). Во втором варианте: выпуск – индекс физического ВРП субъектов Российской Федерации; ресурс труда – индекс среднегодовой численности занятых в экономике субъектов Российской Федерации; ресурс капитала – индекс физического объема инвестиций в основной капитал (все индексы также приведены к 2000 г.).
Рассмотрение этих двух вариантов позволило автору ответить на вопрос: от чего зависит производство ВРП субъектов Российской Федерации – от основных фондов (то есть, фактически от накопленного капитала) или от инвестиций? Особенный интерес представляло рассмотрение этого вопроса для субъектов Севера России в условиях ожидаемой интенсификации инвестиционных процессов на этих территориях.
Полученные результаты этого исследования будут в ближайшее время приведены в статьях журналов открытого доступа в Интернете. А сейчас вернемся к рассмотрению методических особенностей использования производственных функций в региональных исследованиях.
Упрощающие предпосылки, гипотезы и варианты интерпретации. Для применения производственной функции в региональных исследованиях необходимо сделать упрощающие предпосылки и выдвинуть гипотезы.
Будем считать, что экономика всех субъектов РФ функционируют в одном правовом поле и по одним и тем же принципам.
Будем считать, что с точки зрения производства ВРП экономики регионов внутри одной региональной группы отличаются лишь количествами основных фондов и труда.
Последняя гипотеза проверяется при оценивании параметров производственной функции. При этом возможны три случая, приводящие к различной интерпретации [подробнее см.: 1, 5].
Первый случай. При оценивании параметров производственной функции получилось – малое значение коэффициента детерминации, большая ошибка аппроксимации и условия F-критерия не выполнены. Это означает, что модель производства ВРП не соответствует данным региональной статистики и гипотеза о том, что ВРП регионов внутри региональной группы зависит лишь от труда и капитала неверна.
Второй случай. Производственная функция достаточно хорошо согласуется с региональными данными и оцененные значения параметров лежат в допустимых пределах, т.е. 0 < p, q < 1. В этом случае производственная функция является неоклассической [5, С.15] и производство ВРП в изучаемой региональной группе удовлетворяет следующим условиям:
- с ростом ресурсов выпуск растет
- (
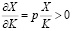 ,
, 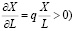 ;
; - с ростом затрат ресурса предельная отдача (частная производная выпуска по ресурсу) падает, т.е. при увеличении количества вовлекаемого в производство ресурса скорость роста выпуска уменьшается;
- если p > q, рост выпуска ВРП является трудосберегающим (интенсивным), если p < q, то фондосберегающим (экстенсивным);
- при p + q > 1 ВРП растет быстрее, чем в среднем растут капитал и труд, т.е. производственная функция описывает растущую экономику, в противном случае – стагнирующую; значение этой суммы является количественной характеристикой экономического роста.
Третий случай. Производственная функция достаточно хорошо согласуется с региональными данными, но оцененные значения параметров выходят за допустимые пределы. Возможные варианты этого случая в работах [1, 2, 5]
Либо p < 0, либо q < 0 – с ростом либо капитала, либо труда выпуск ВРП падает. Это означает, что в региональной группе имеет место тенденция, когда меньшие ресурсы приводят к большему выпуску ВРП. Это свойство характерно для экономик регионов с меньшим количеством населения, которые производят больший ВРП (в удельном исчислении).
Либо p > 1, либо q > 1 – с ростом затрат либо капитала либо труда предельная отдача растет (при увеличении количества вовлекаемого в производство ресурса скорость роста выпуска увеличивается). Автор затрудняется дать интерпретацию этому случаю. Скорее всего, это свойство характеризует не установившуюся (переходную) экономику или экономику, выходящую из кризиса. Как показывают исследования автора, ряд регионов Севера имеет такие характеристики [1].
При соответствии модели реальным данным оценить влияние труда и капитала на производство ВРП можно рассчитав удельные веса соответствующих эластичностей: p*100 %/(p + q), q*100 %/(p + q).
Из двух региональных групп более интенсивную (более экстенсивную) экономику имеет та из них, у которой удельный вес эластичности по капиталу больше (меньше).
Таким образом, оценив параметры производственной функции за различные годы, мы можем охарактеризовать динамику производства ВРП в РФ.
В заключение отметим, производственные функции являются моделями, исследование которых многократно показывало целесообразность их использования в экономических исследованиях. Современные задачи региональной экономики и методический потенциал производственных функций позволяют плодотворно использовать их для исследования региональных производственных процессов. При этом регионы рассматриваются как целостные, неструктурированные единицы, на вход поступают ресурсы, а на выходе получается результат функционирования экономики в виде ВРП.*
*Публикация подготовлена в рамках поддержанных научных проектов: РФФИ № 13-06-00030, РГНФ и Правительства Мурманской области №14-12-51005, РГНФ № 14-02-00128.
[1] Экономический смысл эластичности заключается в том, что при увеличении соответствующего фактора на 1 %, результат увеличится на количество процентов, равных значению эластичности.
Библиографическая ссылка
Баранов С.В. ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ: ИСТОРИЯ И СОВРЕМЕННОСТЬ // Международный журнал прикладных и фундаментальных исследований. 2014. № 10-2. С. 53-57;URL: https://applied-research.ru/ru/article/view?id=5996 (дата обращения: 12.03.2026).

