Металломатричные композиты (ММК) обладают улучшенными свойствами по сравнению с неармированными монолитными металлическими аналогами. Они имеют высокую прочность, жесткость, износостойкость, теплопроводность, повышенное сопротивление при высокотемпературных нагрузках и сопротивление на усталость, низкую плотность и коэффициент теплового расширения.
В этих материалах металл выступает в качестве матрицы, которая усиливается путем добавления неметаллических веществ, обычно керамики. При создании ММК возможно целенаправленное изменение их механических и эксплуатационных свойств путем подбора состава, изменения соотношения компонентов и методов изготовлениям композита. В результате эти композиционные материалы имеют разные приложения в ряде отраслей, включая автомобилестроение, электротехническую и аэрокосмическую промышленность. Из них изготавливаются детали двигателей внутреннего сгорания, тормозных систем, элементы транспортных, авиационных и ракетных конструкций, тепловые части управления силовой электроники, спортивные товары.
Исследования проводятся по изучению сопротивления деформации [1–4], влиянию режимов обработки на формирование микроструктуры [2, 5], построению моделей сопротивления деформации при горячей пластической деформации [3, 4, 6–9]. В работах [2–4, 8] показано, что для некоторых металломатричных композитов на основе алюминия форма кривых сопротивления деформации композита сильно зависит от скорости деформации. Так в металломатричном композите 15 % SiC/Al при температурах 450 °С и 500 °С в диапазоне скоростей деформаций 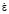 = 5–10 с-1 сопротивление деформации σS имеет максимальный пик напряжения деформирования, после которого сопротивление деформации падает с увеличением степени деформации [3]. При этих же температурах, но при
= 5–10 с-1 сопротивление деформации σS имеет максимальный пик напряжения деформирования, после которого сопротивление деформации падает с увеличением степени деформации [3]. При этих же температурах, но при 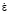 = 0,1 – 1 с-1 сопротивление деформации не имеет максимального пика и значение сопротивления деформации постоянно растет с увеличением степени деформации. Предложенная модель сопротивления деформации в работе [3], по мнению авторов работы, недостаточно точно описывает реологическое поведение композита, что может быть связано отсутствием в модели учёта барьерного эффекта блокирования свободных дисклокаций примесными атомами и частицами SiC. В ранних работах авторов была разработана и апробирована модель сопротивления деформации на ряде сталей и алюминиевых сплавов, которая учитывает динамическую рекристаллизацию и возврат [10–12]. Структура модели позволяет добавить внутренние переменные, отвечающие за процессы, связанные упрочнением за счет барьерного эффекта.
= 0,1 – 1 с-1 сопротивление деформации не имеет максимального пика и значение сопротивления деформации постоянно растет с увеличением степени деформации. Предложенная модель сопротивления деформации в работе [3], по мнению авторов работы, недостаточно точно описывает реологическое поведение композита, что может быть связано отсутствием в модели учёта барьерного эффекта блокирования свободных дисклокаций примесными атомами и частицами SiC. В ранних работах авторов была разработана и апробирована модель сопротивления деформации на ряде сталей и алюминиевых сплавов, которая учитывает динамическую рекристаллизацию и возврат [10–12]. Структура модели позволяет добавить внутренние переменные, отвечающие за процессы, связанные упрочнением за счет барьерного эффекта.
Целью данной работы является описание реологического поведения металломатричного композита 15 % SiC/Al с помощью модели сопротивления деформации, учитывающей динамический возрат и разекристаллизацию, а также барьерный эффект блокирования свободных дислокаций при температурах 450 °С и 500 °С в диапазоне скоростей деформаций 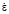 = 0,1 – 10 с-1.
= 0,1 – 10 с-1.
Модель сопротивления деформации
В качестве математической модели сопротивлении деформации была взята математическая модель из работы [10], учитывающая упрочнение за счет приращения плотности дислокаций, а разупрочнение за счет прохождения динамической рекристаллизации и возврата. Поскольку в высоколегированных алюминиевых сплавах с большим количеством включений может наблюдаться барьерный эффект блокирования границ зерен, субзерен и сводных дисклокаций [13–16], то в модель сопротивления деформации были дополнительно введены внутренние параметры, отвечающие за блокирование движения свободных дислокаций примесными атомами и включениями. Модель сопротивления деформации имеет следующий вид:
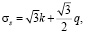
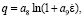
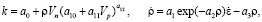
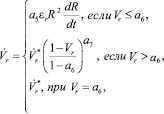
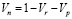 ,
, 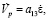
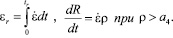
Здесь σs – напряжение сжатия (растяжения) при одноосном напряженном состоянии (сопротивление деформации); a0 = k(t0), t0 – момент времени начала пластической деформации; q – функция, описывающая вязкие свойства материала; ρ - величина, пропорциональная приращению плотности дислокаций за счет пластической деформации; εr – степень деформации, накопленная до начала динамической рекристаллизации; Vn, Vr – нерекристаллизованная и рекристаллизованная доли объема металла, соответственно; Vp – приращение объема, характеризующего скопления дислокаций, заблокированных включениями и примесными атомами; R – радиус рекристаллизованного зерна, R(tr) = 0, tr – момент времени начала динамической рекристаллизации, определяемый условием ρ = a4; ai (i = 0,…,13) – параметры модели, подлежащие идентификации по опытным данным. Объем Vn, Vr и Vp должны удовлетворять следующему равенству: 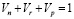 . В начальный момент времени до деформации Vn = 1, Vr = 0, Vp = 0.
. В начальный момент времени до деформации Vn = 1, Vr = 0, Vp = 0.
Модель сопротивлении деформации идентифицировали с использованием кривых сопротивления деформации металломатричного композита 15 % SiC/Al, взятых из работы [3]. В этой работе в качестве матричного материала использовался алюминиевый сплав (Cu – 4,1; Mg – 0,64; Mn – 0,54; Fe – 0,37; Si – 0,34; Zn – 0,1; Ti – 0,019; Al – ост., % по массе). К данному сплаву в объеме 15 % был добавлен порошок из SiC с размером частиц 12 мкм. Исходная микроструктура образцов приведена на рис. 1.

Рис. 1. Исходная микроструктура композита SiC/Al [3]
Результаты идентификации
На рис. 2 маркерами приведены экспериментальные значения сопротивления деформации композита 15 % SiC/Al при температурах испытаний 450 °С и 500 °С, взятые из работы [3].
Параметры модели нашли, минимизируя одновременно по четырем экспериментальным кривым сопротивления деформации для каждой температуры в отдельности среднеквадратичное отклонение расчетных значений сопротивления деформации σs(t)от экспериментальных z(t)
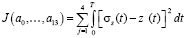 ,
,
где T – время деформации образца. Результаты идентификации модели сопротивления деформации приведены на рис. 2 сплошными линиями. Коэффициенты модели приведены в таблице.
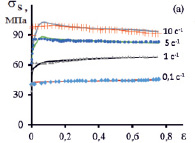
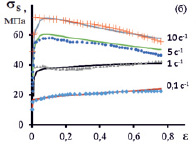
Рис. 2. Зависимость сопротивления деформации σS от степени деформации ε металломатричного композита при температуре 450 °С и 500 °С. Маркерами показаны экспериментальные зависимости из работы [3], сплошные кривые построены по результатам идентификации модели сопротивления деформации
Коэффициенты модели сопротивления деформации
|
T, °C |
a0 |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
a13 |
|
450 |
8 |
4373 |
0,12 |
62 |
5,7 |
117 |
0,144 |
1,63 |
29 |
0,36 |
0,68 |
149 |
2,05 |
0,019 |
|
500 |
6 |
4589 |
0,15 |
57 |
4,3 |
137 |
0,044 |
1,14 |
14 |
1,02 |
0,91 |
140 |
3,49 |
0,005 |
Обсуждение результатов идентификации модели
Как видно из рис. 2 поведение композита можно разделить на два типа в зависимости от скорости деформации. Материал упрочняется при скоростях деформаций 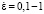 с-1, а при скоростях деформаций
с-1, а при скоростях деформаций 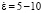 с-1 композит имеет максимальный пик напряжения деформирования, после которого происходит разупрочнение материала. Такое реологическое поведение модель сопротивления деформации учитывает, и из расчетных кривых сопротивления деформации видно, что модель достаточно хорошо описывает разупрочнение и упрочнение материала.
с-1 композит имеет максимальный пик напряжения деформирования, после которого происходит разупрочнение материала. Такое реологическое поведение модель сопротивления деформации учитывает, и из расчетных кривых сопротивления деформации видно, что модель достаточно хорошо описывает разупрочнение и упрочнение материала.
Среднее относительное отклонение d экспериментальных кривых от рассчитанных составило 2 % для температуры испытания 450 °С и 3 % для температуры испытания 500 °С. Величину δ вычисляли по формуле
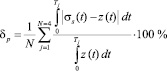 ,
,
где j – номер эксперимента; N– общее количество опытов во всех экспериментах, используемых при идентификации; Tj– время деформации образца для j-го эксперимента; z и σs – экспериментальное и полученное по результатам идентификации модели сопротивления j-го эксперимента значение сопротивления деформации.
Выводы
Из результатов идентификации модели сопротивления деформации по известным из литературы опытным данным можно заключить, что предложенная модель сопротивления деформации с достаточно хорошей инженерной точностью описывает реологическое поведение металломатричного композита 15 % SiC/Al при высокотемпературной пластической деформации при температурах 450 ºС и 500 ºС для диапазона скоростей деформаций от 0,1 до 10 с-1.
Работа выполнена при финансовой поддержке РНФ (проект №14-19-01358).
Библиографическая ссылка
Смирнов А.С., Коновалов А.В., Муйземнек О.Ю. МОДЕЛИРОВАНИЕ СОПРОТИВЛЕНИЯ ДЕФОРМАЦИИ МЕТАЛЛОМАТРИЧНОГО АЛЮМИНИЕВОГО КОМПОЗИТА 15 % SiC/Al ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ // Международный журнал прикладных и фундаментальных исследований. 2014. № 11-1. С. 22-25;URL: https://applied-research.ru/ru/article/view?id=6066 (дата обращения: 28.12.2025).

