Задача прогнозирование электропотребления не теряет своей актуальности на протяжении уже многих лет. Прежде всего это связано с особенностями функционирования электроэнергетических систем (ЭЭС), для которых точно построенный прогноз является залогом их эффективной и надежной работы.
Для задачи прогнозирования важным является отслеживание характера и расположения локальных особенностей временного ряда (ВР), описывающего потребление электроэнергии. Такими особенностями могут быть дневной и вечерний пик нагрузки, суточные перепады нагрузки, содержащие высокочастотные флюктуации, обусловленные не только шумами, но и различными изменениями режимных параметров ЭЭС.
Методика построения системы прогнозирования
Одним из наиболее эффективных инструментов выявления локальных особенностей является вейвлет-анализ, обладающий возможностями как частотной, так и временной локализации сигнала.
Предлагается ввести в модель прогнозирования предварительную фильтрацию данных с целью выделения разночастотных составляющих в динамике временного ряда и прогнозирования каждой такой составляющей в отдельности.
Общая структура системы прогнозирования приведена на рис. 1.
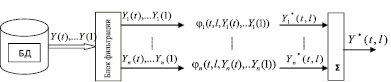
Рис. 1. Общая структура системы прогнозирования
Прогноз можно представить как
Y*(t, l) = φ(t, l, Y(t), Y(t – 1),...,Y(2), Y(1)),
где интервал [t,t+1] – интервал упреждения, l – длина интервала упреждения, Y*(t, l) − прогноз, φ − прогнозирующая функция, она зависит от количества наблюдений t, длины l и наблюдений Y(1),Y(2),…Y(t). Именно эта функция определяет метод прогнозирования [3].
Полученные прогнозы 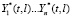 для разночастотных составляющих затем суммируются, чтобы получить итоговое прогнозное значение.
для разночастотных составляющих затем суммируются, чтобы получить итоговое прогнозное значение.
Непрерывное прямое вейвлет-преобразование обладает большой избыточностью, что приводит к большим временным затратам при его выполнении. С учетом того, что ВР, поступающий для анализа, является дискретным, альтернативой является быстрое вейвлет-преобразование (БВП).
Главным достоинством реализованной в алгоритме БВП процедуры децимации является то, что используется лишь необходимое количество информации для полной реконструкции сигнала и восстановление возможно с любой заданной точностью.
Однако в процедуре децимации есть и недостатки, главным из которых является зависимость результатов разложения от временного сдвига. Это означает, что при смещении во ВР, подлежащему вейвлет-разложению, даже на один отсчет, результаты всего разложения изменятся. В таких условиях восстановление сигнала по вейвлет-разложению в данный момент времени не является однозначным и прогнозирование невозможно.
Во избежание этой проблемы необходимо исключить операцию децимации из процедуры вейвлет-разложения. Таким образом, мы приходим к так называемому избыточному дискретному вейвлет-преобразованию (ИДВП). Для реализации ИДВП используется алгоритм «Избыточный Хаар» (алгоритм a trous) [5].
Важно то, что на каждом этапе разложения используется только информация о прошлых значениях, т.е. отсутствует «подглядывание» в будущее. На рис. 2 показано, какие отсчеты ВР используются для расчета коэффициентов для различных уровней разложения.
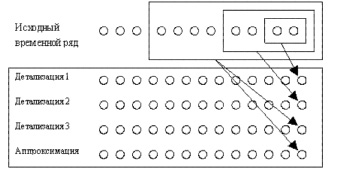
Рис. 2. Отсчеты исходного сигнала необходимые для расчета последних коэффициентов вейвлет-разложения на разных уровнях
Выбор вейвлета Хаара обусловлен, прежде всего, возможностью построения ИДВП преобразования и видом его psi-функции, что позволяет более точно воспроизводить перепады уровня электропотребления в анализируемом ВР.
Выбор глубины разложения p определяется эмпирически исходя из анализа исходного ВР и вида временных последовательностей, полученных в результате вейвлет-преобразования, либо путем анализа показателя Хёрста [4]. Проведенные исследования показали, что для анализируемого временного ряда электропотребления, характеризующегося показателем Хёрста в интервале от 0,71 и выше, наилучшая глубина разложения равная трем, для интервала от 0,65 до 0,70 – 4 и 5 и для интервалов ниже 0,65 глубина разложения должна быть от шести и выше [2].
В тоге ВР разбивается на несколько временных рядов описывающие уровень аппроксимации и детализации сигнала в сумме дающие исходный ВР. Например, для глубины разложения равной трем:
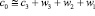 ,
,
где с0 – исходный ВР, с3 – ВР уровня аппроксимации; w3, w2, w1 – ВР уровней детализации 3, 2 и 1 соответственно.
Результаты разложения с глубиной погружения p = 3 приведены на рис. 3.
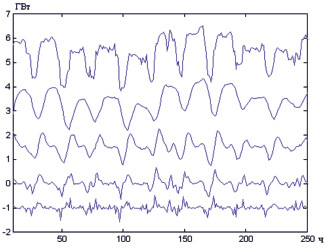
Рис. 3. Результаты вейвлет-разложения «Избыточный Хаар» для данных по электронагрузке с уровнем детализации p = 3 (сверху вниз – исходный ВР, ВР уровня аппроксимации, детализации 3, 2 и 1)
Данный подход позволяет строить свою модель прогнозирования для каждого уровня детализации сигнала. В качестве такой модели была выбрана нечеткая математическая модель на основе алгоритма Такаги-Сугено, параметры которой настраиваются при помощи адаптивной нейронечеткой сети (ННС) ANFIS.
Обучение и прогнозирование осуществляется для каждого уровня разложения в отдельности, поэтому для каждой из полученных временных последовательностей происходит независимое формирование входных векторов для ННС. Дополнительно на вход ННС поступает информация о номере часа, для которого осуществляется прогнозирование.
Так для низкочастотной составляющей, которая после вейвлет-фильтрации описывается аппроксимирующей с3(t) компонентой исходного ВР выделяется три участка в типовом суточном графике потребления – возрастание нагрузки (с 1 до 8 часов), относительное постоянство (с 9 до 16 часов) и убывание нагрузки (с 17 до 24 часов) (см. рис. 4). Каждый такой период кодируется определенной цифрой.
Такой подход позволяет учесть значимый фактор – номер часа, для которого строится прогноз и, в то же время, в результате обобщения по преобладанию выделить лишь три значения для дополнительного входа ННС, не перегружая ее большим количеством информации. При этом повышается точность прогнозирования.
Аналогичным образом для среднечастотной составляющей w3 более четко отражающей внутрисуточные колебания нагрузки – утренний и вечерний пик – в типовом суточном графике потребления выделяется четыре периода: с 3 до 8 часов и с 14 до 15; с 9 до 13 часов, и с 16 до 2 часов ночи. Для высокочастотных составляющих ВР электрической нагрузки, которые относятся к случайной компоненте, вход, отвечающий за номер часа, для которого строится прогноз, имеет 10 значений.
Глубина исторической выборки, подаваемой на вход, определяется эмпирически. Она также может быть приближенно оценена исходя из анализа автокорреляционной функции.
Также для каждой нечеткой математической модели необходимо задать число и вид функций принадлежности по каждому входу, а также создать базу нечетких правил. Эта процедура может быть автоматизирована. Так, математический пакет MatLab позволяет автоматически генерировать ANFIS-структуру из исходных данных.
Тестирование ННС осуществляется путем сравнения спрогнозированных значений нагрузки с фактическими за четверо суток и усреднением результатов расчета точности. Оценка адекватности построенной модели производится по следующему критерию:
MAPE – средняя ошибка в процентах:
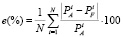 ,
,
где PA – фактическое значение нагрузки, PF – результат восстановления (прогноза) и N – количество данных (часов).
Если качество прогноза выполненного на построенной нейронечеткой модели является неудовлетворительным, указанные этапы построения системы прогнозирования электропотребления повторяются до тех пор, пока прогноз не будет соответствовать заданному критерию качества.
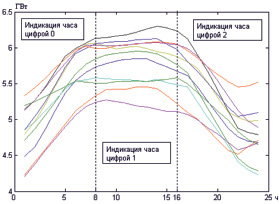
Рис. 4. Низкочастотная составляющая, которая после вейвлет-фильтрации описывается аппроксимирующей с3(t) компонентой исходного временного ряда
Допустимая относительная погрешность зависит от мощности потребления и интервала упреждения. Для ЭЭС средней мощности (5–8 ГВт) эта величина лежит в пределах 2–5 % [1].
Работа выполнена при финансовой поддержке гранта Президента Российской Федерации № 14.Z56.14.3734-МК.
Библиографическая ссылка
Филатова Е.С., Филатов Д.М., Стоцкая А.Д. МЕТОДИКА ПОСТРОЕНИЯ СИСТЕМЫ ПРОГНОЗИРОВАНИЯ ЭЛЕКТРОПОТРЕБЛЕНИЯ НА БАЗЕ НЕЙРОНЕЧЕТКОГО ПОДХОДА И ВЕЙВЛЕТ-ТЕОРИИ // Международный журнал прикладных и фундаментальных исследований. 2014. № 11-1. С. 26-29;URL: https://applied-research.ru/ru/article/view?id=6067 (дата обращения: 07.01.2026).

