Модернизация систем ориентации космических аппаратов (КА) напрямую связана с улучшением их эксплуатационных характеристик, уменьшением габаритов и материалоемкости, обеспечением прочности и долговечности. Стремление облегчить конструкцию и максимально использовать прочностные ресурсы материалов приводит к повышению уровня напряжения, что сопровождается увеличением деформаций.
Исполнительным органом активной пространственной системы ориентации космического аппарата является двигатель-маховик (ДМ). Основным рабочим органом ДМ является маховик с явно выраженным ободом 1, установленный в опорах 2 и приводимый во вращение электродвигателем 3, ротор которого закреплен на маховике, а статор – на основании 4 (рис. 1) [5].
Для минимизации уровня вибрации и возмущающих моментов, возникающих при работе ДМ в диапазоне угловой скорости вращения от 0 до 6000 об/мин необходимо на этапе проектирования проводить оценку напряженного состояния конструкции маховика под действием приложенных к системе постоянных во времени сил и определять собственные (резонансные) частоты.
Инновационное развитие многофункциональных компьютерных систем, согласованно выполняющих объемное конструирование и инженерные расчеты, позволяет осуществлять решение обозначенных прикладных задач механики.
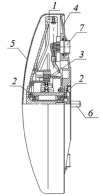
Рис. 1. Конструкция ДМ
В связи с активным внедрением в инженерную практику вычислительной техники, наиболее эффективным приближенным методом решения прикладных задач механики является метод конечных элементов, реализованный во многих программных средствах.
Метод конечных элементов (МКЭ) является сеточным методом, предназначенным для решения задач микроуровня, для которого модель объекта задается системой дифференциальных уравнений в частных производных с заданными краевыми условиями. С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя метод конечных элементов [1].
Формирование 3D-модели возможно с применением многих программных средств, в частности с использованием системы инженерного анализа T-FLEX CAD.
С использованием специализированной среды конечно-элементных расчетов T-FLEX Анализ возможно на этапе проектирования провести следующие виды анализов:
Частотный анализ позволяет осуществлять расчет собственных (резонансных) частот конструкции и соответствующих форм колебаний. Осуществляя проверку наличия резонансных частот в рабочем частотном диапазоне изделия и оптимизируя конструкцию таким образом, чтобы исключить возникновение резонансов, возможно повысить надежность и работоспособность изделия;
Статический анализ позволяет осуществлять расчет напряженного состояния конструкций под действием приложенных к системе постоянных во времени сил. С помощью данного модуля возможно оценить прочность разработанной конструкции по допускаемым напряжениям, определить наиболее слабые места и внести необходимые изменения (оптимизировать) [7].
3D-модель маховика сформирована в системе T-FLEX CAD в соответствии с рабочим чертежом детали.
Маховик имеет консольное исполнение с явно выраженным ободом для получения требуемого момента инерции. Материал маховика – хромированная нержавеющая сталь. Диаметр маховика – 350 мм, масса – 5,5 кг. На рис. 2 указано место частичного закрепления маховика необходимое для проведения инженерного анализа, обусловленное установкой радиально-упорных подшипников качения [4].
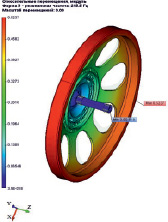
Оценить работоспособность маховика возможно при выполнении расчета его вибрационных характеристик, для чего необходимо определить собственные частота колебаний расчетным методом с использование системы T-FLEX Анализ. В результате частотного анализа получен ряд собственных частот 3D-модели маховика ДМ: 145,9 Гц, 215,5 Гц, 471,7 Гц, 604,9 Гц, 1389,8 Гц и т.д.
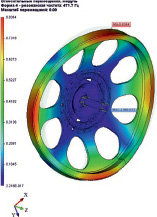
Формы мод колебаний маховика различаются на колебания без узловых линий – «зонтичные» (рис. 2, а), при которых неподвижной областью диска является его центральная часть и колебания с узловыми диаметрами – «веерные». «Веерные» колебания могут быть с двумя, тремя, четырьмя, пятью и шестью узловыми диаметрами (рис. 2, б, в, г). Например, при колебании диска с двумя узловыми диаметрами деформация его вдоль любой окружности представляет собой цепь из двух волн, причем колебания поверхности диска в секторах между узловыми диаметрами отличаются по знаку [3].
Достижение оптимального варианта конструкции в части удовлетворения массогабаритных и частотных требований возможно за счет использования параметрической модели маховика.
Основными нагрузками, действующими на маховик, являются центробежные силы, возникающие при вращении [6]. Определение напряжений и деформаций от центробежных сил – главный этап расчета на прочность.
Исследовать вибрационную надёжность маховика возможно путем расчетов, выполненных посредством статического анализа. Одной из важных опций статического анализа в среде T-FLEX Анализ для оценки жесткости проектируемой модели маховика является выбор в качестве приложения к модели такого нагружения как «вращение». «Вращение» позволяет приложить к системе центробежные и касательные силы инерции, возникающие при равномерном или ускоренном вращательном движении модели.
При задании условий «вращения» указывается ось вращения модели маховика и величина его угловой скорости (6000 об/мин).
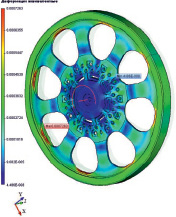
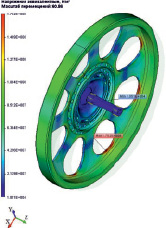
Обоснованные выводы о напряженном поведении конструкции и её прочности возможно посредством важнейшего инструментария системы конечно-элементного моделирования – постпроцессора, позволяющего проанализировать результаты расчетов. На рис. 3 приведены результаты статического анализа: деформации эквивалентные (а), коэффициент запаса по эквивалентным напряжениям (б), напряжения эквивалентные (в), модуль перемещения (г).
При рассмотрении проекции модели маховика по меткам экстремумов видно, что при максимальной угловой скорости маховика изменяются геометрические размеры за счет смещения центра масс и увеличения диаметра обода.
 а
а 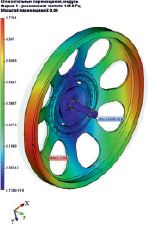 б
б
 в
в 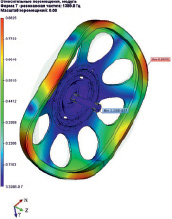 г
г
Рис. 2. Формы мод колебаний маховика: а – «зонтичные», б, в, г – «веерные»
Полученные результаты необходимо учитывать при отработке технологического процесса балансировки маховика на этапе изготовления (тип ротора, плоскости коррекции, их взаимовлияние), а также при проектировании подшипникового узла и выбора подшипников (перераспределение нагрузки при увеличении угловой скорости).
Использование системы T-Flex для создания и анализа параметрической трехмерной модели маховика позволяет легко и быстро менять его конструкцию, оценивать масс-инерционные и прочностные характеристики.
На этапе отработки конструкции эффективным инструментом инженерных решений, повышающих качество разработки и изготовления электромеханических изделий, является анализ динамических прочностных характеристик, полученных экспериментальным путем [2].
Модуль относительного перемещения характеризует максимальную амплитуду (размах) колебания полотна маховика при колебаниях в зависимости от числа узловых диаметров.
Оптимальность представленного варианта конструкции маховика (в рамках установленных требований по массогабаритных характеристикам) подтверждается значением первой собственной частоты, полученной посредством частотного анализа в системе T-FLEX CAD. Первая собственная частота 3D-модели маховика (145,9 Гц) по значению выше максимально возможной рабочей угловой скорости вращения ДМ (100 Гц).
Один из методов такого анализа на этапах предварительных испытаний – экспериментальный модальный анализ (ЭМА), позволяющий определить «слабые места» конструкции.
Общее представление о динамических характеристиках конструкции дает модальная (собственная) частота, демпфирование и форма моды, называемые модальными параметрами.
 а
а 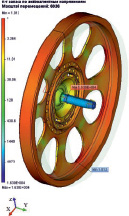 б
б
 в
в 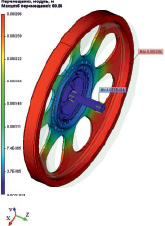 г
г
Рис. 3. Результаты статического анализа модели маховика ДМ: а – деформации эквивалентные, б – коэффициент запаса по эквивалентным напряжениям, в – напряжения эквивалентные, г – модуль перемещения
ЭМА основан на вычислении функции частотного отклика (FRF). Матрицы FRF определяются как отношение спектров Фурье реакции к спектрам Фурье силы, вызывающей реакцию:
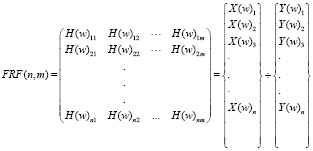
где: m – количество возбудителей; n – количество реакций; H(w) – FRF; X(w) – спектры Фурье выходных сигналов или реакций; Y(w) – спектры Фурье входных сигналов или сил возбуждения.
Сила возбуждения, как правило, измеряется динамометрическим датчиком. Перемещение при реакции измеряется датчиками ускорения, скорости или перемещения.
Приложение силы к испытываемой конструкции может осуществляться модальным молотком со встроенным датчиком силы или модальным вибратором.
Наиболее распространенным методом, используемым при анализе мод колебаний, является ударное возбуждение модальным молотком. Колебания, создаваемые при ударе, представляют собой переходный, кратковременный процесс передачи энергии. Спектр ударной силы является непрерывным, с максимальной амплитудой в зоне около 0 Гц и с последующим ее уменьшением с ростом частоты.
При анализе измерения отношения реакции к замеряемой силе возбуждения используется многоканальный анализатор, выполняющий быстрое преобразование Фурье. Определяемые частотные характеристики способствуют выделению спектров силы из результатов и описанию свойств конструкции между точками замера. По набору замеренных в различных точках конструкции частотных характеристик можно построить картину ее динамического поведения.
Стенд для проведения ЭМА состоит из стойки с двухкаскадной системой амортизации и пружинной подвески (предназначенной для подвешивания объекта исследования) с собственной нижней резонансной частотой не выше 3 Гц, многоканального анализатора, соединительных кабелей, персонального компьютера, виброизмерительных преобразователей.
Непосредственным результатом модальных испытаний являются представленные в виде изображений формы мод и связанные с ними резонансы и коэффициенты демпфирования.
На рис. 4 представлен подвешенный маховик с установленными на нем посредством мастики виброизмерительными преобразователями. В данном случае ударное воздействие осуществлялось модальным молотком по длине окружности обода маховика. Результаты представлены в табл. 1.
Таблица 1
Результаты ЭМА маховика при ударном воздействии модальным молотком
|
Мода колебания |
Частота, Гц |
Демпфирование, % |
|
1 |
360 |
0,3 |
|
2 |
834 |
1,1 |
|
3 |
861 |
0,9 |
Для оценки динамического состояния маховика под действием центробежных сил, возникающих при его вращении, необходимо прикладывать силу непосредственно в центр маховика (по оси вращения).
В случае использования модального вибратора воздействие осуществляется через стингер, установленный на динамометрическом датчике, контролируемом уровень создаваемого воздействия (рис. 5).
Полученные результаты показывают, что в целом конструкция маховика является достаточно жесткой с некритичным уровнем коэффициентов демпфирования на выявленных собственных частотах.


Рис. 4. ЭМА маховика при ударном воздействии модальным молотком

Рис.5. ЭМА маховика при ударном воздействии модальным вибратором
Таблица 2
Результаты ЭМА маховика при ударном воздействии модальным вибратором
|
Мода колебания |
Частота, Гц |
Демпфирование, % |
|
1 |
171 |
0,9 |
|
2 |
360 |
0,4 |
|
3 |
367 |
0,3 |
|
4 |
622 |
0,4 |
|
5 |
757 |
0,8 |
|
6 |
848 |
1,1 |
Значение первой собственной частоты маховика больше значения максимальной угловой скорости вращения ДМ, что позволяет исключить возникновение резонанса, вызванного собственной конструкционной частотой, в рабочем режиме ДМ.
Формы мод колебаний маховика представляются в виде анимации точек конструкции, перемещение которых моделируется посредством специализированного программного обеспечения.
Использование представленных методов оценки прочностных характеристик позволяет обеспечивать оптимальный комплекс эксплуатационных параметров маховика, который является одним из основных конструктивных элементов электромеханического исполнительного органа системы ориентации КА.
Библиографическая ссылка
Бритова Ю.А., Дмитриев В.С., Костюченко Т.Г. ПРОЧНОСТНОЙ АНАЛИЗ КОНСТРУКЦИИ МАХОВИКА ДВИГАТЕЛЯ СИСТЕМЫ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА НА ЭТАПЕ ПРОЕКТИРОВАНИЯ И ОТРАБОТКИ // Международный журнал прикладных и фундаментальных исследований. 2014. № 11-4. С. 541-546;URL: https://applied-research.ru/ru/article/view?id=6175 (дата обращения: 03.03.2026).

