Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ищукова Е.А. 1

---

1 Южный Федеральный Университет Институт компьютерных технологий и информационной безопасности

В статье рассматриваются основные этапы оценки стойкости современных блочных шифров с использованием метода линейного криптоанализа. Показана возможность применения распределенных многопроцессорных вычислений для сокращения времени анализа и повышения эффективности алгоритма. Приведен обзор известных фактов об анализе различных блочных шифров с использованием метода линейного криптоанализа.

Статья в формате PDF

940 KB

Линейный криптоанализ

секретный ключ

эффективность

отклонение

распределенные многопроцессорные вычисления

1. Бабенко Л.К., Ищукова Е.А. Анализ алгоритма ГОСТ 28147-89: поиск слабых блоков // Известия ЮФУ. Технические науки. Тематический выпуск «Информационная безопасность». – Таганрог: Изд-во ТТИ ЮФУ. – 2014. – № 2(151) – С. 148–157.

2. Бабенко Л.К., Ищукова Е.А. Использование слабых блоков замены для линейного криптоанализа блочных шифров // Известия ЮФУ. Технические науки. Тематический выпуск «Информационная безопасность». – Таганрог: Изд-во ТТИ ЮФУ. – 2014. – № 2(151). – С. 136–147.

3. Бабенко Л.К., Ищукова Е.А. Современные алгоритмы блочного шифрования и методы их анализа – М.: Гелиос АРВ. – 2006. – 376 с.

4. Шнайер Б. Прикладная криптография: Протоколы, алгоритмы, исходные тексты на языке Си – М.: Триумф. – 2002. – 648 с.

5. Matsui M. Linear Cryptanalysis Method for DES Cipher // Advances in Cryptology – Eurocrypt’93. – Springer-Verlag, 1998. – p. 386.

Долгое время криптография оставалась секретной наукой, в тайны которой был посвящен лишь узкий круг лиц. Это было естественно. Так как в первую очередь она была направлена на сохранение государственных секретов. Ситуация стала меняться во второй половине ХХ века с появлением персональных компьютеров. Когда практически каждый человек получил возможность оперировать электронной информацией, возникла естественная потребность как-то защищать эту информацию от посторонних глаз. На сегодняшний день наука криптография развивается очень стремительно. Связано это с тем, что в последние годы данная область знаний стала открытой. Если раньше созданием и анализом шифров занимались лишь секретные государственные структуры, то в наши дни любой желающий может беспрепятственно овладеть азами данной науки. Кроме того, быстрое развитие современных информационных технологий также делает криптографию востребованной. Как следствие появляются все новые и новые шифры, предлагаемые авторами разных стран, направленные на усиление секретности данных, шифруемых с их помощью.

Широкое распространение получило использование симметричной криптографии, а несколько позднее и ассиметричной. В 1976 году в США был утвержден стандарт шифрования данных DES (Data Encryption Standard), который использовался довольно длительное время (более 20 лет). Естественно, что у людей возникло желание проверить: а действительно ли предлагаемые алгоритмы для шифрования конфиденциальных данных обеспечивают сохранность информации? Для того, чтобы ответить на этот вопрос необходимо было провести ряд достаточно сложных исследований. Так, исследования в области анализа стойкости шифров постепенно стали причиной того, что в криптологии выделилось два родственных направления, теснейшим образом связанных между собой: криптография и криптоанализ. Прослеживая историю развития этих направлений, можно сказать, что одним из блочных алгоритмов наиболее часто подвергавшийся различного рода атакам является алгоритм шифрования DES. Именно для анализа этого алгоритма шифрования были разработаны такие мощные атаки как линейный и дифференциальный криптоанализ, которые в дальнейшем стали применяться к целому классу блочных шифров. В настоящий момент, знание азов применения данных двух методов анализа, позволяет еще на этапе проектирования шифров заложить в них избыточную устойчивость и заведомо пресечь возможность применения данных методов анализа к вскрытию зашифрованной информации. В настоящей работе предлагается рассмотреть основные принципы, лежащие в основе метода линейного криптоанализа и оценить степень его эффективности.

1. Основные сведения о линейном криптоанализе

Метод линейного криптоанализа впервые был предложен в начале 90-х годов XX века японским ученым М. Матсуи (Matsui). В своей работе [5] М. Матсуи показал, как можно осуществить атаку на алгоритм шифрования DES, сократив сложность анализа до 247. Существенным недостатком метода стала необходимость иметь в наличии большой объем данных, зашифрованных на одном и том же секретном ключе, что делало метод малопригодным для практического применения к вскрытию шифра. Однако, если предположить, что к аналитику в руки попал шифрованный текст, содержащий важные сведения, а также некий черный ящик (устройство или программа), который позволяет выполнить любое число текстов, зашифрованных с помощью известного алгоритма шифрования на секретном ключе, не раскрывая при этом самого ключа, то применение метода линейного криптоанализа становится вполне реальным. Позднее М. Матсуи усовершенствовал свою атаку и показал, как можно понизить сложность анализа до 243. Для алгоритма DES метод линейного анализа остался скорее задачей гипотетической, ввиду того, что для анализа требуется огромный объем информации, зашифрованной на одном и том же секретном ключе. Перехватить такой объем информации в реальных условиях практически невозможно. Однако, некоторые алгоритмы шифрования, известные на момент опубликования работы [5], в последствии были проверены на устойчивость к этому методу. Не все из них оказались достаточно стойкими и, как следствие, потребовали доработки.

Знание механизмов работы метода линейного криптоанализа позволяет криптографам еще на этапе проектирования крптоалгоритмов обеспечить стойкость шифров. Вот почему так важно уметь применять известные методы криптоанализа на практике.

2. Определение линейного аналога и его эффективности

Итак, рассмотрим основные понятия, связанные с методом линейного криптоанализа. Любой алгоритм шифрования в самом общем виде можно представить как некоторую функцию E (от англ. Encryption – шифрование), зависящую от входного сообщения Х, секретного ключа К и возвращающую шифрованное сообщение Y:

Y = E(X, K). (1)

Зная само преобразование Е и входное сообщение Х, нельзя однозначно сказать каким будет выходное сообщение Y. В данном случае нелинейность функции (1) зависит от внутренних механизмов преобразования Е и секретного ключа К.М. Матсуи показал, что существует возможность представить функцию шифрования (1) в виде системы уравнений, которые выполняются с некоторой вероятностью р. При этом для успешного проведения анализа вероятность уравнений р должна быть как можно дальше удалена от значения 0,5 (то есть приближаться либо к 0 либо к единице). Так как уравнения, получаемые в ходе анализа криптоалгоритма, являются вероятностными, то их стали называть линейными статистическими аналогами.

Определение 1. Линейным статистическим аналогом нелинейной функции шифрования (1) является величина Q, равная сумме по модулю два скалярных произведений входного вектора Х, выходного вектора Y и вектора секретного ключа К соответственно с двоичными векторами a, β и g, имеющими хотя бы одну координату равную единице:

,

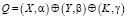в том случае, если вероятность того, что Q = 0 отлична от 0,5 (Р(Q = 0) ≠ 0,5).

Например, для полного 16-раундового алгоритма DES линейный статистический аналог будет иметь вид [3]:

PR[16,20] ⊕ PL[8,14,25] ⊕ CR[3,8,14,25] ⊕CR[1,2,4,5] ⊕ CL[17] = K1[29,25] ⊕ K3[26] ⊕ K4[4] ⊕ K5[26] ⊕ K7[26] ⊕ K8[4] ⊕ K9[26] ⊕ K11[26] ⊕ K12[4] ⊕ K13[26] ⊕K15[26] ⊕ K16[2,3,5,6],

где PR правая часть входного сообщения, PL – левая часть входного сообщения, СR правая часть выходного сообщения, СL – левая часть выходного сообщения, К – секретный ключ, индексы в квадратных скобках указывают на номера битов, которые участвуют в формировании линейного аналога.

В отличие от дифференциального криптоанализа, в котором большое значение вероятности гарантирует успех атаки, в линейном криптоанализе успех анализа может быть обеспечен как уравнениями с очень большой вероятностью, так и уравнениями с очень маленькой вероятностью. Для того, чтобы понять, какое из возможных уравнений лучше всего использовать для анализа используют понятие отклонения.

Определение 2. Отклонением линейного статистического аналога называют величину h = |1 – 2 р|, где р – вероятность, с которой выполняется линейный аналог.

Отклонение определяет эффективность линейного статистического аналога. Чем отклонение больше, тем выше вероятность успешного проведения анализа. Фактически отклонение показывает насколько вероятность статистического аналога отдалена от значения р = 0,5.

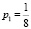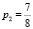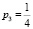Рассмотрим пример. Пусть имеется три линейных аналога, вероятности для которых соответственно равны , и . Определим какой из этих аналогов лучше всего использовать для анализа. Для этого найдем отклонения аналогов:

;

;

.

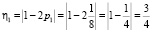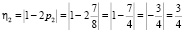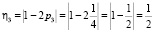Видно, что наибольшее отклонение имеют первый и второй аналоги при том, что значение вероятностей у них различны. Для того, чтобы лучше понять смысл значения отклонения обратимся к рис. 1 из которого наглядно видно, что аналоги с различными вероятностями отклоняются на одинаковое расстояние от точки р = 0,5.

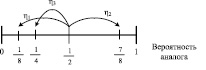
Отклонения линейных статистических аналогов

3. Основные этапы линейного криптоанализа

Для успешного применения метода линейного криптоанализа необходимо решить следующие задачи:

1. Найти максимально эффективные (или близкие к ним) статистические линейные аналоги. При нахождении аналогов обратить внимание на то, что в них должно быть задействовано как можно больше битов искомого секретного ключа К.

2. Получить статистические данные: необходимый объем пар текстов (открытый – закрытый текст), зашифрованных с помощью анализируемого алгоритма на одном и том же секретном ключе. При этом можно воспользоваться Парадоксом о Днях рождениях для определения минимального объема данных, необходимого для успешного анализа с вероятностью 0,5.

3. Определить ключ (или некоторые биты ключа) путем анализа статистических данных с помощью линейных аналогов.

Первый шаг анализа заключается в нахождении эффективных статистических аналогов. Для алгоритмов шифрования, в которых все блоки заранее известны, этот шаг можно выполнить единожды, основываясь на анализе линейных свойств всех криптографических элементов шифра. В результате анализа должна быть получена система уравнений, выполняющихся с некоторыми вероятностями. Левая часть уравнений должна содержать в себе сумму битов входного и выходного сообщения, правая часть уравнения – биты секретного ключа. Система уравнений должна быть определенной, то есть содержать все биты исходного секретного ключа. Данный этап не является вычислительно сложным, однако требует больших знаний, логики работы и внимательности. Он может быть автоматизирован. Однако при этом необходимо помнить, что для каждого определенного алгоритма шифрования система линейных аналогов строиться всего один раз и в дальнейшем может быть использована для нахождения разных секретных ключей шифрования, которые используются для шифрования данных с помощью анализируемого шифра. Исключение составляют те блочные шифры, в которых присутствуют нефиксированные элементы. Наглядным примером может служить алгоритм шифрования ГОСТ 28147-89, у которого блоки замены могут быть различны. Как следствие, первый шаг по нахождению статистических аналогов надо будет проделывать снова и снова для каждой новой конфигурации блоков замены.

Если первый шаг анализа является чисто теоретическим и полностью зависит от структуры алгоритма, то второй шаг – является исключительно практической частью, которая заключается в анализе известных пар открытый-закрытый текст с помощью полученной ранее системы статистических аналогов. Для этого используется следующий алгоритм.

Алгоритм. Пусть N – число всех открытых текстов и Т – число открытых текстов, для которых левая часть линейного статистического аналога равна 0. Рассмотрим два случая.

1. Если Т > N/2, то в этом случае число открытых текстов, для которых левая часть аналога равна нулю, больше половины, то есть в большинстве случаев в левой части аналога появляется значение, равное нулю, то

а) если вероятность этого линейного статистического аналога р > 1/2, это говорит о том что в большинстве случаев правая и левая части аналога равны, а значит левая часть аналога, содержащая биты ключа, равна 0 (К = 0, если р > 1/2).

б) если вероятность этого линейного статистического аналога р < 1/2, это говорит о том что в большинстве случаев правая и левая части аналога не равны, а значит левая часть аналога, содержащая биты ключа, равна 1 (К = 1, если р < 1/2).

2. Если Т < N/2, то в этом случае число открытых текстов, для которых левая часть аналога равна нулю, меньше половины, то есть в большинстве случаев в левой части а) аналога появляется значение, равное единице, то

если вероятность этого линейного статистического аналога р > 1/2, это говорит о том что в большинстве случаев правая и левая части аналога равны, а значит левая часть аналога, содержащая биты ключа, равна 1 (К = 1, если р > 1/2).

б) если вероятность этого линейного статистического аналога р < 1/2, это говорит о том что в большинстве случаев правая и левая части аналога не равны, а значит левая часть аналога, содержащая биты ключа, равна 0 (К = 0, если р < 1/2).

Успех алгоритма возрастает с ростом N и Δ = |1 – 2p|.

Данный алгоритм будет иметь успех при анализе большого числа текстов N. Следовательно, второй шаг анализа является вычислительно сложным. Поэтому для ускорения времени анализа можно и нужно использовать параллельные вычисления.

В результате работы вышеприведенного алгоритма будет получена определенная (а возможно и переопределенная) система уравнений, отражающая взаимосвязь битов ключа. Третий шаг анализа заключается в решении данной системы, например, методом Гаусса, что позволит получить значения битов секретного ключа шифрования.

Более подробно о линейном криптоанализе различных блочных алгоритмов шифрования можно почитать в работе [3].

4. Уязвимость различных шифров к методу линейного криптоанализа

Проведя обзор большого числа различных статей и обзоров, удалось собрать не так уж много информации о применимости метода линейного криптоанализа к современным блочным шифрам. Скорее всего это связано с тем, что в современные блочные шифры, появившиеся в последнее десятилетие, еще на этапе проектирования заложена устойчивость к методу линейного криптоанализа. Однако, никогда не стоит забывать о том, что если в настоящий момент нет сведений об успешном анализе того или иного шифра – это не значит, что анализ невозможен. Скорее всего, мы просто еще не придумали способ, как провести успешный анализ.

Итак, подведем итог и соберем вместе имеющуюся информацию. Считается, что метод линейного криптоанализа в неявном виде был предложен еще в работе Шона Мерфи в 1990 году, где он успешно применялся при анализе системы блочного шифрования FEAL.

В 2001 году Э. Бихам, Орр Данкелман и Н. Келлер предложили, как с помощью линейного криптоанализа провести анализ 10 из 32 раундов для алгоритма Serpent-128. Для этого им потребовалось 2118 открытых текстов. Позднее они усовершенствовали алгоритм и осуществили анализ 11 раундов шифра Serpent-192/256 с таким же количеством текстов. Однако общее время анализа при этом возрасло значительно (с 289 до 2187).

В продолжении работы над алгоритмом FEAL был предложен шифр FEAL-N (Miyaguchi, 1990), где «N» является параметром, выбираемым пользователем, и шифр FEAL-NX, который имеет более длинный 128-битный секретный ключ. Первоначально Тарди-Кордиф и Гилберт (Tardy-Corfdir and Gilbert, 1991), а позднее Матсуи и Ямагаши (Matsui and Yamagishi, 1992) показали нестойкость данных шифров к методу линейного криптоанализа. Позже было показано, что FEAL-4 можно вскрыть при наличии всего 5 открытых текстов, FEAL-6 – при наличии 100, и FEAL-8 – при наличии 215 текстов. В 1994, Ота и Аоки (Ohta and Aoki) предложили линейный криптоанализ для алгоритма FEAL-8, который требовал всего 212 известных открытых текстов.

На первый взгляд шифр Madryga выглядит менее стойким по сравнению с алгоритмом DES. В алгоритма Madryga все операции линейны, в отличие от алгоритма DES, в котором S-блоки обладают свойством нелинейности. Однако, используемые в алгоритме Madryga сдвиги и дата-зависимые операции, позволяют противостоять линейному криптоанализу.

Также было показано, что с помощью линенйного криптоанализа можно произвести анализ алгоритма шифрования NUSH быстрее, чем с помощью метода полного перебора.

Показано, что шифр Q уязвим с помощью метода линейного криптоанализа. Келихер, Мейер и Таварес (Keliher, Meijer, and Tavares) провели успешную атаку с вероятностью 98,4 %, используя 2⁹⁷ известных открытых текстов.

Считается, что не известно результатов о полном анализе алгоритма шифрования SC2000, однако версия, в которой 4,5 раунда, является уязвимой к методу линейного криптоанализа.

Группой ученых (Taehyun Kim, Jongsung Kim, Seokhie Hong and Jaechul Sung) показано, что существует возможность применить метод линейного криптоанализа к 22-раундовому алгоритму шифрования SMS4. При этом потребуется 2¹¹⁷ известных открытых текстов, 2¹⁰⁹ байтов памяти и временная сложность составит 2^109.86, при этом будет выполнено 2^120.39 арифметических операций.

До сих пор остается открытым вопрос насколько заполнение S-блоков влияет на стойкость алгоритма ГОСТ, хотя считается, что большого количества раундов и избыточной длины ключа достаточно для обеспечения его стойкости. В книге Б. Шнайера [4] говорится о том, что за счет большого числа раундов шифрования линейный криптоанализ практически не применим к полнораундовому алгоритму ГОСТ. На сегодняшний день нет достаточно подробных исследований стойкости алгоритма шифрования ГОСТ к методу линенйого криптоанализа. Однако в работах [1, 2] рассмотрена возможность поиска сильных и слабых блоков для алгоритма ГОСТ, а также их использования для дальнейшего анализа.

Библиографическая ссылка