Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Назарова М.В. 1 Фефелова Т.Л. 1

---

1 Камышинский технологический институт (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет»

В статье приведены результаты выполнения исследовательской работы по разработке оптимальных технологических параметров выработки ткани полотняного переплетения на ткацком станке СТБ-2-216 с заданной жесткостью. В ходе выполнения работы проведен активный эксперимент по определению параметров работы ткацкого станка СТБ-2-216, при которых жесткость ткани будет максимальной. При выполнении эксперимента изменялись следующие параметры ткацкого станка: натяжение нитей основы, плотность ткани по утку, угол поворота главного вала станка в момент заступа. В ходе выполнения работы получены математические модели, описывающие влияние параметров работы ткацкого станка на жесткость ткани. При оптимизации технологического процесса выработки ткани полотняного переплетения был использован метод канонического преобразования математической модели. Анализ полученных сечений поверхностей отклика позволил определить оптимальные технологические параметры работы бесчелночного ткацкого станка СТБ-2-216 при выработке ткани с максимальной жесткостью по основе и с максимальной жесткостью по утку.

Статья в формате PDF

1489 KB

жесткость ткани

ткацкой станок

математическая модель

оптимизация

1. Букаев П.Т. Разработка параметров оптимального процесса бесчелночного ткачества и критериев его оценки. ЛИТЛП. – Дисс. ... канд. техн. наук – Л.: 1984 – 402 с.

2. Букаев П.Т. Разработка теxнологическиx основ бесчелночного ткачества. Автореферат дисс. ... докт.теxн.наук. – М.: ЦНИXБИ, 1985. – 45 с.

3. Исследование влияния вида уточных нитей на сминаемость ткани бельевой группы / С.Ю. Земцова, М.В. Назарова // России – творческую молодежь: материалы I Всероссийской научно-практической студенческой конференции, г. Камышин, 22–23 мая 2013 г. В 4 т. Т.1 / ФГБОУ ВПО ВолгГТУ КТИ (филиал) ВолгГТУ. – Волгоград, 2013. – С. 122–125.

4. Исследование влияния различного вида переплетения ткани на ее прочностные и гигиенические свойства / В.Ю. Романов, Н. Фомина // Инновационные технологии в обучении и производстве: Материалы VI Всероссийской научно-практической конференции г. Камышин 15-16 декабря 2009 г.: Т.2 / Федеральное агентство по образованию, Государственное образовательное учреждение высшего профессионального образования «Волгоградский Государственный технический университет», Камышинский технологический институт (филиал) ГОУ ВПО «Волгоградский Государственный технический университет». – Волгоград, 2010. – С. 147–149.

5. Исследование зависимости несминаемости бельевых тканей от заправочных параметров ткацкого станка / Е.К. Ермилова, С.Ю. Бойко // Нижнему Поволжью – творческую молодёжь: матер. VI регион. науч.-практ. студ. конф., посв. 200-летию победы России в Отечественной войне 1812 г., г. Камышин, 17–18 мая 2012 г. В 6 т. Т.2 / ФГБОУ ВПО ВолгГТУ КТИ (филиал) ВолгГТУ . – Камышин, 2012. – С. 21–23.

6. Исследование зависимости сминаемости ткани полотняного переплетения от вида уточных нитей / М.А. Сухова, В.Ю. Романов // Нижнему Поволжью – творческую молодёжь: матер. VI регион. науч.-практ. студ. конф., посв. 200-летию победы России в Отечественной войне 1812 г., г. Камышин, 17–18 мая 2012 г. В 6 т. Т.2 / ФГБОУ ВПО ВолгГТУ КТИ (филиал) ВолгГТУ. – Камышин, 2012. – С. 60–62.

7. Исследование напряженно-деформированного состояния нитей основы по ширине заправки ткацкого станка типа СТБ / В.Г Шляхтина, С.Ю. Бойко // Нижнему Поволжью – творческую молодёжь: матер. VI регион. науч.-практ. студ. конф., посв. 200-летию победы России в Отечественной войне 1812 г., г. Камышин, 17–18 мая 2012 г. В 6 т. Т.2 / ФГБОУ ВПО ВолгГТУ КТИ (филиал) ВолгГТУ . – Камышин, 2012. – С. 65–67.

8. Свид. о гос. регистрации программы 2013615531 РФ, Оптимизация технологических процессов ткацкого производства по данным активного эксперимента, проведенного по матрице планирования Бокс-3 / М.В. Назарова, В.Ю. Романов. – № 2013613426; заявлено 23.04.2013; опубликовано 13.06.2013.

Одной из наиболее важных и актуальных проблем в текстильной промышленности является повышение качества и улучшение существующего ассортимента продукции. При оценке качества материалов, предназначенных для изго­товления верхней одежды, в основном костюмно-плательных тка­ней различного волокнистого состава обычно используют показатель жесткости ткани.

Жесткость характеризует способность материала сопротив­ляться изменению формы (размеров) под действием различно прилагаемых сил и деформаций, например растяжения, круче­ния, изгиба, смятия и других.

Являясь характеристикой, которая может определять целе­вое назначение материала, жесткость тканей оказывает влия­ние на поведение тканей при переработке (изготовлении швей­ных изделий) и в эксплуатации. Например, прикладные и про­кладочные ткани должны обладать достаточной жесткостью, обеспечивающей неизменность формы деталей одежды. Подкла­дочные ткани, наоборот, должны быть мягкими, податливыми, чтобы они не влияли на изменение формы верхних материалов.

Для тканей обычно определяют жесткость при изгибе, так как этот вид деформации наиболее часто встречается в готовых изделиях.

Жесткость и несминаемость тканей зависят от механических и геометрических характеристик свойств составляющих их во­локон, структуры пряжи и ткани.

Тонкие и более длинные волокна обладают меньшей жест­костью. Они меньше деформируются и имеют большее сцеп­ление одно с другим; это препятствует их смещению в пряже при смятии ткани. Естественно, ткани из таких волокон более несминаемы, чем ткани из грубых и коротких волокон.

Что касается переплетений, наиболее «жестким и сминае­мым» переплетением является полотняное (по сравнению с сар­жевым и атласным).

Таким образом, жесткость ткани является одним из основных показателей, характеризующих внешний вид ткани. Поэтому в данной работе решалась актуальная задача выбора таких технологических параметров ткацкого станка, при которых будет обеспечиваться заданная жесткость ткани. Для этого в лаборатории ткачества Камышинского технологического института при выработке ткани полотняного переплетения на бесчелночном ткацком станке СТБ-2-216 был проведен эксперимент, целью которого являлся подбор таких параметров заправки станка, при которых жесткость ткани будет максимальной. В качестве выходных параметров эксперимента принимаем:

У1 – жесткость ткани по основе, мм

У2 – жесткость ткани по утку, мм.

При выборе ткани для исследования исходим из следующих соображений:

– в тканях полотняного переплетения (при всех прочих равных условиях) нити наиболее связаны между собой, в них в большей степени может быть использована прочность нитей;

– короткие основные и уточные перекрытия позволяют говорить о лучшей устойчивости к механическим воздействиям;

– в последнее время ткани полотняного переплетения получили широкое распространение, так как позволяют значительно уменьшить массу квадратного метра ткани по сравнению с тканями других переплетений.

Характеристика исследуемой ткани представлена в табл. 1.

Таблица 1

Характеристика ткани, взятой для исследования

Методом проведения эксперимента для получения математической модели, описывающей влияние заправочных параметров ткацкого станка СТБ-2-216 на жесткость ткани, выбран активный эксперимент с использованием матрицы планирования Бокс-3. Выбор метода Бокса обусловлен тем, что этот метод позволяет получать статические математические модели процессов, используя факторное планирование, регрессионный анализ и движение по градиенту. При этом предполагается, что множество определяющих факторов задано. Каждый из факторов управляем, результаты опытов воспроизводятся, опыты равноценны, решается задача поиска оптимальных условий, математическая модель процесса заранее неизвестна.

Из опыта проведенных ранее исследований известно, что наибольшее влияние на жесткость ткани оказывают следующие параметры заправки и выработки ткани:

– натяжение нитей основы, сH – Х1;

– плотность ткани по утку, нит/дм – X2;

– угол поворота главного вала станка в момент заступа, град – X3.

Опираясь на данные предварительного эксперимента, были определены значения интервалов варьирования и основных уровней варьирования факторов. Эти данные представлены в табл. 2.

По матрице планирования Бокс-3 был проведен эксперимент на станке СТБ-2-216 при выработке ткани полотняного переплетения. Ткань, полученная в результате эксперимента, была подвергнута испытаниям на жесткость по стандартной методике на гибкомере ПТ-2 (рис. 1). В ходе эксперимента испытывались пять основных и пять уточных полосок размером 160х30 мм.

Таблица 2

Уровни и интервалы варьирования факторов эксперимента

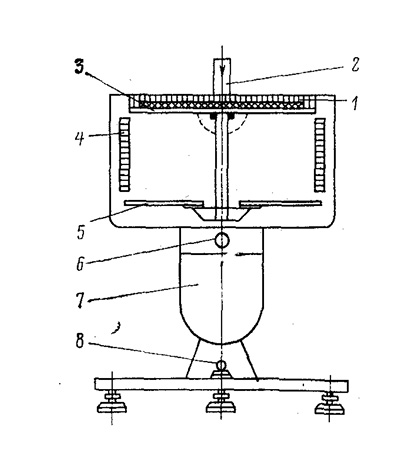
Рис. 1. Схема гибкомера ПТ-2 для определения жесткости полотен при изгибе: 1 – пробная полоска; 2 – груз; 3 – горизонтальная опорная площадка; 4 – шкала; 5 – указатель прогиба; 6 – винт; 7 – механизм опускания боковых полочек опорной площадки; 8 – тумблер

Жесткость такни EI (мкН×см2) вычисляют отдельно для образцов ткани по направлению основы и по направлению утка по формуле:

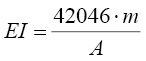; (1)

где m – масса пробных образцов ткани, определенная с точностью до 0,01 г;

А – коэффициент, определяемый как функция относительного прогиба.

Относительный прогиб ткани определяется по формуле:

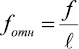; (2)

где f – средний прогиб образцов ткани по основе и утку, с точностью до 0,001;

ℓ – длина свешивающейся части пробного образца ткани, равного 70 мм.

Коэффициент жесткости определяют как отношение жесткости ткани в продольном направлении к жесткости ткани в поперечном направлении:

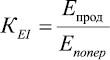(3)

Экспериментальные данные испытаний ткани полотняного переплетения на жесткость представлены в табл. 3 и 4.

Обработка результатов эксперимента проводилась с использованием ЭВМ в среде программирования MathCad отдельно для каждого выходного параметра.

Таблица 3

Жесткость ткани полотняного переплетения по направлению основы

Таблица 4

Жесткость ткани полотняного переплетения по направлению утка

Получены следующие математические модели зависимости жесткости ткани по направлениям основы и утка в зависимости от заправочных параметров ткацкого станка СТБ-2-216:

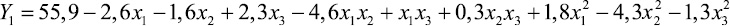(4)

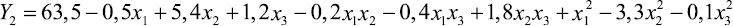(5)

Анализ математической модели (4) позволяет сделать вывод о том, что наибольшее влияние на жесткость ткани по направлению основы оказывает величина заправочного натяжения, причем, при увеличении заправочного натяжения, жесткость ткани по основе уменьшается. Наименьший вклад на жесткость ткани по основе оказывает величина плотности ткани по утку.

Анализ математической модели (5) позволяет сделать вывод о том, что наибольшее влияние на жесткость ткани по утку оказывает величина плотности ткани по утку, причем, при увеличении плотности ткани по утку, жесткость ткани по утку увеличивается. Наименьший вклад на жесткость ткани по утку оказывает величина заправочного натяжения.

Для выполнения задачи разработки оптимальных технологических параметров заправки и выработки ткани полотняного переплетения на ткацком станке СТБ-2-216 в качестве метода оптимизации технологического процесса был выбран метод канонического преобразования математической модели. В соответствии с алгоритмом выбранного метода оптимизации была разработана математическая модель задачи оптимизации технологического процесса выработки ткани полотняного переплетения, которая выглядит следующим образом:

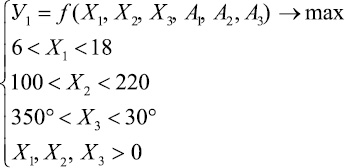
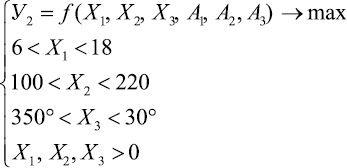(6)

При построении сечений поверхностей отклика при числе факторов n = 3 один из факторов фиксируется на нулевом уровне.

Построение двухмерных сечений поверхностей отклика выходного параметра оптимизации процесса выработки ткани полотняного переплетения осуществлялось на ЭВМ, в среде программирования MathCad отдельно для каждого выходного параметра. Полученные сечения представлены на рис. 2 и 3.

Анализ сечения поверхности отклика математической модели зависимости жесткости ткани по основе позволил сделать следующий вывод: при фиксированном значении х1 (заправочное натяжение нитей основы) экстремум целевой функции достигается при х2 (плотность ткани по утку) в интервале от –0,25 до –0,15 (в кодированных значениях), или 145 нит/см до 150 нит/см (в натуральных значениях), а также при х3 – угол заступа, в интервале от + 0,75 до + 1,0 (в кодированных значениях), от 25 град до 30 град (в натуральных значениях).

Анализ сечения поверхности отклика математической модели зависимости жесткости ткани по утку позволил сделать следующий вывод: при фиксированном значении х1 = 0 экстремум целевой функции достигается при х2 = 1 и х3 = 1 (в кодированных значениях).

Выводы

1. Для выработки ткани полотняного переплетения с максимальной жесткостью по основе на ткацком станке СТБ-2-216 необходимо установить следующие параметры:

– натяжение нитей основы – 12 у.е.;

– плотность ткани по утку 145…150 нит/дм;

– угол поворота главного вала станка в момент заступа 25…30 град.

2. Для выработки ткани полотняного переплетения с максимальной жесткостью по утку на ткацком станке СТБ-2-216 необходимо установить следующие параметры:

1. натяжение нитей основы – 12 у.е.;

2. плотность ткани по утку 220 нит/дм;

3. угол поворота главного вала станка в момент заступа 350 град.

Библиографическая ссылка