При обработке деталей поверхностным пластическим деформированием между роликом и деталью возникает проскальзывание, приводящее к возникновению трения на контактной поверхности. В свою очередь трение между роликом и деталью является одним из факторов существенно изменяющим качество поверхностного слоя. Одной из причин, вызывающих проскальзывание является несовпадение направления осей ролика и детали.
Для решения задачи об определении этого проскальзывания поверхности ролика относительно поверхности детали составим разность векторов скоростей точек поверхности контактной зоны, принадлежащей детали, и соприкасающихся с ним точек поверхности ролика.
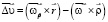, (1)
где ωp, ωд – угловые скорости ролика и детали; r – радиус ролика в данном сечении, перпендикулярном оси ролика; ρ – радиус-вектор точки поверхности контактной зоны проведенной от оси детали.
Пятно контакта относительно системы координат, в которой ось OX совпадает с осью детали, ось OZ расположена в плоскости, относительно которой производится отсчет угла самозатягивания a и ось OY перпендикулярна указанным осям, изображено на рис. 1.
Рис. 1. Схема контактной зоны для определения проскальзывания ролика
Представляя правую часть равенства (1) в виде суммы определителей и раскладывая эти определители по элементам первой строки, найдем составляющие вектора проскальзывания по координатным осям:
;
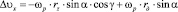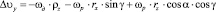; (2)
;
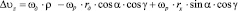где составляющие радиус-векторов точек поверхности контакта и радиусов точек поверхности ролика по координатным осям равны
;
;
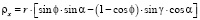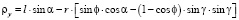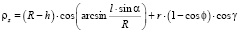; (3)
;
;
;
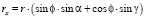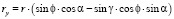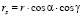где R – радиус обрабатываемой детали, h – изменение глубины внедрения ролика по длине контакта, φ – угол между радиусом ролика и линией, проведенной через ось ролика и середину ширины контакта; γ – угол внедрения.
Рассмотрим зависимость изменения скорости проскальзывания ролика от угла самозатягивания α.
Полагая в формулах (2) φ = γ = 0, α ≠ 0, т.е. условия, определяющие максимальную деформацию точек обрабатываемой поверхности, получим:
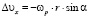; (4)
;
,
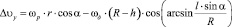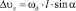полагая α = 0, будем иметь:
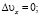
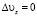(5)
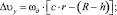
где отношение угловых скоростей ролика и детали является постоянным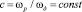 
;
откуда, при условии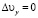 
, получим:
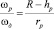(6)
В этой зависимости левая часть является постоянной величиной, в то время как правая часть переменна в связи с тем, что текущая глубина внедрения ролика в деталь по лини максимального нагружения и радиус ролика меняются по длине контактной зоны. Проскальзывание будет отсутствовать в тех сечениях ролика, для которых уравнение (6) превратится в тождество. Формула (6) является основой для разработки методики экспериментальных исследований проскальзывания вызванного изменением радиуса ролика по длине контактной зоны и при угле самозатягивания равном нулю. Для конического ролика, часто применяемого на практике, в инструментах работающих по принципу самозатягивания зависимость изменения радиуса ролика и глубины внедрения имеют вид: на заходном участке
; 
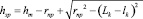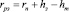, (7)
на участке сбега
; 
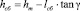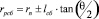; (8)
где hm – максимальная глубина внедрения ролика в обрабатываемую деталь, rпр – заходный радиус ролика, Lk, lk – длина контактной зоны и ее текущее значение, θ – угол конуса ролика.
Подставив представленные зависимости в формулу (6) получим уравнение для определения значения длины контактной, в котором отсутствует проскальзывание. Для этого, кроме того, необходимо измерить точное значение
На основании формул (3) построены графики зависимости проскальзывания от угла самозатягивания (рис. 2), из которых следует, что наибольшей по абсолютной величине проекцией проскальзывания является осевая составляющая (рис. 2). Из формул (3) при α = φ = 0 следует, что осевая составляющая ∆υx равна нулю, что очевидно. При увеличении угла самозатягивания составляющие ∆υy и ∆υz увеличиваются, причем при угле самозатягивания равном 90°, составляющая ∆υх становится касательной составляющей ∆υy (обе равны линейной скорости вращения детали). Составляющие ∆υz и ∆υy вектора проскальзывания зависят, кроме того, от длины контакта и радиуса ролика. С увеличением длины контактной зоны проскальзывание ∆υz увеличивается, а ∆υx – почти не меняется.
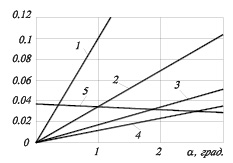
Рис. 2. Зависимость проскальзывания от угла самозатягивания: 1 – для ∆υx; 2,3,4 – для ∆υz; 5 – для ∆υy; R = 25 мм; ωр = 1 с-1; 2,5 – l = 10 мм; 3 – l = 5 мм; 4 – l= 3 мм
Полагая в формулах (3) α = 0, γ ≠ 0, получим:
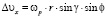(9)
Однако следует, что с увеличением углов γ и φ осевое проскальзывание ∆υх возрастает, при этом возникает усилие самозатягивания, действующее на инструмент. Это объясняет обнаруженное Шнейдером [1] явление: при увеличении угла конусности роликов свыше 4°…5° возможно возникновение самозатягивания инструмента за счет возрастания проскальзывания роликов. Следует, однако, отметить, что при условии (6) проскальзывание на фронтальной поверхности ролика направлено в сторону подачи, а проскальзывание на противоположной поверхности, т.е. на поверхности сбега, – в другую сторону. Тем не менее, суммарное усилие проскальзывания будет направлено в сторону подачи, так как нагружение ролика на фронтальной поверхности больше.
Проскальзывание между поверхностью ролика по характеру физико-механического воздействия на обрабатываемую поверхность аналогично процессу выглаживания. Следует ожидать, что с увеличением угла самозатягивания будет уменьшаться шероховатость обработанной поверхности, что и наблюдается при проведении экспериментальных исследований.
Библиографическая ссылка
Вирт А.Э., Отений Я.Н. МЕТОДИКА ОПРЕДЕЛЕНИЯ ПРОСКАЛЬЗЫВАНИЯ РОЛИКА ПРИ ППД // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 12-1. – С. 15-18;URL: https://applied-research.ru/ru/article/view?id=6250 (дата обращения: 23.11.2024).