Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Петрушева Н.А. 1

---

1 ФГБОУ ВПО «Сибирский государственный технологический университет»

Данная работа является продолжение исследований процесса производства трудновоспламеняемых древесноволокнистых плит мокрым способом. Ранее были установлены зависимости параметров горючести готовой древесноволокнистой плиты от зернового состава и массовой доли вспученного вермикулита; разработаны математические модели, адекватно описывающие процесс получения древесноволокнистых полуфабрикатов в производстве трудновоспламеняемых древесноволокнистых плит; определены оптимальные технологические режимы процесса размола древесноволокнистой массы, применение которых приводит к получению трудновоспламеняемых древесноволокнистых плит с необходимыми физико-механическими характеристиками; на основании результатов исследований была разработана композиция для получения трудновоспламеняемых древесноволокнистых плит мокрым способом. Однако вопросам энергопотребления не было уделено внимания. В данной работе с помощью методов математического моделирования и планирования эксперимента определены затраты электроэнергии на размол древесноволокнистой массы в производстве трудновоспламеняемых древесноволокнистых плит.

Статья в формате PDF

1035 KB

пожарная опасность

энергопотребление

древесноволокнистая плита

размол

дефибратор

рафинатор

1. Бекетов В.Д. Повышение эффективности производства древесноволокнистых плит [Текст] / В.Д. Бекетов. – М.: Лесн. пром-сть, 1988. – 160 с.

2. Пижурин А.А. Моделирование и оптимизация процессов деревообработки [Текст]: учебник / А.А. Пижурин, А.Н. Пижурин. – М.: МГУЛ, 2004. – 375 с.

3. Чистова Н.Г. Размол древесноволокнистой массы на промышленных установках при производстве ДВП [Текст]: дис. … канд. техн. наук: 05.21.03: защищена 20.12.2000 / Н.Г. Чистова. – Красноярск, 2000. – 170 с.

4. Чистова Н.Г. Переработка древесных отходов в технологическом процессе получения древесноволокнистых плит [Текст]: дис. … докт. техн. наук / Н.Г. Чистова. – Красноярск, 2010. – 415 с.

5. Солечник Н.Я. Производство древесноволокнистых плит [Текст] / Н.Я. Солечник. – М.: Гослесбумиздат, 1963. – 337 с.

6. Набиева А.А. Оценка влияния и совершенствование основных технологических параметров ножевых размалывающих машин [Текст]: дис. … канд. техн. наук: 05.21.03: защищена 24.09.04 / А.А. Набиева. – Красноярск, 2004. – 182 с.

7. Пижурин А.Н. Исследование процессов деревообработки [Текст] / А.Н. Пижурин, М.С. Розенблит. – М.: Лесн. пром-сть, 1984. – 200 с.

8. Антонов А.В. Размол древесноволокнистых полуфабрикатов при производстве трудновоспламеняемых древесноволокнисты плит / А.В. Антонов, Н.А. Петрушева, Ю.Д. Алашкевич, А.П. Чижов // Химия растительного сырья – 2012. – № 4. – С. 215–219.

Известно, что в производстве древесноволокнистых плит предварительная подготовка полуфабриката потребляет до 65 % всех затрат электроэнергии производства. На энергопотребление размольных машин при изготовлении древесноволокнистой массы, оказывают существенное влияние: концентрация массы, продолжительность работы размалывающих сегментов, зазор между ротором и статором, обороты подающего шнека дефибратора [1].

В связи с этим, целью данного исследования являлось установление зависимости удельного расхода электроэнергии от конструктивных параметров размалывающих машин и технологических характеристик процесса размола при производстве трудновоспламеняемых древесноволокнистых плит (ДВП).

Материалы и методы исследования

Наиболее предпочтительным для определения влияния основных конструктивных параметров размольного оборудования и технологических характристик процесса размола на физико-механические характеристики готовой древесноволокнистой плиты и для обеспечения достоверного математического описания объекта является многофакторный эксперимент, так как он позволяет при переходе к каждому последующему опыту варьировать все или почти все факторы одновременно.

В данной работе для построения математической модели процесса, проверки ее адекватности и для оценки влияния на процесс каждого управляемого фактора использован регрессионный анализ – метод, который позволяет устанавливать значения факторов и диапазоны их варьирования по своему усмотрению, не нарушая хода технологического процесса, согласно технических характеристик применяемого оборудования, требований стандартов к готовой продукции и т.п. [2].

Управляемые (входные) параметры выбирались нами исходя из анализа научных работ [3–6] показал, что наиболее сильное влияние на физико-механические характеристики готовых ДВП оказывают: на первой ступени размола (дефибратор) – износ сегментов, зазор между размалывающими дисками, скорость вращения нижнего шнека; на второй ступени размола (рафинатор) – износ сегментов, зазор между размалывающими дисками, концентрация древесноволокнистой массы.

При каждом изменении значений одного из управляемых факторов проводилось фиксирование затрат электроэнергии самописцами М-293, счетчиками МОD А4S и амперметрами, установленными на каждой машине.

Управляемые и контролируемые параметры многофакторного эксперимента представлены в табл. 1.

Таблица 1

Параметры многофакторного эксперимента

Значения уровней и интервалы варьирования факторов представлены в табл. 2.

Верхний, нижний и основной уровни варьирования фактора L/h соответствуют 90-, 10-, и 50- % износу сегментов гарнитуры размалываю-
щих машин.

К неконтролируемым факторам эксперимента относились не указанные выше геометрические и физико-механические характеристики процесса.

В результате статистической обработки полученных экспериментальных данных были получены следующие уравнения:

– для первой ступени размола

Yдеф = 210,3 + 6,78Х1 – 1,45Х2 + 5,15Х3 + 1,8Х12 – 1,5Х22 + 2,72Х32 – 5,97Х1Х2 + 3,24Х1Х3 + 4,63Х2Х3. (1)

– для второй ступени размола

Yраф = 274,4 + 2,16Х1 – 1,66Х2 + 1,41Х3 + 2,18Х12 – 1,96Х22 + 4,15Х32 – 2,02Х1Х2 – 1,325Х1Х3 + 2,55Х2Х3. (2)

Приведем некоторые общие выводы, касающиеся анализа и интерпретации полученных моделей. Для этого лучше всего пользоваться уравнениями в нормализованных обозначениях факторов. Поскольку представленные уравнения отличаются от линейных, то простое сравнение по абсолютной величине линейных коэффициентов регрессии не определяет относительную степень влияния факторов, поскольку присутствуют еще квадратичные члены и парные взаимодействия. Для квадратичной модели степень влияния фактора на изменение отклика не является постоянной. Она различна в разных точках диапазона варьирования, а при наличии парных взаимодействий определяется еще и уровнями факторов, входящих в эти взаимодействия [7].

Выборочный анализ уравнения (1) показал следующее. Влияние всех факторов на отклик является квадратичным, так как присутствуют
соответствующие квадратичные члены. При этом можно утверждать, что максимальное влияние на отклик оказывает фактор Х1, соответствующий износу сегментов размалывающей гарнитуры, так как именно для этого фактора ∂1max = 19,59. Однако при увеличении значений фактора Х1, отклик не всегда возрастает, иногда характер влияния меняется на противоположный. Оказывают влияние парные взаимодействия факторов.

Наглядное представление об эффекте парного взаимодействия даст анализ семейства графических зависимостей Yдеф от Х1 при различных значения Х3 и фиксированном уровне фактора Х2. Подставив значения Х2 = Х3 = + 1 в уравнение (1) получим

Yдеф = 219,85 + 4,05 Х1 + 1,8 Х12. (3)

Так как b11 = 1,8 > 0, то уравнение описывает вогнутую функция, то есть ветви параболы направлены вверх. Кроме того  = 4,05 > 2 = 3,6, следовательно вершина параболы находится вне диапазона варьирования фактора, а уравнение (3) описывает монотонно возрастающую функцию.

Для приближенного построения параболы воспользуемся пятью точками:

Х1  = – 1, Y = 217,6; Х1 = – 0.5, Y = 218,275; Х1 = 0, Y = 219,85; Х = 0.5, Y = 223,32; Х1 = 1, Y = 225,7 (верхняя кривая на рис. 1).

Сохранив значение Х2 = + 1 положим теперь в уравнении (1) Х3 = – 1. Получим зависимость

Yдеф = 200,29 – 2,46 Х1 + 1,8 Х12. (4)

По сравнению с уравнением (3) здесь изменился не только свободный член, но и коэффициент b1, который вместо значения 4,05 принял значение – 2,46. Это произошло из-за парного взаимодействия b13. В результате парабола, описываемая уравнением (4) становится монотонно убывающей с экстремумов вне диапазона варьирования. Это означает, что с увеличением фактора Х3, соответствующего скорости вращения нижнего шнека дефибратора, влияние износа сегментов (фактор Х1) на удельный расход электроэнергии увеличилось. В то же время значения удельного расхода электроэнергии возросли. Это следует из увеличения свободного члена в уравнении (3) по сравнению с (4) (нижняя кривая на рис. 1).

Аналогично можно проанализировать влияние остальных факторов и их парных взаимодействий на отклик.

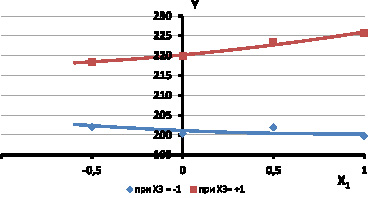
Рис. 1. Графики зависимостей Yдеф = f (Х1)

Анализ уравнения (2) показал следующее. Зависимость Y от каждого фактора является квадратичной, так как в уравнении (2) присутствуют соответствующие коэффициенты. Максимальное влияние на отклик оказывает фактор Х3, соответствующий концентрации массы в рафинаторе, так как ∂3max = 13,59. Также можно утверждать, что с ростом факторов Х1 и Х3 значения удельного расхода электроэнергии возрастают, а увеличение фактора Х2 позволяет снизить величину отклика.

Оценим влияние парных взаимодействий при помощи графических зависимостей. Подставив значения Х1 = Х2 = – 1 в уравнение (2) получим

Yраф = 272,1 + 0,185 Х3 + 4,15 Х12. (5)

Очевидно, что уравнение (5) описывает вогнутую функцию – b33 > 0, соотношение  = 0,185 < 2 = 8,3 позволяет сделать вывод о том, что экстремум функции (в данном случае минимум) находится в диапазоне варьирования. Для построения графика воспользуемся точками Х1 = – 1, Y = 276,1; Х1 = – 0.5, Y = 273,1; Х1 = 0, Y = 272,1; Х = 0.5, Y = 273,23; Х1 = 1, Y = 276,44 (нижняя кривая на рис. 2).

Оставив значение Х2 = – 1 примем Х1 = + 1, получим

Yраф = 280,46 + 2,635 Х3 + 4,15 Х12. (6)

Сравнивая уравнения (5) и (6) мы можем видеть, что значение свободного члена и коэффициента b3 увеличилось, парабола, описываемая уравнением (6) будет более крутой, экстремум функции сместится влево, к нижней границе интервала варьирования. таким образом проявилось влияние парного взаимодействия b13. Это означает, что с увеличением износа режущей гарнитуры влияние концентрации массы в рафинаторе на удельный расход электроэнергии увеличивается (верхняя кривая на рис. 2).

Анализируя графические зависимости на рис. 2 можно сделать следующие выводы. С ростом значений концентрации увеличивается удельный расход электроэнергии. При этом на начальной стадии обработки древесного волокна влияние увеличение концентрации приводит к незначительному снижению значений удельного расхода электроэнергии, затем значения отклика возрастают по мере возрастания фактора износа сегментов. Таким образом проявляется парное взаимодействие факторов Х1Х3 и их влияние на величину удельного расхода электроэнергии.

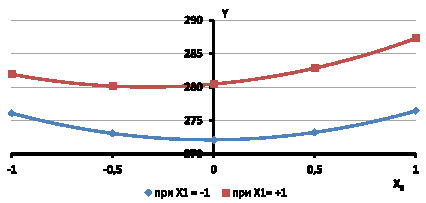
Рис. 2. Графики зависимостей Yраф = f (Х3)

Результаты исследования
и их обсуждение

В работе [8] были представлены результаты поиска оптимальных условий производства трудновоспламеняемых древесноволокнистых плит с целью установления таких технологических и конструктивных параметров размола древесноволокнистого полуфабриката, которые бы обеспечили максимальное удержание частиц вспученного вермикулита в древесноволокнистой композиции. В результате решения поставленной задачи были получены следующие значения технологических и конструктивных параметров дефибратора и рафинатора, обеспечивающих оптимальные условия размола при производстве трудновоспламеняемых древесноволокнистых плит мокрым способом.

Для размола технологической щепы в дефибраторе: L/h = 6 (50 %), z = 0,15 мм, n = 12 об/мин. Для размола древесноволокнистой массы в рафинаторе: L/h = 6 (50 %), z = 0,15 мм, с = 3,5 %. Найденные режимные параметры обеспечивают получение трудновоспламеняемых древесноволокнистых плит с массовой долей вспученного вермикулита ωв = 30 %. Однако, в указанной работе не учитывалось энергопотребление процесса размола.

Полученные в данной работе уравнения позволят определить удельный расход электроэнергии при оптимальных режимах процесса размола в производстве трудновоспламеняемых ДВП. Подставляя указанные значения в уравнения с натуральными обозначениями факторов получим Еуддеф = 199,9 кВт·ч/т; Еудраф = 279,9 кВт·ч/т, что в среднем на 7 % ниже производственных значений удельного расхода электроэнергии.

Выводы

Таким образом, полученные в ходе исследования зависимости позволяют, варьируя конструктивными параметрами размалывающих машин и технологическими характеристиками процесса размола древесноволокнистой массы, не только получить древесноволокнистые плиты с заданными свойствами, но и сократить расход электроэнергии на производство в среднем на 7 %.

Библиографическая ссылка