Вселенная в Эмпирической Теории Вселенной (ЭТВ) [1–4] представляет собой внутренность «черной дыры». Это стационарная, замкнутая, однородная и изотропная «частица», границы которой расширяются от момента возникновения и до наших дней со скоростью света (С), так как скорость волн не зависит от систем отсчета. Пространство также представляет собой волну, но уже гравитационную. Скорость гравитационной волны вычислена, она существенно меньше скорости света, но именно такая разница в скоростях двух фундаментальных взаимодействий (других взаимодействий в ЭТВ нет) обеспечивает наблюдаемую структуру Вселенной. Еще одна (в дополнение к гравитационной константе И. Ньютона), «вихревая» гравитационная константа связывает массу космического тела с волновым стационарным пространством вокруг него.
ЭТВ удовлетворяет:
● идее близкодействия (имеет собственный набор констант: GN – гравитационная константа И. Ньютона, GK – «вихревая» гравитационная константа, Vg – скорость гравитона);
● квантовым идеям (M/GK = λo – основная волна стационарного потенциала, «квантовые числа» и «спин»);
● релятивизму (константа K = C/Vg определяет структуру Вселенной).
При этом ЭТВ не дает расходимости в начальный момент времени (из-за связи пространства с массой: нет массы – нет пространства, и наоборот), и нет расходимости потенциала из-за ограниченности Вселенной и ее расширения.
Поскольку пространство представляет собой гравитационную волну, то силы для описания результатов взаимодействия не пригодны. Расширение Вселенной также невозможно описать с помощью сил, но в волновой механике расширение Вселенной и каждого космического тела и пространства легко объяснимо, а также легко решается задача многих тел.
Если Вселенная расширяется с постоянной скоростью – скоростью света, то любой линейный размер такой Вселенной также расширяется с постоянной скоростью пропорциональной линейному размеру Вселенной. Например, скорость удаления Луны от Земли равно DRE – M при расстоянии между ними RE – M, тогда возраст Солнечной системы равен: to = RE – M/DRE – M =10,1 млрд. лет. Если разделить радиус орбиты планеты, радиус планеты или массу планеты на возраст Солнечной системы, то получится прирост соответствующего параметра.
Рост линейных размеров тел и пространства, линейный рост массы тел приводит к изменению плотности тел и излучения в зависимости от радиуса тела ρ ~ M/r3 ~ r–2 или с учетом линейного расширения к зависимости от возраста ρ ~ t–2. Эти универсальные единицы измерения позволяют по параметрам Венеры, Земли и Марса находить такие зависимости параметров планет от единиц R–2 (r–2 или t–2), которые можно преобразовать в законы эволюции параметров каждой планеты (то есть в зависимость параметров от времени t для каждой планеты). Универсальность относительной единицы R–2 (r–2 или t–2) состоит в том, что она позволяет сравнивать планеты между собой в сопоставимых единицах и отслеживать эволюцию каждой из них, и всё это делать с помощью одного рисунка.
Цель данной работы состоит в анализе наблюдаемых гипсометрических распределений Венеры, Земли и Марса, и в поиске законов наблюдаемых параметров с позиций ЭТВ и с помощью метода наименьших квадратов.
Воспользуемся наблюдаемыми гипсометрическими кривыми для Венеры [5], Земли [6] и Марса [7]. Кривые приведены в том виде, как они представлены в указанных статьях на рис. 1.
Распределение высот поверхности по планете косвенно говорит о характере ее геологического строения. На Земле и Марсе это распределение явно бимодальное – есть два максимума распространенности, отражающие деление поверхности планеты на выступы материков и океанические бассейны. На Венере поверхность рассекается протяженными (тысячи километров), сложно построенными желобами, образованными роями тектонических разломов. По топографии и морфологии они похожи на так называемые рифтовые зоны Земли и, видимо, имеют ту же природу.
В [5] площадь ниже отметки высот – «0» составляет не более 10 % полной поверхности планеты Венера. Воспользуемся работой [6] (распределение Вейбулла с параметром α = 2) и подгоним распределения высот для материков (90 %) и океанической коры (10 %). Результаты подгонки приведены на рис. 2 (параметры β1 = β2 = 0,6, H1 = 0,7 км, H2 = 0,2 км, смещение между распределениями DH = H1 – H2 = 0,5 км).
Полученные распределения выглядят достаточно правдоподобно, то есть бимодальность возможно присутствует и выражена слабо. Глубина «океанической впадины» в области рифтовой зоны составляет приближённо 0,5 км, что говорит о самом начале зарождения океанической коры (видно только склоны материковой коры прорезанной не на всю толщину). Если возраст Солнечной системы составляет to = 10,1 млрд лет, то прирост радиуса Венеры составит DrV = rV/to 0,605 мм/год [4]. С таким приростом радиуса планеты площадь в 10 % (океаническая кора) нарастёт за 0,5 млрд лет. Этому возрасту соответствовала температура поверхности планеты равная T0,5 = 560 C, что меньше предполагаемой температуры плавления гранита. Если бы кристаллизация коры произошла при предполагаемой температуре плавления гранита, которой Венера достигла 2,2 млрд лет назад, то к настоящему времени площадь океанической коры составила бы 41 % и гипсометрическая кривая имела бы ярко выраженную бимодальность. Такого разнобоя можно избежать, если предположить, что материковая кора кристаллизовалась 2,2 млрд лет назад при температуре T2,2 = 950 С, а океаническая кора в настоящее время только начинает формироваться. Время в 2,2 млрд лет, по видимому, потребовалось для остывания планеты и наращивания определённой толщины коры, которая затем может «трескаться».
Если снова обратиться к рис. 1, то увидим, что ширина распределения увеличивается от Венеры к Марсу. Для количественной оценки DH проделаем процедуру подгонки распределений Вейбулла с параметром a = 2 для Земли и Марса, аналогично процедуре проделанной для Венеры. Результаты для указанных планет представлены на рис. 3 и 4.
В таблице сведены все расчётные параметры полученных распределений и возможные факторы, влияющие на приведённые параметры распределений.
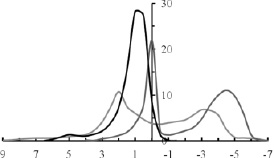
Рис. 1. Дифференциальные гипсометрические кривые: черная кривая – Венеры, темно-серая кривая – Земли и светло-серая кривая – Марса
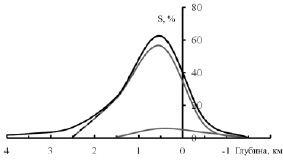
Рис. 2. Дифференциальная гипсометрическая кривая Венеры. Черная сплошная линия – наблюдаемая кривая высот, черная пунктирная линия – суммарная расчетная кривая высот, высокая серая сплошная линия – высоты на материке, низкая серая сплошная линия – глубины океанической коры
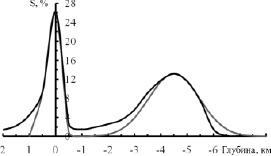
Рис. 3. Дифференциальная гипсометрическая кривая Земли. Черная сплошная линия – наблюдаемая кривая высот, серая сплошная линия – суммарная расчетная кривая высот
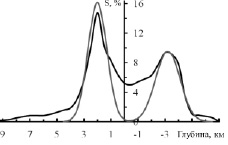
Рис. 4. Дифференциальная гипсометрическая кривая Марса. Черная сплошная линия – наблюдаемая кривая высот, серая сплошная линия – суммарная расчетная кривая высот
Расчетные параметры дифференциальных гипсометрических кривых Венеры, Земли и Марса
|
параметр |
планета |
||
|
Венера |
Земля |
Марс |
|
|
β1 |
0,6 |
0,24 |
0,7 |
|
β2 |
0,6 |
0,96 |
0,9 |
|
H1, км |
0,7 |
0,13 |
2,0 |
|
H2, км |
0,2 |
– 4,5 |
– 3,2 |
|
DH, км |
0,5 |
4,63 |
5,2 |
|
S∙Dr2 |
36,6 |
19,1 |
7,9 |
|
Sниз |
100 |
48 |
68 |
|
T, K |
753 |
288 |
208 |
|
Прирост радиуса планеты Dr, мм/год |
0,605 |
0,63 |
0,34 |
|
Dr2 |
0,366 |
0,397 |
0,116 |
|
Радиус орбиты планеты R, ∙108 км |
1,082 |
1,496 |
2,279 |
|
R2, ∙1016 км2 |
1,171 |
2,238 |
5,194 |
|
R–2 |
0,854 |
0,447 |
0,1925 |
|
Расчет по DH = 7,0707 – – 0,0087∙T, км |
0,52 |
4,57 |
5,26 |
Среди приведённых в таблице параметров распределений и возможных факторов, влияющих на них, просматривается, например, связь расстояния между максимумами распределений материка и океанической коры DH = H1 – H2 с температурой планеты.
На рис. 5 (и в таблице) представлены исходные данные расстояний между максимумами распределений материка и океанической коры DH рассмотренных планет, форма связи с температурой планеты, численные значения параметров регрессии и результаты расчета по регрессии. Коэффициент детерминации полученной регрессии достаточно высок R2 = 99,94 % чтобы, считать полученную регрессию эмпирическим законом. Следует обратить внимание, что температура, при которой регрессия пересекает ось X, равна T = 813K (рис. 5) и существенно зависит от точки Венеры. Точка Венеры в свою очередь определена весьма неуверенно, так как Венера находится в самом начале формирования океанической коры.

Рис. 5. Зависимость расстояния между максимумами распределений ∆H от температуры планеты
Анализ гипсометрических дифференциальных распределений Венеры, Земли и Марса показал, что распределение Вейбулла хуже описывает наблюдение в направлении от Венеры к Марсу, то есть по мере роста доли океанической коры. Критерий DH относится к вероятностным распределениям, поэтому пригоден при условии DH > (β1 + β2)/2. В случае с Венерой приведенный критерий не выполняется, поэтому желательно найти более надежные критерии для анализа и поиска закономерностей эволюции коры на планетах земной группы.
Отличие планет с атмосферами состоит в том, что они крупнее и расширяются с большей скоростью, из-за наличия атмосферы температура их поверхности эволюционирует быстрее, но температура распределена по поверхности достаточно равномерно, и они не имеют очень высокого градиента температур по терминатору.
Не смотря на то, что полученная регрессия прогнозирует образование рифтов практически сразу после образование твердой коры (что справедливо), датировки самых древних земных пород дают меньший возраст. Это еще один аргумент в пользу поиска иных критериев разграничения материковой и океанической коры.
В заключение следует обратить внимание на тенденции величин β1, β2 (таблица). На Земле много воды и очень большое различие β1 и β2. Из-за слабой атмосферы и большого радиуса орбиты Марс остывал быстро, поэтому β1 и β2 имеют большие значения. Кроме того, планета могла иметь океан, поэтому β2 для Марса близка значению для Земли.
Библиографическая ссылка
Курков А.А. АНАЛИЗ ГИПСОМЕТРИЧЕСКИХ РАСПРЕДЕЛЕНИЙ ВЕНЕРЫ, ЗЕМЛИ И МАРСА // Международный журнал прикладных и фундаментальных исследований. 2015. № 3-3. С. 395-399;URL: https://applied-research.ru/ru/article/view?id=6553 (дата обращения: 12.03.2026).

